экзамен математика. ответы. Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции
 Скачать 253.03 Kb. Скачать 253.03 Kb.
|
1 2 Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции. Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует. Производная - основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Дифференцирования суммы: Дифференцирования разности: Дифференцирования произведения (правило Лейбница): Дифференцирования частного: 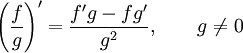 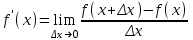  у уf(x) f(x0 +x) P f f(x0) M x 0 x0 x0 + x x Пусть f(x) определена на некотором промежутке (a, b). Тогда 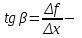 тангенс угла наклона секущей МР к графику функции. тангенс угла наклона секущей МР к графику функции.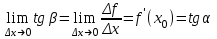 , ,где - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)). Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке. Уравнение касательной к кривой: 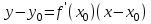 Уравнение нормали к кривой: 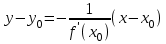 . .Производные основных элементарных функций. 1)С = 0; 9) 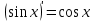 2)(xm) = mxm-1; 10) 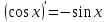 3) 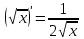 11) 11) 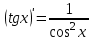 4) 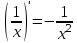 12) 12) 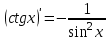 5) 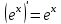 13) 13) 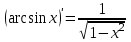 6) 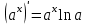 14) 14) 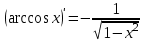 7) 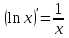 15) 15) 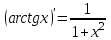 8) 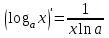 16) 16) 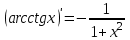 Дифференциал функции, его свойства. Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции. Обозначается dy или df(x). Из определения следует, что dy = f(x)x или dy = f(x)dx. Можно также записать: 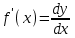 дифференциал функции f – это линейная функция y=f’(x0)*(x-x0) в точке x0 и обозначают df. Для функции x производная в каждой точке равна 1, то есть dx=x-x0 Поэтому пишут: df=f’(x)dx Дифференциал в математике — линейная часть приращения функции или отображения. Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом: f’(x)=df/dx Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на dx. Свойства 1) d(u ± v) = (u ± v)dx = udx ± vdx = du ± dv 2) d(uv) = (uv)dx = (uv + vu)dx = vdu + udv 3) d(Cu) = Cdu 4) Дифференцирование элементарных функций. Табличные производные. Дифференцирование элементарных функций (X+Y) ’=X’+Y’ (X-Y) ’=X’-Y’ (C*X) ’=C*X’, Где С это постоянная (X*Y) ’=X’Y+XY’ (X/Y) ’=( X’Y-XY’)/(Y*2) (F(K*X+B)) ’=KF’*(KX+B) ’ (F(g(X)) ’=F’(g(X))*g’ (x) Табличные производные C’=0, где С постоянная (Xn) ’=n*xn-1 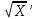 = =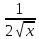 (ex)’=ex (Ax)’=Ax*ln g (Ln x)’= 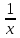 (sin x)’= cos x (Cos x)’= - sin x (Tg x)’= 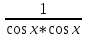 (Ctg x)’ = - 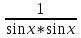 (Arcsin x) ’= 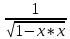 (Arcos x) ’= - 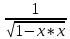 (Arctg x) ’= 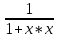 (Arcctg x) ’= - 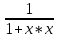 Неопределённый интеграл, его свойства. Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением. 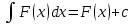 1* 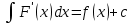 2* ( 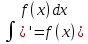 3* 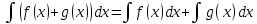 4* 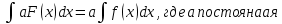 5* 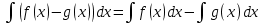 6* 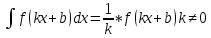 7* 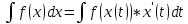 формула замены переменных формула замены переменных8* 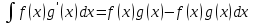 формула интегрирования по частям формула интегрирования по частямМетоды интегрирования: метод непосредственного интегрирования и метод разложения. Табличные интегралы. Метод не посредственного интегрирования Базовый метод свойства 1* и 6* и табличные интегралы А. 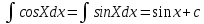 Б. 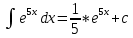 F(x)= 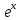 F(5x)= 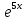 В. 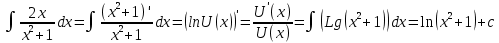 Метод разложения. База метода свойства 3*,4*,5*,6* и табличные интегралы. А. 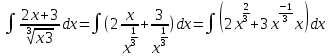 = ==2| 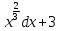 | |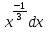 = = 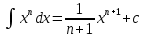 Табличные интегралы 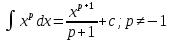 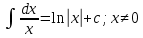 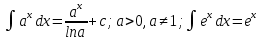 dx= dx=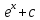 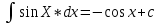 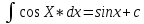 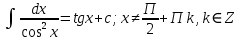 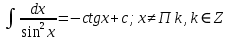 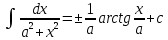 ; a ; a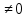 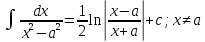 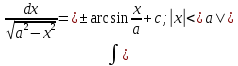 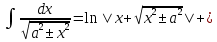 C CМетод интегрирования по частям и метод замены переменной под знаком интеграла. 7* 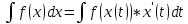 формула замены переменных формула замены переменных8* 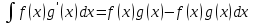 формула интегрирования по частям формула интегрирования по частямМетод замены переменных Теорема: Если требуется найти интеграл 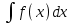 , но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается: , но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается: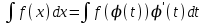 Пример. Найти неопределенный интеграл 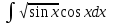 . .Сделаем замену t = sinx, dt = cosxdt. 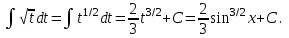 Пример. 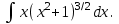 Замена 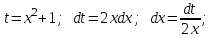 Получаем: Получаем: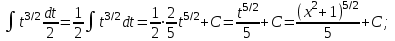 Интегрирование по частям. Способ основан на известной формуле производной произведения: (uv) = uv + vu где u и v – некоторые функции от х. В дифференциальной форме: d(uv) = udv + vdu Проинтегрировав, получаем: 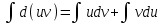 , а в соответствии с приведенными выше свойствами неопределенного интеграла: , а в соответствии с приведенными выше свойствами неопределенного интеграла: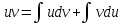 или или 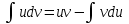 ; ;Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций. Пример. 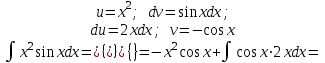 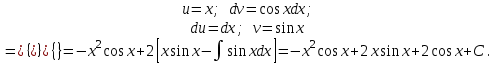 Пример.  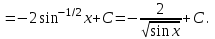 Пример. 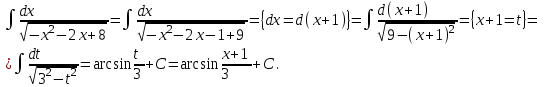 Понятие матрицы. Операции над матрицами, их свойства. Матрица размером MxN называется совокупностью M и N чисел, расположенных в виде прямоугольных таблиц из M строк и N столбцов Элементом матрицы (i и j) называется число расположенное на пересечении итой строки и джитого столбца матрицы Операции над матрицами А.Сложение матриц Это сумма матриц А и В одинакового размера MxN, называется квадратные матрицы MxN, которые определяются по формуле Сij=Aij+Bij 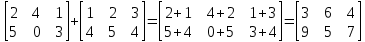 Б. умножение матриц Произведение матрицы А размера М и Х называется матрица В размерами М и Х, такая что Вij=P*aij, где Р это любое число. 5* 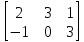 = =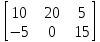 В. Вычитание матриц Разность А-В матриц элементами ij одинакового размера M и X называется матрица С размерами М и Х такая что Cij=Aij-Bij 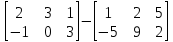 = =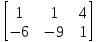 Г. Произведение матриц Необходимое условие: количество столбцов матрица А равно количеству строк матрицы В. Произведение матрицы А размерами М х К на матрицу В размерами К и N называется матрица С размерами М и К. такая что Cij=Ai1*B1j+Ai2*B2j+Ai3*B3j…+Aik*Bkj Примеры 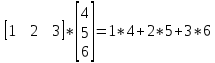 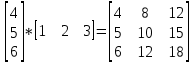 A*B= 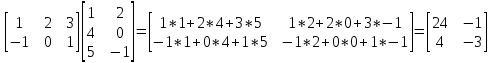 B*A= 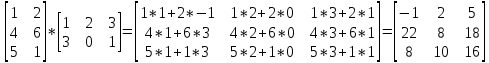 Свойства 1.) Сложение и вычитание допускается только для матриц одинакового размера. 2.) Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть A + Θ = A 3.) Все элементы нулевой матрицы равны нулю. 4.) Возводить в степень можно только квадратные матрицы. 5.) Ассоциативность сложения: A + (B + C) = (A + B) + C. 6.) Коммутативность сложения: A + B = B + A. 7.) Ассоциативность умножения: A(BC) = (AB)C. 8.) Дистрибутивность умножения относительно сложения: A(B + C) = AB + AC; (B + C)A = BA + CA. 9.) Свойства операции транспонирования матриц: (AT)T = A (AB)T = BTAT (A − 1)T = (AT) − 1, если обратная матрица A - 1 существует. (A + B)T = AT + BT detA = detAT 10.) Умножение матриц не коммутативно, т.е. АВ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными 11.) Если произведение АВ определено, то для любого числа верно соотношение: (AB) = (A)B = A(B). Квадратная матрица. Треугольная, диагональная, единичная матрицы. Степень квадратной матрицы. Матричный многочлен. Квадратной матрицей называется матрица у которой количество строк совпадает с количеством строк. Порядок квадратной матрицей называется количество её строк. Диагональю квадратной матрицы порядка n называется совокупность её элементов aii где i=j Побочной диагональю матрицы называется (a(n,1), a(n-1,2), … , a(1, n) ) Диагональная матрица называется квадратные матрицы у которой все элементы расположенные в не главной диагонали равны нулю Единичная матрица называется диагональная матрица у которой все элементы главной диагонали равны 1 и обозначается Е Пусть М принадлежит N и М не равно 1 М - ой степенью матрица А называют М – кратное произведение этой матрица АМ=А1*А2*…*АМ Свойства Am=Am-1*A=A*Am-1 Am*Ak=Ak*Am=Ak+m 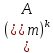 Матричный многочлен Пусть f(x)=a0xn+a1xn-1+…+an-1x+an A – квадратная матрица порядка М F(a)= a0An+a1An-1+…+an-1A+anE Где Е единичная матрица порядка М Называется матричный многочлен степени М Для любой квадратной матрицы А определено произведение А*А. Назовем произведение А*А квадратом матрицы А: A2 = A*A. Произведение A*Ar-1 для любого целого положительного числа r называется r-й степенью матрицы А. Т.е. Ar=A*Ar-1. Обозначаем Ar. Определитель квадратной матрицы. Вычисление определителей второго и третьего порядков. Определителем квадратной матрицы А порядка n называется алгебраическая сумма n! произведения вида (-1)n(a) a1j1 a2j2 …anjn в каждом из которых содержится по 1 – ому элементу из каждой строки и каждого столбца. Вычисление по любой строке и любому столбцу Вычисление треугольником Правилом дополнения Свойства определителей. Если все элементы некоторой строки или столбца равны 0, то определитель равен 0 Если определитель имеет 2 одинаковых строки или 2 одинаковых столбца, то он равен 0 Если элементы 2 строк пропорциональны то определитель равен 0 (Линейная зависимость строк и столбцов) Если все элементы К ого столбца определителя N порядка имеют вид Aij=L1*ai1+L2*ai2+…+Lk1*aik+Lk+1*aik+…+Ln*ain то определитель равен 0 Замечание: имеет место аналогичное свойство для строк 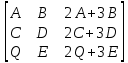 =0 =0При транспортировании матриц определитель не меняется Общий множитель некоторой строки элементов выноситься за знак определителя При перестановке 2 ух строк или 2 ух столбцов определителя изменяется только знак Если в некоторой строке прибавить другую строку умноженную на произвольные числа то определитель не измениться Если к некоторому столбцу прибавить другой столбец умноженный на любое число то определитель не изменится Если все элементы К ого столбца определителя Д n-ого порядка приставить в виде Aij=L1Bi1+L2bi2 , то Д=L1Д1+L2Д2 Определитель Д ого порядка равен сумме по парных произведений всех элементов I ой строки, на их алгебраические дополнения Определитель треугольной и диагональной матрицы равен произведению всех её элементов главной диагонали det A = det AT; det ( A B) = det A det B. det (AB) = detAdetB Общие способы вычисления определителей. Приведение к треугольному виду; свойства 6 и 8 Разложение определителя по строке; свойство 10 Разложение определителя по столбцу; свойство 11 Представление определителя в виде суммы определителей Метод рекурертных соотношений Теорема Лапаса Ранг матрицы, его свойства. Методы нахождения ранга матрицы. Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s. Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается Rang А. Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк. Методы нахождения ранга матрицы нахождение ненулевых строк. По нахождению базисного минора. Обратная матрица. Теорема о существовании обратной матрицы. Методы нахождения обратной матрицы. Определим операцию деления матриц как операцию, обратную умножению. Определение. Если существуют квадратные матрицы Х и А, удовлетворяющие условию: XA = AX = E, где Е - единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается А-1. Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну. Рассмотрим общий подход к нахождению обратной матрицы. Исходя из определения произведения матриц, можно записать: AX = E 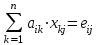 , i=(1,n), j=(1,n), , i=(1,n), j=(1,n), Пример. Дана матрица А = 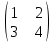 , найти А-1. , найти А-1. 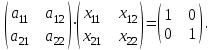 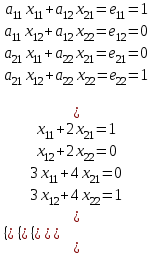 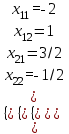 Таким образом, А-1= 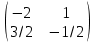 . .Для нахождения обратных матриц больших порядков, применяют следующую формулу: 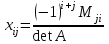 где Мji- дополнительный минор элемента аji матрицы А. Пример. Дана матрица А = 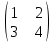 , найти А-1. det A = 4 - 6 = -2. , найти А-1. det A = 4 - 6 = -2.M11=4; M12= 3; M21= 2; M22=1 x11= -2; x12= 1; x21= 3/2; x22= -1/2 Таким образом, А-1= 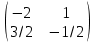 . .свойства 1) (A-1)-1 = A; 2) (AB)-1 = B-1A-1 3) (AT)-1 = (A-1)T. Собственные значения матрицы. Собственные и присоединённые векторы матрицы. Пусть А- квадратная матрица порядка n Определение 1. Комплексное число называется собственным значением матрицы А, если существует ненулевое решение матричного уравнения Алгебраическая кратность собственного значения лямбда матрицы А, называеться кратность коря лимба характеристического уравнением Det(A-גE) Квадратная матрица порядка n имеет с учетом кратности M собственных значений Собственный вектор квадратной матрица А называеться отвечающий её собственному значению лямбда, называеться не нулевое решение Ах=גх Собственные вектора квадратной матрицы отвечающие различным её собственным значениям называемых линейным Каждому собственному значению лямбда матрицы а отвечает m=n-rang(A-גE) линейно не зависимых собственных векторов Геометрическая кратность собственного значения лямбда квадратной матрицы А называется количество линейно не зависимых собственных векторов этой матрицы отвечают их собственному значению Лямбда Комплексные числа, их геометрическая интерпретация. Определение. Комплексным числом z называется выражение 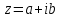 , где aи b – действительные числа, i – мнимая единица, которая определяется соотношением: , где aи b – действительные числа, i – мнимая единица, которая определяется соотношением: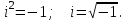 Определение. Числа 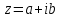 и и 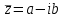 называются комплексно – сопряженными. называются комплексно – сопряженными.Определение. Два комплексных числа 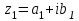 и и 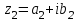 называются равными, если соответственно равны их действительные и мнимые части: называются равными, если соответственно равны их действительные и мнимые части: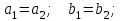 Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части. 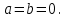 1) два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) называются равными, если x1 = x2 и y1 = y2; 2) суммой комплексных чисел z1 и z2 называется комплексное число z вида z = (x1 + x2, y1 + y2); 3) произведением комплексных чисел z1 и z2 называется комплексное число z = (x1x2 - y1y2, x1y2 + x2y1); 4) множество комплексных чисел Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2 + z = z1, откуда находим z = z1 - z2 = (x1 - x2, y1 - y2). Частным комплексных чисел z1 и z2 называется комплексное число z такое, что . Отсюда находим Z=( 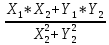 ; ;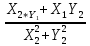 ) )Алгебраическая форма комплексного числа. Действия над комплексными числами. Z=x+yi алгебраическая форма Z=x-jy число сопряженное числу Z=x+yi j - мнимая единица j2=-1 1)Сложение и вычитание. 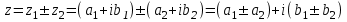 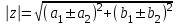 Умножение. 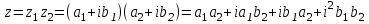 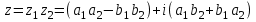 В тригонометрической форме: 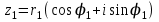 , , 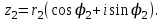 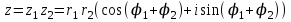 3) Деление. 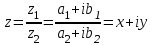 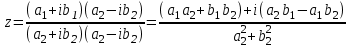 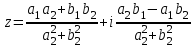 В тригонометрической форме: 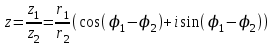 4) Возведение в степень. 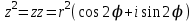 В общем случае получим: 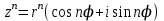 , ,5) Извлечение корня из комплексного числа. 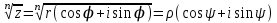 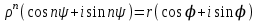 Отсюда: 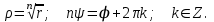 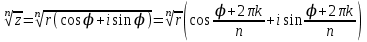 Модуль и аргумент комплексного числа. Главное значение аргумента. Тригонометрическая и показательная формы комплексного числа. Действия над комплексными числами в тригонометрической форме. Z=a+b A=(a,b) |Z|=r= 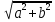 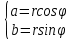 Z=r(cos 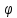 +sin +sin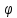 ) )ArgZ=h –аргумент комплексного числа - 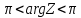 |Z|= 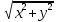 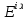 =cos =cos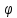 +sin +sin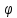 формула Эйлера формула Эйлераz 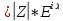 показатель формулы комплексного числа показатель формулы комплексного числа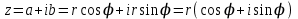 тригонометрической формой комплексного числа. тригонометрической формой комплексного числа.Пример: Z=4+3i X=4 y=3 >0. 2 четверть |Z|=sqrt(4*4+3*3)=sqrt25=5 Tga=y/x=3/4 a=arctg(3/4)+ПК argZ=arctg(3/4) Z=5*(cos(arctg(3/4))+isin(arctg(3/4))) –тригонометрическая форма. Z=5*e*arctg(3/4) – показательная форма. Действия 1) Умножение 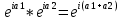 2) Деление 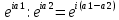 3)Введение в степень 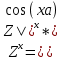 +isin(xa)) +isin(xa))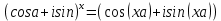 - формула Муавра - формула Муавра4) извлечение корня из n степени Корень n-ой степени из комплексного числа. Логарифм и степень комплексного числа. 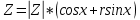 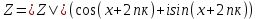 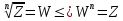 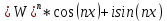 =|Z|*( =|Z|*(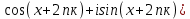 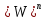 = =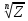 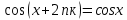 Sin(x+2пк)=sinx 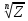 = =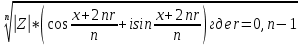 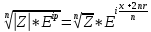 Приведём главное значение логарифма для некоторых аргументов: Правило Крамера. Решение линейных систем алгебраических уравнений. Если DetA не равен 0, то слау при условии n=m имеет единственное решение . X=DetA/Detb Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно) Пример. 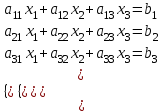 A = 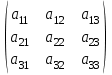 ; 1= ; 1= 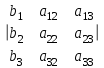 ; 2= ; 2= 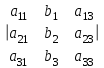 ; 3= ; 3= 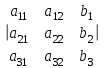 ; ;x1 = 1/detA; x2 = 2/detA; x3 = 3/detA; Системы линейных алгебраических уравнений. Общие понятия. Теорема Кронекера-Капелли. Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом: 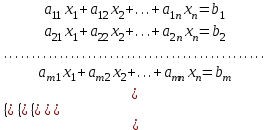 , (1) , (1)где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Ax=B Решением слау называется упорядоченный набор чисел х1 х2 х3 при постановке которых в уравнение системы каждый из этих выражений обращается в тождество Теорема Кронекера-Капелли: Неоднородная слау была совместна, необходима и достаточная, чтобы ранг основной матрицы был равен рангу расширенной матрицы этой систему. 1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга. 2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше. Однородные и неоднородные системы линейных алгебраических уравнений. Теоремы о существовании решений. Структура общего решения. Слау называется однородной если В1=В2=Вм=0 Ax=0 Слау называется не однородной если В1, B2, …, Bm не равно 0. Свойства однородной системы 1* любая однородная слау совместна, имеет решение X1=0 X2=0 Xn=0 2* любая линейная комбинация решений однородной слау является решение этой системы 3* однородная слау имеет не нулевое решение тогда и только тогда когда ранг матрицы её коэффициента меньше количества её неизвестных 4* однородная слау имеет только нулевое решение когда ранг коэффициента равен количеству не известных этой системы. Свойства неоднородной системы 1* разность 2-ух решений неоднородной слау является решение неоднородных систем равных. Ax=B Ay=B A(x-y)=Ax-Ay=B-B=0 U=x-y 2* общее решение совместных неоднородных систем общей слау представляет собой сумму некоторого решения этой системы и общего решения однородной системы х=y+-u’ 3* совместная неоднородная слау имеет единственное решение тогда и только тогда когда ранг матрицы коэффициентов равен рангу расширенной матрицы и это равно количеству неизвестных. 4* неоднородная слау имеет бесконечно много решений тогда и только тогда когда ранг расширенной матрицы меньше n Общим решением однородной слау называется, решение систем из которого может быть получено любое решение этой системы. Фундаментальной системой решений ФСР однородной слау называется максимальная совокупность своих линейно независимых решений. Если rang A=r n-количество неизвестных в однородной слау и r Общим решением системы алгебраических уравнений называется множество всех решений. Теорема: Если 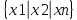 – ФСР однородных слау, то её общее решение Х слау предстоит виде – ФСР однородных слау, то её общее решение Х слау предстоит виде x= 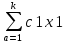 Системы координат на плоскости. Система координат на плоскости или в пространстве позволяет каждой точке сопоставить набор действительных чисел - ее координат. В результате геометрическая задача сводится к алгебраической задаче. На плоскости задаются декартова или криволинейная система координат. Декартова система координат может быть прямоугольной или косоугольной. Имеется множество криволинейных систем координат: полярная, биполярная, эллиптическая и другие Декартова система координат на плоскости Определение. Осью координат называется прямая, на которой заданы положительное направление, начало отсчета 0 и единичный отрезок Определение Декартовой системой координат на плоскости называется упорядоченная совокупность двух пересекающихся осей координат с общим началом О. Полярная система координат Определение Полярная система координат из точки О на плоскости, называется полюсом, луча, исходящего из полюса и единичного отрезка. Луч, исходящий из полюса, называется полярным лучом или полярной осью. Полярными координатам точки А на плоскости являются полярный радиус r и полярный угол Определение Полярным радиусом точки А называется расстояние от точки А до полюса. Определение Полярным углом точки А, называется величина ориентированного угла между полярным лучом ОР и углом ОА Прямая на плоскости. Различные уравнения прямой на плоскости Направляющий вектор прямой – это любой не нулевой вектор расположенный на этой прямой или прямой параллельной АВ=גa A(x0y0) В (x1y1) Нормальный вектор прямой это любой не нулевой вектор расположенный на прямой перпендикулярной данной прямой A(x-x0)+B(y-y0)=0 уравнение прямой с нормальным вектором проходящий через заданную точку М Ах+By+с=0 общее уравнение 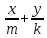 =1 уравнение прямой в отрезках =1 уравнение прямой в отрезках Xcosa+ysina-d=0 нормальное уравнение прямой Y=kx+ r уравнение прямой с угловым коэффициентом r=r0+ta параметрическое векторное направление прямой 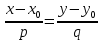 каноническое уравнение каноническое уравнение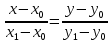 уравнение прямой проходящей через 2 точки уравнение прямой проходящей через 2 точкиУсловия пересечения, параллельности, совпадения и перпендикулярности двух прямых на плоскости. Определение угла между двумя прямыми. Ax+By+C=0 общее уравнение в декартовой системе Под углом между прямыми плоскости понимают наименьший из двух смежных углов, образованными этими прямыми. Если прямые А1 и А2 заданы уравнением с угловым коэффициентами y=k1x+b1 и y=k2x+b2, то угол 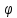 между ними вычисляется по формуле между ними вычисляется по формуле 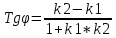 Условие параллельности прямых A1 и А2 имеет вид k1=k2 Условие перпендикулярности 1 и А2 имеет вид 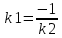 Если прямые заданы уравнением A1x+B1y+C=0 и A2x+B2y+C=0 то величина 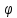 угла между ними вычисляется по формуле угла между ними вычисляется по формуле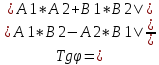 Условие параллельности прямых A1 и А2 имеет вид 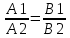 (или A1*B2 - A2*B1=0) (или A1*B2 - A2*B1=0)Условие перпендикулярности 1 и А2 имеет вид A1*A2+B1*B2=0 Расстояние d от точки М(Xo,Yo) до прямой Ax+By+C=0 Называеться длинна перпендикуляра опущенного из этой точки на прямую 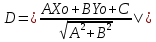 Расстояние от точки (Xo,Yo) до прямой Xcosa+ysina-p=0 D=|XoCosa+YoSina-p| Угол между плоскостями 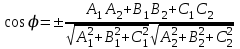 Уравнение кривой на плоскости. Кривые второго порядка на плоскости, их классификация. 1 2 |
