для замены. Илья Производные. Производные

• Название: Производные
• Анкор: для замены
• Дата: 24.06.2022
• Размер: 247.45 Kb.
• Имя файла: Илья Производные.docx
• Тип: Документы; #613924

Тема: Производные
Подготовил студент группы ЭМ 13-21

Тропин Илья

1. Определение производной, ее физический и геометрический смысл.

Рассмотрим функцию и ее график (Рис. 1). Для наглядности будем использовать физическую интерпретацию производной.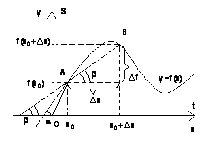



Рис. 1.
Аргументом пусть будет время^t. Зависимой переменной пусть будет^s – расстояние до дома. График функции показывает путь до дома в каждый момент времени.

x₀– момент времени. В этот момент времени мы находимся на расстоянии от дома.
Через некоторое время  мы будем находиться на расстоянии  от дома. Мы имеем приращение аргумента – , и приращение функции –  .

Получим треугольник, у которого катеты равны приращению аргумента, приращению функции, а гипотенуза АВ – секущая, где – тангенс угла наклона этой секущей.

Нас интересует отношение приращения функции к приращению аргумента.



Во-первых, мы получим среднюю скорость. Таков физический смысл.

А геометрический смысл состоит в том, что мы получим тангенс угла наклона секущей.

За конечное время  может произойти множество событий, и все их надо уловить, отразить. Для этого устремим  к 0. То есть мы будем рассматривать ближайшие точки к точке . Но если приращение аргумента стремится к 0, то приращение функции также стремится к 0. Тогда секущая АВ будет стремиться занять положение касательной к графику в точке А. Рассмотрим, что произойдет с отношением:



Более строгое определение
Такой предел называется производной функции и обозначается .


Каков физический и геометрический смысл производной?
– это мгновенная скорость в момент . Таков физический смысл производной.

Геометрический смысл: – тангенс угла наклона касательной в точке .


Мы вспомнили определение производной, ее физический и геометрический смысл.
Следующей нашей целью будет вспомнить технику дифференцирования, то есть технику нахождения производных.
2. Таблица производных
1.  (производная от постоянной величины является нулем)

Например:  , поскольку тангенс – величина постоянная и от ^x не зависит.

2. Следующая функция линейная:



То есть производной от линейной функции является ее угловой коэффициент.

Например:

1.

2.

3. 

4. 

5. 

6. 

7. 

8. 
3. Правила нахождения производных

1.

1) То есть производная суммы равна сумме производных

1. .

2.

2) То есть константу можно выносить за знак производной.

.

3) Производная произведения:





4) Производная частного:





4. Производные сложных функций





Тогда:

1.

а.

б.

2.

а.

б.

3.

а.

б.

4.

5.

а.

б.

6.

а.

б. 

Мы повторили определение производной и таблицу производной. Следующий урок посвятим исследованию функций с помощью производных.

Теория:

Задача 1 (о скорости движения). Материальная точка движется по прямой, на которой заданы начало отсчёта, единица измерения (метр) и направление. Закон движения задан формулой s=s(t) , где t — время (в секундах), s(t) — расстояние материальной точки от начала отсчёта (её координата) в момент времени t (в метрах). Найти скорость движения материальной точки в момент времени t (в м/с).

Решение. Пусть в момент времени t материальная точка была в положении T.



В момент времени t+Δt  материальная точка будет в точке K, то есть  

OK=s(t+Δt).

Значит, за Δt секунд материальная точка переместилось из T в точку K. Имеем:

TK=OK−OT=s(t+Δt)−s(t). Полученную разность мы назвали приращением функции: 

s(t+Δt)−s(t)=Δs. Итак, TK=Δs(м). Средняя скорость v_ср движения материальной точки за промежуток времени 

[t;t+Δt] равна v_ср =

А скорость v(t)  в момент времени t (мгновенная скорость) — это тоже скорость движения за промежуток времени [t;t+Δt], но Δt  выбирается очень маленьким, почти равным нулю, то есть Δt→0. Это значит, чтоv(t)=

Итак,



Задача 2 (о касательной к графику функции). На графике функции y=f(x) взяли точку M(a;f(a)) и в этой точке провели касательную к графику функции. Необходимо определить угловой коэффициент этой касательной.

Решение. Дадим аргументу приращение Δx и рассмотрим на графике точку P с абсциссой a+Δx. Ордината точки P равна f(a+Δx). Угловой коэффициент секущей MP равен тангенсу угла между секущей и осью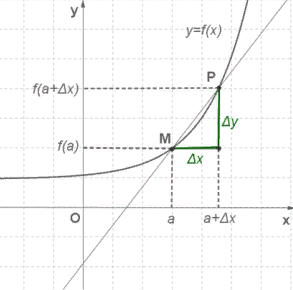



При Δx, стремящемся к нулю, точка P будет приближаться по графику к точке M. При этом касательная будет предельным положением секущей. Значит, угловой коэффициент касательной равен   . Используя приведённую выше формулу для k_сек, получаем:


Производные некоторых элементарных функций:

1.

2.

3.

4.

5.

6.

7.

8.

Доказательство формулы (√x)Ꞌ=1/(2√x)

Дано:

Доказать:

Доказательство

Изобразим график функции:  (см. Рис. 1). Зафиксируем точку x₀ и приращение Δx аргумента . Получаем новое значение аргумента x₀+Δx и, соответственно, новое значение функции f(x₀+Δx). То есть при переходе от значения аргумента x₀ к x₀+Δx значения функции изменяются соответственно от f(x₀)  до f(x₀+Δx). Значение функции в новой точке равно .

Получили прямоугольный треугольник (выделен красным цветом), катетами которого являются два приращения – приращение аргумента (Δx) и приращение функции (Δf) – разность между значением функции в новой точке и значением функции в старой точке).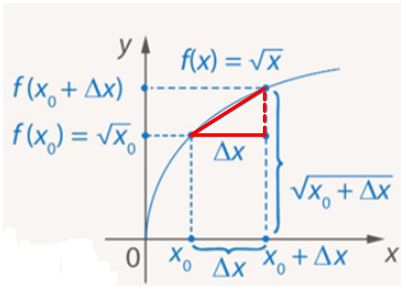





Найдём отношение :



Умножим числитель и знаменатель на выражение



В числителе получили выражение разности квадратов:



Следовательно:



Проанализируем данное выражение при :



x₀ – произвольное допустимое число, поэтому: