Промежуточная аттестация по алгебре 8. алг 8 +. Промежуточная аттестация по алгебре (тестирование) 8 класс
 Скачать 247.74 Kb.
|
|
Промежуточная аттестация по алгебре (тестирование) 8 класс Спецификацияконтрольных измерительных материалов для проведения промежуточной аттестации по АЛГЕБРЕ Назначение КИМ – оценить уровень общеобразовательной подготовки по алгебре обучающихся VIII классов общеобразовательных организаций. Документы, определяющие содержание КИМСодержание итоговой работы определяется на основе документов: - Федерального государственного образовательного стандарта основного общего образования, утвержденного приказом Министерства образования и науки РФ от 17.12.2010 г. № 1897 - Основной общеобразовательной программы основного общего образования МБОУ "Липовская средняя школа" - Математика. Программы 5-11кл. А.Г. Мерзляк. – М.: Вентана-Граф. 2018 Подходы к отбору содержания, разработке структуры КИМОтбор содержания, подлежащего проверке в тестировании, осуществляется в соответствии с обязательным минимумом содержания основных образовательных программ и требованиями к уровню подготовки выпускников Федерального государственного образовательного стандарта основного общего образования по алгебре. В каждый вариант КИМ включены задания, проверяющие уровень знания содержания всех основных разделов курса алгебры и выполнение основных требований к уровню подготовки обучающихся VIII класса. 4. Характеристика структуры и содержания КИМ Тестирование состоит из 13 заданий. Задания проверяют знания, составляющие основу алгебраической грамотности обучающихся, а также способность применить знания и умения в контекстах, соответствующих основным разделам курса. Аттестационное тестирование по алгебре в 8 классе содержит 2 варианта. Каждый вариант включает 13 заданий. Составлен из вопросов на уровне: часть 1 – вопросы 1-10 - базовый уровень (вопросы с одним правильным вариантом ответа), часть 2 – вопросы 11-13 задания повышенного уровня сложности (на установление соответствия, причинно-следственных связей, построить график, составление математической модели текстовой задачи и ее решение. 5. Распределение заданий КИМ по содержанию, проверяемым умениям и способам деятельностиРаспределение заданий по содержательным разделам курса алгебры показано в таблице 1.Распределение заданий тестирования по видам проверяемых умений и способам действий Таблица 1.Распределение заданий тестирования по содержательным разделам курса
6. Распределение заданий КИМ по уровням сложностиВ работе используются задания базового и повышенного уровней сложности. Распределение заданий КИМ по уровням сложности показано в таблице 2. Таблица 2. Распределение заданий тестирования по уровням сложности
7. Продолжительность тестирования по алгебреНа выполнение тестирования отводится 45 мин. 8. Дополнительные материалы и оборудование: линейка, таблица квадратов двузначных чисел.9. Система оценивания выполнения отдельных заданий и работы в целомКаждый правильный ответ заданий 1-10 оценивается в 1 балл. Задание 11 – 2 балла (нет ошибок- 2 балла, одна ошибка- 1 балл) Задание 12 – 2 балла (1 балл- верно построены графики, по 1 балл верное решение) Задание 13- 2 балла (1 б- составлена математическая модель, выполнена работа с математической моделью, но есть одна вычислительная ошибка , 0 б- две ошибки и более) Итого – 16 баллов Критерии оценок: «2»: ученик набрал менее 8 баллов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Код раздела | Код элемента | Элементы содержания, проверяемые в ходе промежуточной итоговой аттестации |
| 1 | | Рациональные выражения |
| 1.1. | Рациональные дроби. Основные понятия | |
| 1.1.1 | Основное свойство рациональной дроби дроби | |
| 1.1.2 | Сокращение рациональной дробей | |
| 1.1.3 | Сложение и вычитание рациональных дробей с разными знаменателями | |
| 1.1.4 | Умножение и деление рациональных дробей | |
| 1.1.5 | Рациональные уравнения | |
| 1.2 | Возведение рациональной дроби в степень | |
| 1.2.1 | Степень с отрицательным целым показателем | |
| | 1.2.2 | Функция  , её свойства и график |
| 2 | | Квадратные корни. Действительные числа |
| 2.1 | Функция  и её график | |
| 2.2 | Квадратные корни. Арифметический квадратный корень | |
| 2.3 | Множества | |
| 2.3.1 | Множества и его элементы | |
| 2.3.2 | Подмножество. Операции над множествами | |
| 2.3.3 | Числовые множества | |
| 2.4 | Свойства арифметических квадратных корней | |
| 2.4.1 | Тождественные преобразования выражений, содержащих арифметические корни | |
| 2.5 | Функция  и её график | |
| 3 | | Квадратные уравнения |
| 3.1 | Квадратное уравнение. Основные понятия | |
| 3.1.1 | Приведенное (неприведенное) квадратное уравнение | |
| 3.1.2 | Полное (неполное) квадратное уравнение | |
| 3.2 | Корень квадратного уравнения | |
| 3.2.1 | Дискриминант | |
| 3.2.2 | Формулы корней квадратного уравнения. | |
| 3.2.3 | Теорема Виета | |
| 3.2.4 | Квадратный трёхчлен | |
| 3.2.5 | Рациональные уравнения как математические модели реальных ситуаций. |
2.Перечень требований к уровню подготовки обучающихся 8 класса по Алгебре
В первых двух столбцах таблицы приведены коды требований, в третьем – требования к уровню подготовки обучающихся, соответствующие этим кодам.
| Код раз- дела | Код контро-лируемого требования (умения) | Требования (умения), проверяемые заданиями |
| 1 | Знать / понимать: | |
| 1.1 | существо понятия алгоритма; примеры алгоритмов; | |
| 1.2 | как используются математические формулы, уравнения ; примеры их применения при решении математических и практических задач | |
| 1.3 | вероятностный характер многих закономерностей окружающего мира | |
| 1.4 | смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации | |
| 1.5 | как потребности практики привели математическую науку к необходимости расширения понятия числа | |
| | 1.6 | Математические формулы, уравнения, теоремы |
| 2 | Уметь: | |
| 2.1 | оценивать значение квадратного корня из положительного целого числа | |
| 2.2 | распознавать рациональные и иррациональные числа | |
| 2.3 | выполнять преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем, степени с целым отрицательным показателем | |
| 2.4 | выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые | |
| 2.5 | использовать формулы сокращенного умножения (квадрат суммы, квадрат разности, разность квадратов) для упрощения вычислений значений выражений | |
| 2.6 | выполнять преобразования дробно-линейных выражений и выражений с квадратными корнями | |
| 2.7 | выполнять описание и построение графиков функций | |
| 2.8 | Определять координаты точки плоскости, строить точки с заданными координатами | |
| 2.9 | решать линейные и квадратные уравнения и неравенства | |
| 2.10 | решать систему уравнений аналитически и графически | |
| 2.11 | решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи | |
| | 2.12 | выполнять операции на множествах |
| 3 | Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: | |
| 3.1 | выполнения расчётов по формулам, составления формул, выражающих зависимости между реальными величинами | |
| 3.2 | описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций | |
| 3.3 | интерпретация графиков реальных зависимостей между величинами | |
Вариант 1.
Часть 1.
Найдите значение выражения
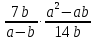при а = -13; b = 1,71) 7 2) -6,5 3) – 6 4) 0,3
2. Упростите выражение
и найдите его значение при а = -3. 1) -9; 2) 9; 3)
; 4)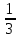 
.3. Упростить выражение:
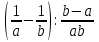.1) 1; 2) -ab; 3) ab.
4. Выберите неверное равенство:
1)
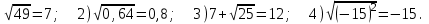
5. Между какими числами заключено число
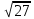
1) 2 и 3 2) 5 и 6 3) 12 и 14 4) 26 и 28
6. Решить уравнение
1) 6; 2) -6; 3) 6;-6; 4) 0;2.
7. Найти дискриминант квадратного уравнения
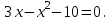
1) 49; 2) -31; 3) 119; 4) 36.
8. Найти множество, являющееся пересечением множеств А={1,2,5,7,10} и В={2,3,5,6,7,9}
1) С={2} 2) C={1,2,3,5,6,7,9,10} 3) C={3,6,9} 4) С={2,5,7}
9. Разложите на множители квадратный трёхчлен х2-х-30
1) (х-6)(х+5) 2) (х+6)(х-5) 3) разложить невозможно 4) (х+11)(х-11)
10. Найдите значение выражения
1) 220 2) 84 3) 200 4) 4
Часть 2.
11. Для каждой функции, заданной формулой укажите её график
Формула
А) y = х -1 Б) у = - х+1 В) у = - x2 + 1
График
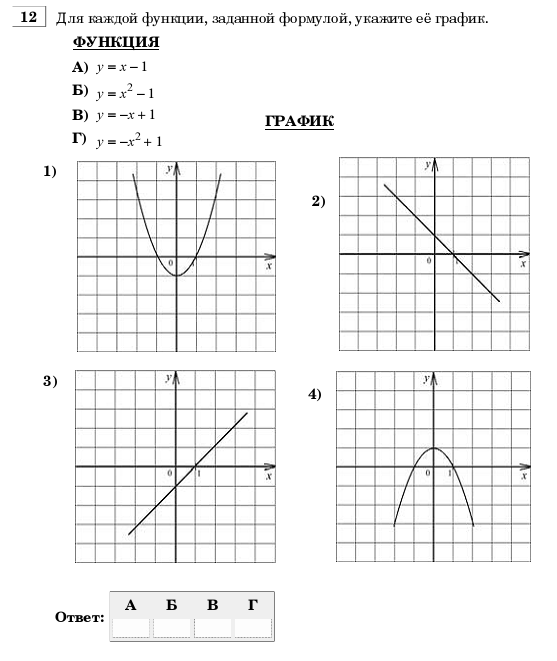
12. Решите графически систему уравнений:
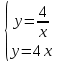
13. Моторная лодка прошла против течения реки 120 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Вариант 2.
Часть 1.
Найдите значение выражения
при а = 36; b = 2,21) 7,2 2) 3 3) – 3 4) 0,3
2. Упростите выражение
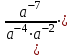и найдите его значение при 
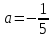.1) 5; 2) -5; 3)
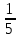; 4)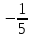 
.3. Упростить выражение:
.1) 15x; 2) 1,2; 3) 2x+1.
4. Выберите неверное неравенство:
1)
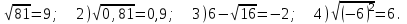
5. Между какими числами заключено число
1) 5 и 6 2) 2 и 3 3) 10 и 12 4) 27 и 29
6. Решить уравнение
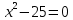.1) 5; 2) -5; 3) 5;-5; 4) 0;4.
7. Найти дискриминант квадратного уравнения
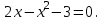
1) -8; 2) 16; 3) -23; 4) 24.
8. Найти множество, являющееся пересечением множеств А={1,2,5,7,10} и В={2,3,5,6,7,9}
1) С={2} 2) C={1,2,3,5,6,7,9,10} 3) C={3,6,9} 4) С={2,5,7}
9. Разложите на множители квадратный трёхчлен х2-х-30
1) (х-6)(х+5) 2) (х+6)(х-5) 3) разложить невозможно 4) (х+11)(х-11)
10. Найдите значение выражения
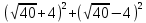
1) 40 2) 112 3) 4 4) 44
Часть 2.
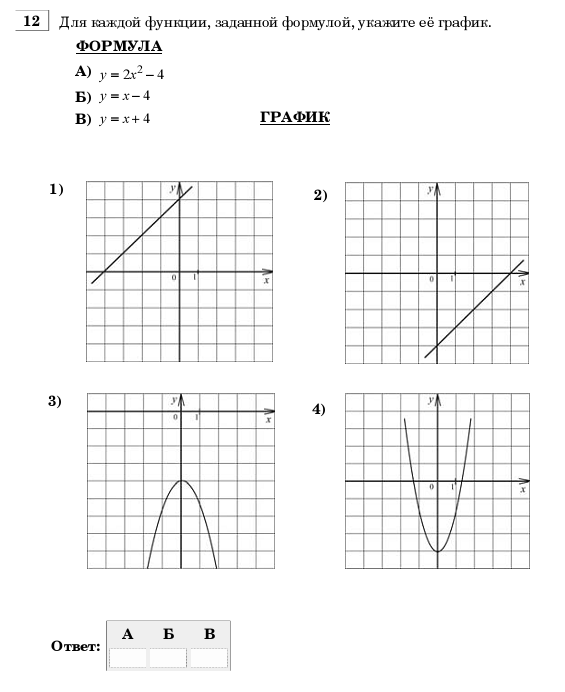
11. Для каждой функции, заданной формулой укажите её график
Формула
А) y = 2x2 – 4 Б) у = x – 4 В) у= х+4
График
12. Решите графически систему уравнений:
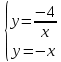
13. Моторная лодка прошла по течению реки 60 км и вернулась в пункт отправления, затратив на обратный путь на 1 часа больше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Ответы
Часть 1
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| В1 | 2 | 2 | 1 | 4 | 2 | 3 | 2 | 4 | 1 | 3 |
| В2 | 1 | 2 | 2 | 3 | 1 | 3 | 1 | 4 | 1 | 2 |
Часть 2
| | 11 | 12 |
| В1 | 324 | (1;4), (-1;-4) |
| В2 | 421 | (2;-2), (-2;2) |
| | 13 |
| В1 | 11 км/ч |
| В2 | 11 км/ч |