2_зертхана. Простые описательные статистики и распределения Основные статистики и таблицы

• Название: Простые описательные статистики и распределения Основные статистики и таблицы
• Дата: 12.12.2022
• Размер: 31.55 Kb.
• Имя файла: 2_зертхана.docx
• Тип: Документы; #841288

Простые описательные статистики и распределения

Основные статистики и таблицы включают процедуры вычисления среднего, стандартного отклонения, дисперсии, асимметрии и эксцесса выбранных переменных.

Среднее - это мера центрального положения (центра) непрерывного распределения.

Стандартное отклонение и дисперсия - это меры разброса или изменчивости значений относительно центра.

Асимметрия - это мера "скошенности" распределения.

Эксцесс - это мера "остроконечности" или "пикообразности" распределения, т.е. величины того, как распределение растягивается или скапливается вокруг среднего.

Основные статистики позволяют вычислить таблицы распределений частот и посмотреть распределения на гистограммах.

После вычисления описательных статистик вы можете построить распределение переменных с помощью щелчка мыши в таблице результатов.
Основные статистики и таблицы

Статистики, включенные в этот модуль, условно называются основными или описательными (дескриптивными) статистиками и рассматриваются в одной группе, т.к. обычно они используются совместно, особенно на начальной, разведочной стадии анализа данных.

Фактически эти статистики являются тестами, чрезвычайно полезные исследователю в самых разнообразных ситуациях.

Различные типы основных статистик и таблиц подробно описаны в последовательных справочных окнах.

Описательные статистики - Вводный обзор

Выберите эту процедуру для вычисления таких основных описательных статистик, как средние, медианы, стандартные отклонения и другие. Дополнительные описательные статистики (включая задаваемые пользователем процентили) можно вычислить в модуле Непараметрическая статистика.

Среднее

Среднее показывает центральное положение (центр) переменной и рассматривается совместно с доверительным интервалом. Обычно интерес представляют статистики (например, среднее), дающие информацию о популяции в целом. Чем больше размер выборки, тем более надежна оценка среднего. Чем больше изменчивость данных (больше разброс), тем оценка менее надежна (см. также Элементарные понятия статистики).

Среднее = (Sx_i)/n

где n число наблюдений (объем выборки).

Доверительный интервал для среднего

Доверительные интервалы для среднего задают область вокруг среднего, в которой с заданным уровнем доверия содержится "истинное" среднее популяции (см. также Элементарные понятия статистики). В Основных статистиках вы можете построить доверительные интервалы для любого p-уровня; например, если среднее в вашей выборке равно 23, а нижняя и верхняя границы для p=.05 равны 19 и 27 соответственно, то вы можете заключить, что с 95% вероятностью среднее выборки больше 19 и меньше 27.

Говоря более точно, если вы последовательно вычисляете этот по большому количеству независимых случайных выборок одинакового размера, то 95% этих интервалов будут, действительно, включать в себя истинные значения среднего, т. е. в 95% случаев вы окажетесь правы, утверждая, что истинное значение среднего содержится внутри данного доверительного интервала. Таким образом, выражаясь технически, значение 95% относится к процедуре построения статистического интервала, а не к самому наблюдаемому интервалу (см. работу Hahn & Meeker, 1991, стр. 31).

Если вы установите меньшее значение p-уровня, то интервал будет шире, и увеличится "уверенность" в оценке, и наоборот; как мы знаем из прогнозов погоды, чем "неопределеннее" прогноз (т.е. шире доверительный интервал), тем скорее он сбудется. Заметим, что ширина доверительного интервала зависит от размера выборки и дисперсии наблюдений. Вычисление доверительных интервалов основывается на предположении, что переменная в совокупности нормально распределена. Эта оценка может быть неверной, если это предположение не выполнено, и пока размер выборки мал, например, n меньше 100.

 

Медиана

Медиана (термин был впервые введен Гальтоном, 1882) выборки - это значение, которое разбивает выборку на две равные части (при ранжировании). Половина наблюдений лежит ниже медианы, и половина наблюдений лежит выше медианы. Если число наблюдений в выборке нечетно, то медиана вычисляется как среднее двух средних значений. См. также Описательные статистики - Вводный обзор, Описательные статистики - Стартовая панель.

Ранг

Ранг - это последовательное число, определяющее специальное наблюдение в выборке, отсортированной по значениям наблюдений, и поэтому отражающее порядковую связь данного наблюдения с другими в выборке. В зависимости от порядка сортировки (восходящий или нисходящий), высшие ранги представляют высшие значения [то есть восходящие ранги, нижнее значение определяется рангом 1, и высшее значение определяется последним (высшим) рангом] или высшие ранги представляют нижние значения (то есть нисходящие ранги, высшее значение определяется рангом 1). См. Порядковая шкала, Coombs, 1950; см. также Совпадающие ранги.

Технические замечания - Обычные описательные статистики

Выберите опцию Обычные описательные статистики (медиана, мода...) во вкладке Быстрый стартовой панели модуля Непараметрическая статистика для отображения диалогового окна Описательные статистики. Этот диалог позволяет вычислить разнообразные описательные статистики (медиану, процентили, квартили, размах, квартильный размах) и другие описательные статистики (среднее, гармоническое среднее, геометрическое среднее, стандартное отклонение, асимметрию, эксцесс, дисперсию, среднее отклонение и сумму).

Пользователь может также задать определенные процентили, чтобы они были вычислены и отображены в таблице результатов; по умолчанию, программа вычисляет квартили (25%, 75% процентили). Дополнительно стандартные описательные статистики (минимум, максимум, среднее, число наблюдений), а также описанные ниже статистики вычисляются для каждой переменной.

Медиана. Медиана разбивает выборку на две равные части. Пятьдесят процентов наблюдений лежит ниже медианы, пятьдесят процентов - выше медианы. Если значение медианы существенно отличается от среднего, то форма распределения скошена.

Мода. Мода - это максимально часто встречающееся значение в выборке. Частота встречаемости также отображается. Если имеется несколько значений с максимальной частотой, то соответствующий столбец имеет отметку множественная (т.е. имеется несколько мод и распределение, возможно, мультимодально).

Геометрическое среднее. Геометрическое среднее - это произведение всех значений переменной, возведенное в степень 1/n (единица, деленная на число наблюдений). Геометрическое среднее полезно, например, когда шкала измерений нелинейная. Так, в психометрии хорошо известно, что воспринимаемая интенсивность стимулов (например, воспринимаемая яркость света) часто представляет собой логарифмическую функцию реальной интенсивности стимулов (яркости, измеренной в объективных единицах - люксах). В данном примере обычная оценка среднего (сумма значений, деленная на число стимулов), очевидно, не дает верного представления о среднем значении действительной интенсивности стимула, и следует вычислить геометрическое среднее. STATISTICA вычисляет геометрическое среднее с помощью логарифмического преобразования (log):

log(геометрическое среднее) = [S_iⁿ₌₁(log(x_i))]/n

где: x_i - значение наблюдения с номером i; n - число наблюдений.

Если переменная содержит отрицательные значения или нуль (0), геометрическое среднее нельзя вычислить.

Гармоническое среднее. Гармоническое среднее иногда используют для усреднения частот. Гармоническое среднее вычисляется как:

HM = n / S _i=ⁿ₁ (1/x_i)

где: HM - гармоническое среднее, n - число наблюдений, и x_i - значение наблюдения с номером i.

Если в значениях переменной имеется нуль (0), то гармоническое среднее нельзя вычислить.

Дисперсия и стандартное отклонение. Выборочная дисперсия и стандартное отклонение - наиболее часто используемые меры изменчивости или разброса значений переменной (см. Основные статистики и таблицы). STATISTICA вычисляет дисперсию как сумму квадратов отклонений значений переменной от выборочного среднего, деленную на n-1 (но не на n). Стандартное отклонение вычисляется как корень квадратный из оценки дисперсии.

Среднее отклонение. Среднее отклонение представляет собой другую меру изменчивости. Оно вычисляется как сумма абсолютных отклонений значений переменной от выборочного среднего, деленная на n (число наблюдений).

Размах. Размах переменной также является показателем изменчивости. Он вычисляется как наибольшее значение переменной минус наименьшее значение.

Квартильный размах. Квартильный размах равен: верхняя квартиль минус нижняя квартиль (75% процентиль минус 25% процентиль). Так как 75% процентиль (верхняя квартиль) - это значение, слева от которого находятся 75% наблюдений, а 25% процентиль (нижняя квартиль) - это значение, слева от которого находится 25% наблюдений, то квартильный размах - это интервал вокруг медианы, который содержит 50% наблюдений (значений переменной).

Асимметрия. Асимметрия - характеристика несимметричности распределения, а именно – степени скошенности. Распределение скошено влево, если асимметрия отрицательна. Распределение скошено вправо, если асимметрия положительна. Асимметрия стандартного нормального распределения равна 0. Асимметрия связана с третьим моментом и определяется как:

асимметрия = n*M₃/[(n-1)*(n-2)*s³]

где: M₃ равно: S(xi-Среднееx)³, n - число наблюдений, и s³ стандартное отклонение (сигма), возведенное в третью степень.

Эксцесс. Эксцесс - характеристика формы распределения, а именно мера остроты его пика (относительно нормального распределения, эксцесс которого равен 0). Как правило, распределения с более острым пиком, чем у нормального, имеют положительный эксцесс; распределения, пик которых менее острый, чем пик нормального распределения, имеют отрицательный эксцесс. Эксцесс связан с четвертым моментом и определяется формулой:

эксцесс = [n*(n+1)*M₄ - 3*M₂*M₂*(n-1)] / [(n-1)*(n-2)*(n-3)*s⁴]

где: Mj равно: S(xi-Среднееx)^j, n- число наблюдений, и s⁴ стандартное отклонение (сигма) в четвертой степени.

См. Описательные статистики - вкладка Быстрый.

См. также Описательные статистики - Вводный обзор.

Описательные статистики вычисляются отдельно для каждой переменной в файле данных и обеспечивают исследователя такой основной описательной информацией, относительно распределения переменной, как среднее, минимальное и максимальное значение, различные меры изменчивости или вариабельности дисперсий, а также характеристики формы распределения (асимметрия, эксцесс). Эти и другие статистики рассмотрены далее (см. также диалоговое окно Описательные статистики, где приведен полный список доступных статистик). Для вычисления описательных статистик нужно выбрать переменные в текущем файле данных (можно выбрать все переменные одним щелчком кнопки). Далее STATISTICA построит таблицу описательных статистик, расположив их в отдельной строке для каждой переменной. Меры изменчивости (вариабельности) включают стандартное отклонение, и стандартную ошибку. Кроме того, доступны различные критерии нормальности (см. описание диалогового окна Описательные статистики, где дано полное описание имеющихся процедур).

Смотрите другие обзорные статьи по описательным статистикам

"Истинное" среднее и доверительный интервал

Нормальное распределение

Нормальное распределение (этот термин был впервые использован Гальтоном в 1889 г.), также иногда называемое гауссовским, определяется следующим образом:

f(x) = 1/[(2p)^1/2 * s] * e**{-1/2*[(x-m)²/s]²}

-Ґ < x < Ґ

где

m	среднее
s	стандартное отклонение
e	число Эйлера (2.71...)
p	число Пи (3.14...)

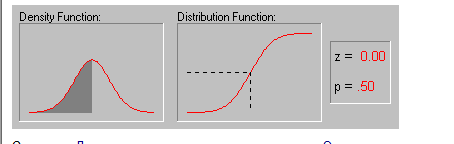См. также Двумерное нормальное распределение, Элементарные понятия (нормальное распределение), Основные статистики - Критерии нормальности, Подгонка распределений - Нормальное распределение, Графики К-К - Нормальное распределение и Графики В-В - Нормальное распределение.

Полный список всех функций распределения см. в разделе Функции распределения, их интегралы и обратные функции распределения.

Дальнейшие сведения об этих статистиках можно найти в разделе Примеры руководства, а также в учебниках по статистике.

Рекомендуемая литература:

Kachigan (1986), Runyon and Haber (1976); для более углубленного понимания элементарной теории основных статистик,

Hays (1988) и особенно фундаментальный курс Kendall and Stuart (1979) (см. перевод: М.Кендалл и А.Стьюарт Теория распределений (том 1), Статистические выводы и связи (том 2), Многомерный статистический анализ (том 3)). На русском языке см., например, книги:

Ивченко Г.И., Медведев Ю.И. Математическая статистика, Высшая школа, 1992.

Боровиков В.П. Популярное введение в программу STATISTICA, Компьютер Пресс 1998. Книга, посвященная анализу данных, построению зависимостей, классификации и прогнозированию в системе STATISTICA.

Боровиков В.П., Боровиков И.П. STATISTICA. Статистический анализ и обработка данных в среде Windows, Филинъ 1998. Справочное и учебное пособие по системе STATISTICA.

Боровиков В.П. STATISTICA, искусство анализа данных на компьютере, Питер 2001. В книге изложена концепция и технология современного анализа данных на компьютере.

Боровиков В.П, Ивченко Г.И. Прогнозирование в системе STATISTICA в среде Windows, Финансы и статистика 1999.

Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика, Наука 1985..

Ю.Неймана Вводный курс теории вероятностей и математической статистики, Наука, 1968 (перевод с английского).

Для врачей полезна книга Наглядная медицинская статистика.