РГР Сопромат. Задача 1. Проведена через основание сечения
 Скачать 19.82 Kb. Скачать 19.82 Kb.
|
|
Вычерчиваем заданную фигуру в масштабе. Вводим в сечении начальную систему координат и изображаем вспомогательные оси 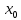 и и 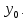 Ось Ось 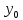 совпадает с осью симметрии сечения, ось совпадает с осью симметрии сечения, ось 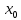 проведена через основание сечения. проведена через основание сечения.Разбиваем сложное сечение на простые фигуры. Для каждого элемента вычисляем необходимые геометрические характеристики. 1 – треугольник Ордината центра тяжести: 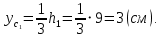 Площадь сечения: 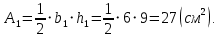 Момент инерции: 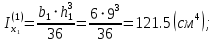 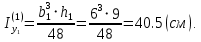 2 – сектор прямоугольник Площадь сечения: 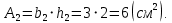 Момент инерции: 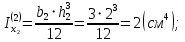 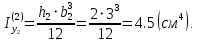 3 – сектор окружность Площадь сечения: 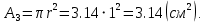 Момент инерции: 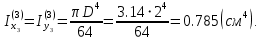 Указываем на чертеже все центры фигур и проводим их центральные оси. Записываем координаты центров фигур в общей системе координат. 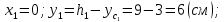 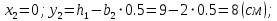 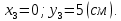 Определяем положение центра тяжести сечения. 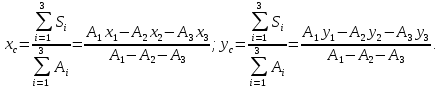 Считаем общую площадь: 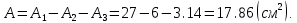 Поскольку ось симметрии 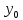 является главной центральной осью является главной центральной осью 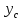 заданного сечения, то абсцисса заданного сечения, то абсцисса 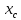 его центра тяжести равна нулю. его центра тяжести равна нулю.Ордината центра тяжести сечения: 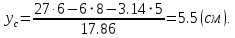 Обозначаем на чертеже общий центр тяжести сечения и проводим центральные оси инерции. Оси 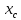 и и 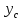 являются главными центральными осями инерции сечения. являются главными центральными осями инерции сечения.Вычисляем главные центральные моменты инерции. 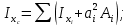 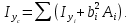 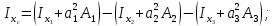 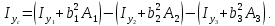 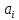 и и 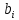 – расстояние между центральными осями – расстояние между центральными осями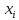 и и 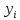 фигуры до лавных центральных осей фигуры до лавных центральных осей 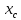 и и 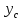 . .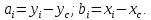 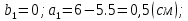 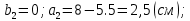 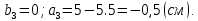 Подставив значения, получим: 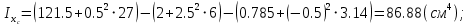 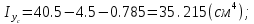 Находим главные центральные радиусы инерции: 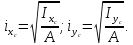 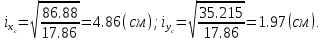 |
