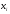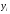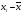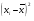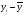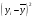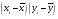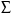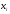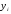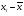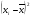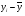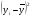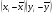корреляция. Проведение корреляционного анализа в планировании и обработке результатов эксперимента
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
 Санкт-Петербургский университет государственной противопожарной службы МЧС России Санкт-Петербургский университет государственной противопожарной службы МЧС РоссииКафедра высшей математики и системного моделирования сложных процессов РЕФЕРАТ по дисциплине: «Планирование и обработка результатов эксперимента» на тему: «Проведение корреляционного анализа в планировании и обработке результатов эксперимента» Выполнил: слушатель магистратуры 1 курса лейтенант вн.службы М.В Рыжих Проверил: профессор кафедры ВМиСМСП к.п.н., доцент Е.С.Калинина Санкт-Петербург 2018 СОДЕРЖАНИЕ Введение 3 1. Понятие корреляционной связи 4 2. Общая классификация корреляционных связей 5 3. Коэффициент корреляции и его свойства 7 4. Значимость коэффициента корреляции 9 5. Виды связи между переменными 10 6. Примеры нахождения коэффициента корреляции 12 Заключение 15 Список литературы 16 Введение Дисциплина планирование и обработка результатов эксперимента является математико-статистической дисциплиной, изучающей методы организации экспериментальных исследований. Именно труды английского ученого-статиста Р. Фишера в 1935 году положили начало планированию эксперимента. Фишер подчеркивал, что именинно результаты планирования эксперимента дают существенный выигрыш в точности оценок. В 60-х годах ХХ века современная теория планирования эксперимента начала складываться как отдельная дисциплина, методы которой были тесно связаны с математических программированием и с теорией приближения функций. Планирование эксперимента заключается в выборе оптимального плана эксперимента, который бы удовлетворял всем заданным требованиям. Важная особенность дисциплины планирование и обработки результатов эксперимента заключается в применении таких методов, которые при расчетах давали бы минимальную погрешность математической модели без потери информации с наименьшими затратами и по которым можно было бы судить об адекватности модели. Цель планирования эксперимента – нахождение таких условий и правил проведения опытов, при которых удастся получить надежную и достоверную информацию об объекте, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности. Среди основных методов планирования, применяемых на разных этапах исследования, одним из самых важных является корреляционный анализ, цель которого заключается в определение зависимости между варьируемыми факторами. 1. Понятие корреляционной связи Нередко при обработке данных исследователи интересуются, как связаны переменные в одной или нескольких изучаемых выборках. Может ли температура воздуха влиять на качество производственного оборудования? Рост влиять на вес человека? и т.д. Такая зависимость между варьируемыми факторами называется корреляционной. Корреляционная связь - это связь между двумя или несколькими переменными, позволяющая судить о том, как с ростом одной переменной изменяется другая. На примере роста и веса человека выявлена положительная корреляционная связь, при увеличении роста- увеличивается и вес человека, но имеются и исключения. Причиной таких исключений является воздействие многих факторов на человека, а именно генетических, психологических, экологических и т .д. Важно помнить, что корреляционная связь не рассматривается как причинно-следственная зависимость, так как она свидетельствует только лишь о наличии связи между переменными. Подводя итог, можно сказать, что задачами корреляционного анализа являются:
2. Классификация корреляционных связей Корреляционные связи можно классифицировать по следующим критериям: по форме, направлению и степени (силе). По форме: прямолинейная или криволинейной. Прямолинейной может быть, например, связь между количеством решенных задач в семестре и получением положительной оценки на зачете (рис.1). То есть, чем больше задач решит студент, тем больше знаний он получит и тем больше вероятность получить положительную оценку на зачете. Криволинейной: например, связь между уровнем мотивации и эффективностью выполнения задачи (рис 2). При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации (максимальная эффективность), дальнейшему повышению мотивации сопутствует уже снижение эффективности.
По направлению корреляционная связь:
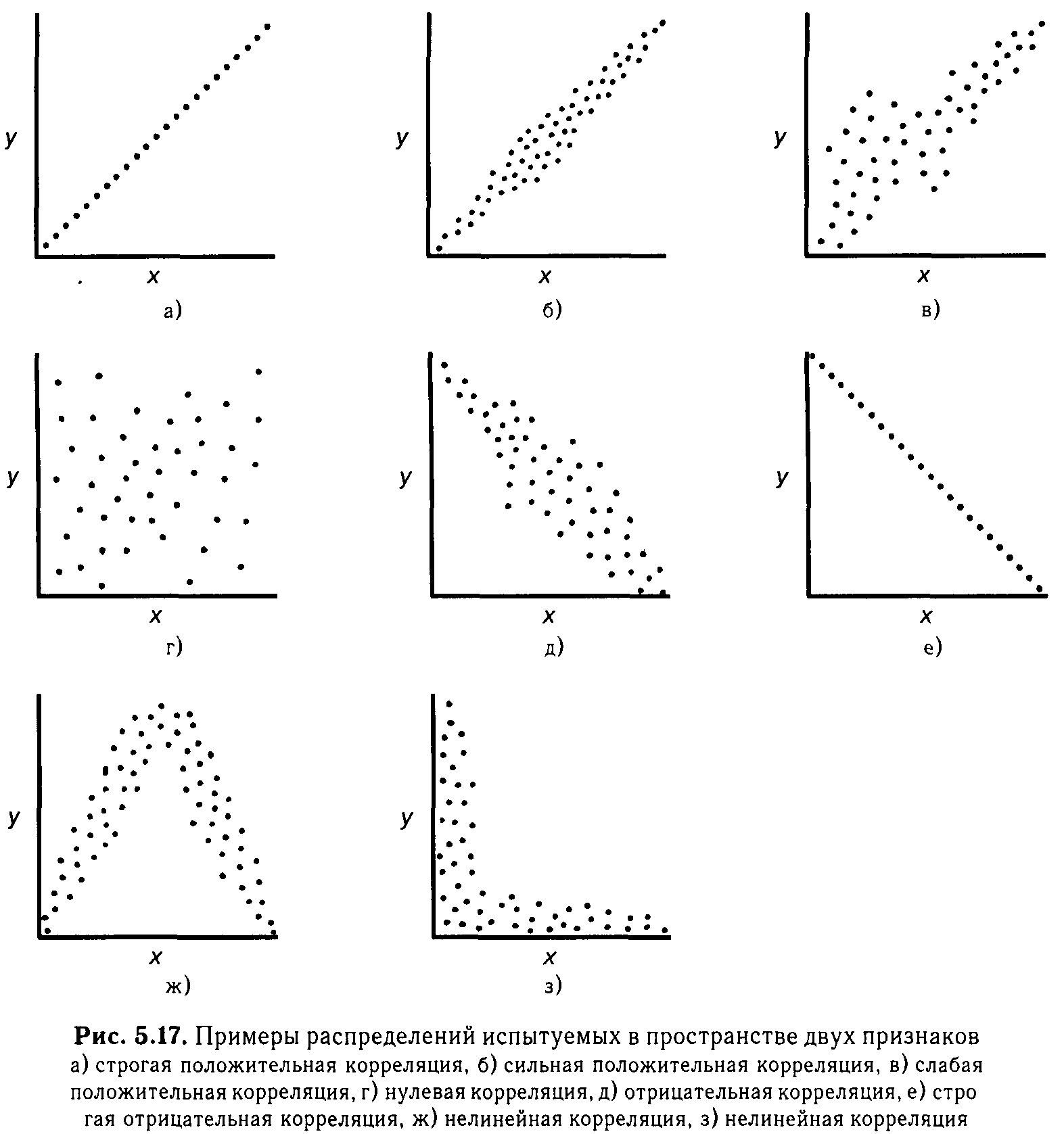  Рис. 3 – Прямая корреляция Рис. 4 – Обратная корреляция  Рис. 5 – Связи нет. Также связь может быть множественной и парной. Простая связь означает наличие двух переменных: 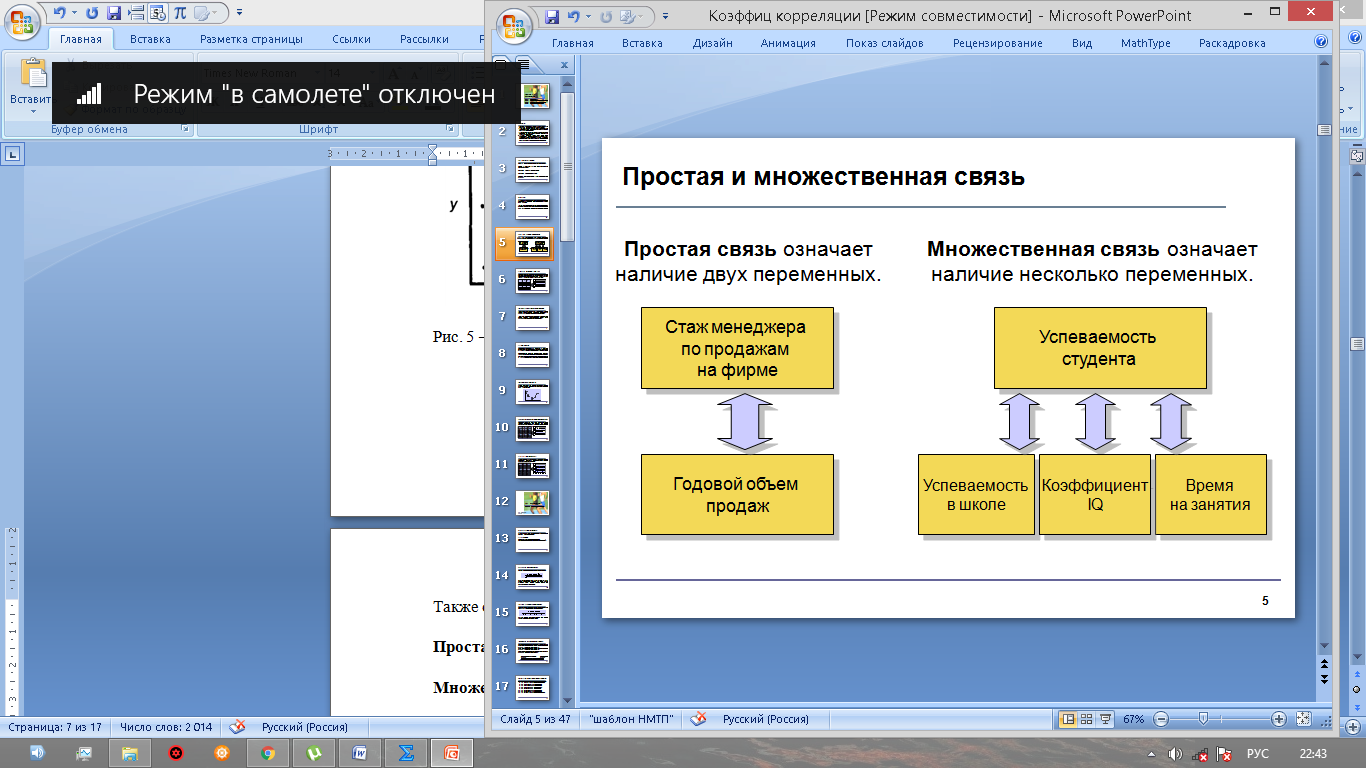 Рис. 6- Простая связь Множественная связь означает наличие несколько переменных: Рис. 7– Множественная связь  3. Коэффициент корреляции и его свойства Как говорилось ранее в п. 1.2., коэффициент корреляции используется для определения тесноты связи между изучаемыми переменными. Коэффициент корреляции является общепринятой в математической статистике характеристикой связи между двумя случайными величинами. Коэффициент корреляции измеряет силу и направление связи между двумя переменными. Обозначения: Выборочный коэффициент корреляции: r Коэффициент корреляции генеральной совокупности: ρ Коэффициент корреляции вычисляется по формуле: 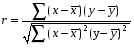 (1) (1)Это, так называемый, коэффициент корреляции Пирсона, равный произведению моментов. Он назван по имени статистика Карла Пирсона, который первый провел исследования в этой области. После несложных преобразований, из первой формулы можно получить другую формулу для коэффициента. 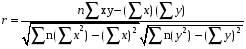 (2) (2)Как мы увидим, она более пригодна для вычисления коэффициента при помощи таблиц. Из формулы видно, что для вычисления r необходимо найти средние значения признаков  и и 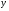 , а также отклонения каждого статистического данного от его среднего , а также отклонения каждого статистического данного от его среднего 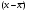 , , 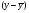 . Зная эти значения, находятся суммы . Зная эти значения, находятся суммы 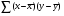 , , 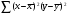 . .Для ясности и полноты знаний о коэффициенте корреляции рассмотрим его основные свойства:
Теснота связи между величинами определяется по величине коэффициента корреляции. Сила связи определяется по шкале Чеддока ( табл.1) Табл. 1- Шкала Чеддока
4. Значимость коэффициента корреляции Коэффициент корреляции генеральной совокупности ρ – это корреляция, вычисленная с использованием всевозможных пар значений признаков (х,у) генеральной совокупности. Требуется: Оценить коэффициент корреляции генеральной совокупности ρ на основе значения коэффициента корреляции выборки r. Условия: Выборочный коэффициент корреляции r используется для оценки ρ, если выполнены следующие предположения:
Чтобы принять верное решение, необходимо воспользоваться процедурой проверки гипотезы. Она включает традиционные пять шагов: Шаг 1. Сформулировать гипотезы. Шаг 2. Построить критическую область. Шаг 3. Вычислить значение критерия. Шаг 4. Сравнить, принять решение. Шаг 5. Написать ответ. Гипотезы формируются следующим образом: Основная гипотеза Н0: ρ = 0 Альтернативная гипотеза Н1: ρ ≠ 0 Основная гипотеза утверждает, что не существует корреляции между признаками х и у в генеральной совокупности. Альтернативная гипотеза утверждает, что корреляция между признаками х и у в генеральной совокупности значима. Когда основная гипотеза отвергается на определенном уровне значимости, это значит, что существует значимое различие между значением r и 0. Когда основная гипотеза принимается, это значит, что значение r не сильно отличается от 0 и является случайным. Для проверки гипотезы используется t-критерий с df = n – 2 степенями свободы: 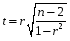 (3) (3)Затем он и сравнивается с табличным значением критерия: если значение 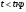 , то нулевая гипотеза принимается, если , то нулевая гипотеза принимается, если 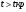 , то Н0 отвергается и принимается альтернативная гипотеза. , то Н0 отвергается и принимается альтернативная гипотеза.5. Виды связи между переменными Когда проверка гипотезы показывает, что существует значимая линейная связь между переменными, исследователь должен рассмотреть возможные виды связи между переменными и выбрать ту, которая диктуется логикой исследования. 1. Прямая причинно-следственная связь 2. Обратная причинно-следственная связь 3. Связь вызвана третьей (скрытой) переменной 4. Взаимосвязь вызвана несколькими скрытыми переменными 5. Связи нет, наблюдаемая зависимость случайна Рассмотрим их на простых примерах, описанных ниже 1. Прямая причинно-следственная связь между переменными(переменная х определяет значение переменной у). Наличие воды ускоряет рост растений. Яд вызывает смерть. Температура воздуха прямо влияет на скорость таяния льда. 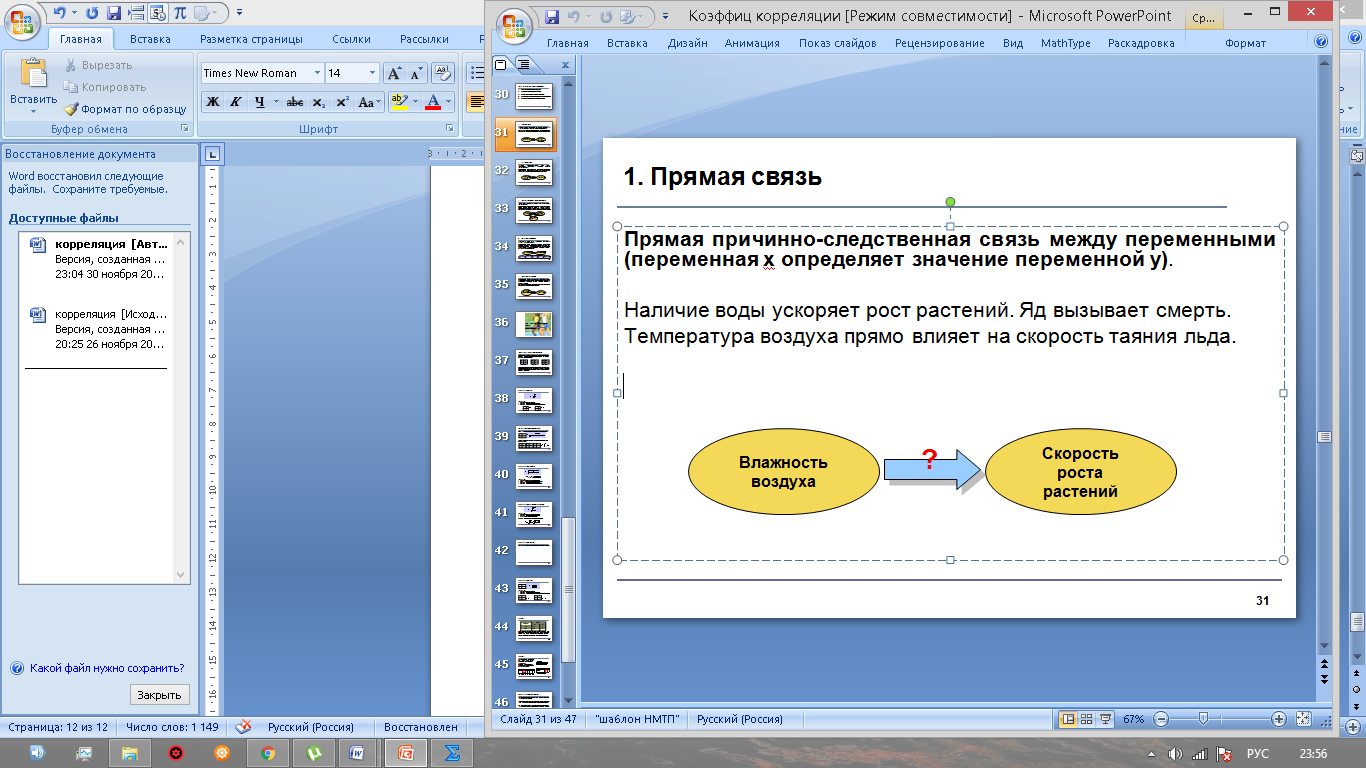 Рис. 8 - Прямая причинно-следственная связь 2. Обратная причинно-следственная связь между переменными(переменная у определяет значение переменной х). Исследователь может думать, что чрезмерное потребление кофе вызывает нервозность. Но, может быть, очень нервный человек выпивает кофе, чтобы успокоить свои нервы? 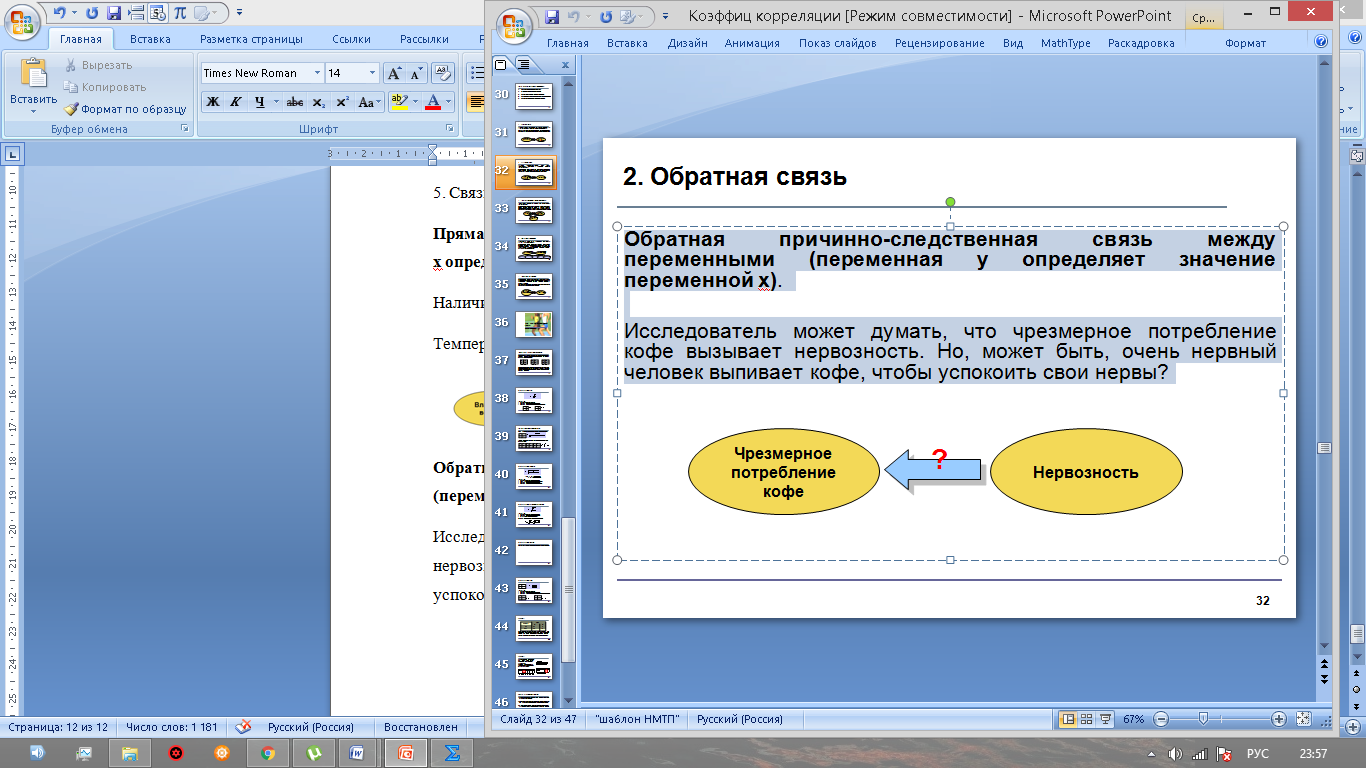 Рис. 9 - Обратная причинно-следственная связь 3.Связь между переменными может быть вызвана третьей переменной. Исследователь установил, что существует некая зависимость между числом утонувших людей и числом выпитых безалкогольных напитков в летнее время. А может быть, обе переменные связаны с жарой и потребностью людей во влаге? 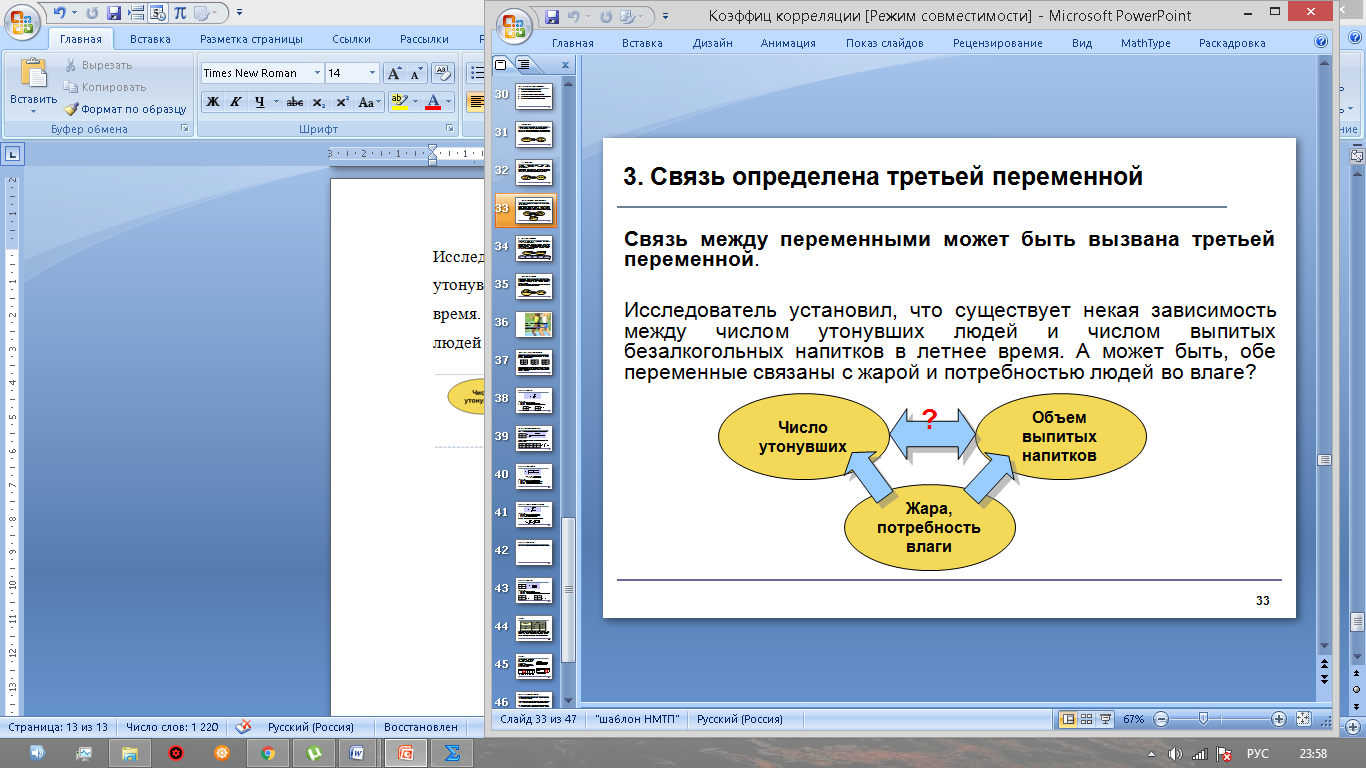 Рис. 10 - Связь, вызванная третьей переменной 4.Несколько переменных Взаимосвязь может быть определена несколькими скрытыми переменными. Исследователь может обнаружить значимую связь между оценками студентов в университете и оценками в школе. Но, возможно, действуют и другие переменные: IQ, количество часов занятий, влияние родителей, мотивация, возраст, авторитет преподавателей. 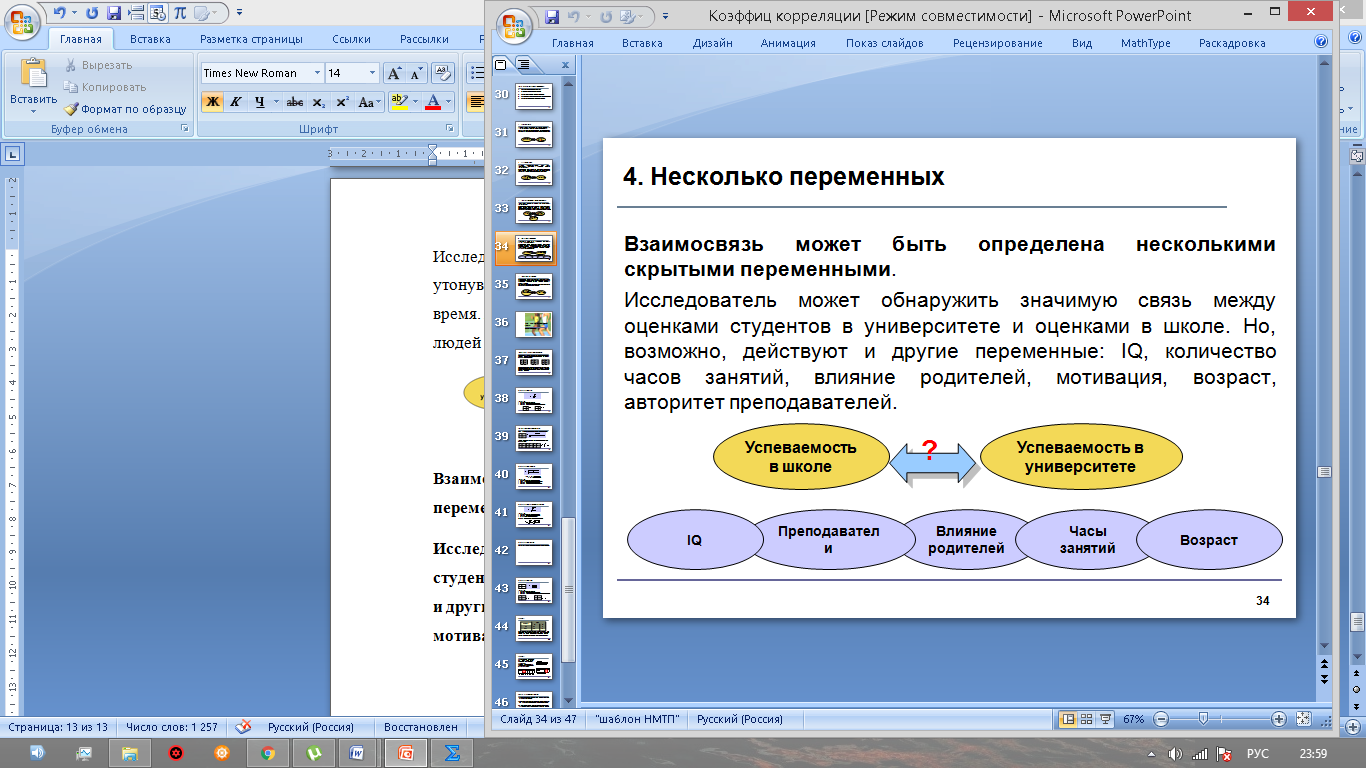 Рис.11- Связь нескольких переменных 5.Зависимость случайна Исследователь может найти значимую зависимость между увеличением количества людей, которые занимаются спортом и увеличением количества людей, которые совершают преступления. Но здравый смысл говорит, что любая связь между этими двумя переменными должна быть случайной.  Рис.12 -Зависимость случайна 6.Примеры нахождения коэффициента корреляции Для успешного усвоения данного материала рассмотрим примеры нахождения коэффициента корреляции. Пример №1: Установите, есть ли взаимосвязь между оперативными данными МЧС и Рослесхоза за август по количеству природных пожаров. Табл. 2- Исходные данные
Решение. Определим выборочный коэффициент корреляции по формуле (1), промежуточные результаты вычислений представим в таблице 3. Табл. 3-Промежуточные результаты
Найдем среднее число пожаров для каждого из признаков: 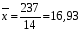 , , 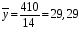 . . Выборочный коэффициент корреляции равен 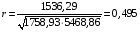 . Так как выборочный коэффициент корреляции равен 0,495, то между признаками связь слабая. . Так как выборочный коэффициент корреляции равен 0,495, то между признаками связь слабая.Пример №2: Десять испытуемых в эксперименте по запоминанию в ситуации с помехами и без них имели следующие результаты (в балах): Табл. 4- Исходные данные
Существует ли значимая корреляционная связь между показателями? Решение. Определим выборочный коэффициент корреляции по формуле (1), промежуточные результаты представим в таблице 5. Табл. 5-Промежуточные результаты
Средние значения равны 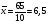 , , 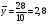 . Выборочный коэффициент корреляции равен . Выборочный коэффициент корреляции равен 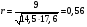 . Так как . Так как 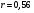 , то между признаками существует хорошая связь. , то между признаками существует хорошая связь.Заключение Список используемой литературы |