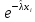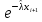Расчетно-графическая работа по теме «Проверка гипотезы о законе распределения случайной величины», Вариант 23. Расчетно-графическая работа, в23. Проверка гипотезы о законе распределения случайной величины
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Расчетно-графическая работа по теме «Проверка гипотезы о законе распределения случайной величины» Вариант №23 Количество точек – 60, число интервалов – 10; 0.29 0.57 2.60 1.48 0.11 0.48 1.53 0.06 0.15 0.90 0.00 0.42 0.55 0.90 3.43 0.17 0.64 1.48 2.60 0.12 0.78 0.08 0.60 0.66 0.24 0.31 2.35 1.32 0.26 0.32 0.95 2.35 0.60 3.15 1.53 0.15 0.87 1.18 2.47 1.18 0.27 4.50 1.92 0.95 0.85 0.18 0.80 1.32 0.17 0.14 0.06 0.55 1.99 0.76 0.33 0.97 1.05 0.33 0.38 0.18 1. Исходные выборочные данные, расположенные в порядке возрастания: 0.00 0.06 0.06 0.08 0.11 0.12 0.14 0.15 0.15 0.17 0.17 0.18 0.18 0.24 0.26 0.27 0.29 0.31 0.32 0.33 0.33 0.38 0.42 0.48 0.55 0.55 0.57 0.60 0.60 0.64 0.66 0.76 0.78 0.80 0.85 0.87 0.90 0.90 0.95 0.95 0.97 1.05 1.18 1.18 1.32 1.32 1.48 1.48 1.53 1.53 1.92 1.99 2.35 2.35 2.47 2.60 2.60 3.15 3.43 4.50 Объем выборки n=60; xmax=4.50, xmin=0.00, размах выборки: xmax-xmin=4.50-0.00=4.50 2. Разбиваем отрезок [xmin,xmax] на k=10 интервалов равной длины h=4.50/10=0.45. Эти интервалы: [0.00; 0.45], (0.45; 0.90], (0.90; 1.35], (1.35; 1.80], (1.80; 2.25], (2.25; 2.70], (2.70; 3.15], (3.15; 3.60], (3.60; 4.05], (4.05; 4.50]. Точки деления: х1=0.00, х2=0.45, х3=0.90, х4=1.35, х5=1.80, х6=2.25, х7=2.70, х8=3.15, х9=3.60, х10=4.05, х11=4.50. 3. Для всех i=1,…,10 находим следующие числа:ni – частоты интервалов; ni/(nh) ; xi*- середины интервалов;xi*‧ni ; (xi*)2‧ni. Таблица 1.
4. Строим гистограмму и приводим график плотности вероятности теоретического соответствующего распределения. 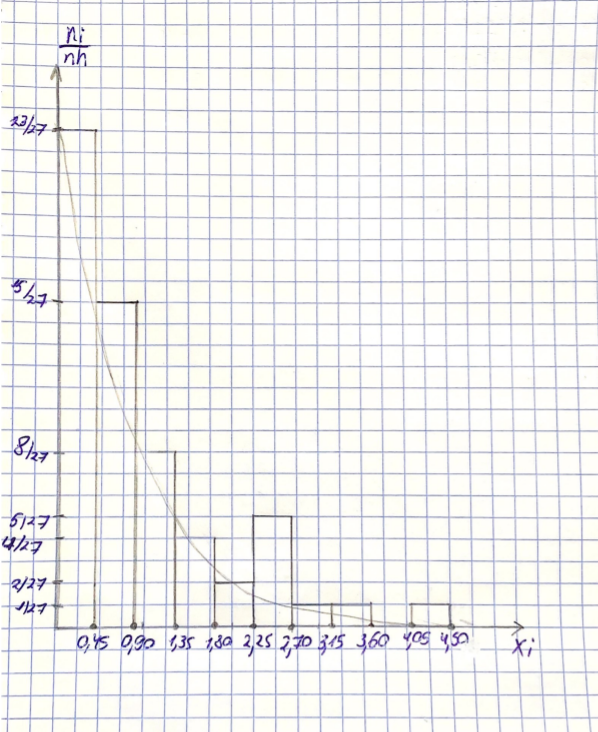 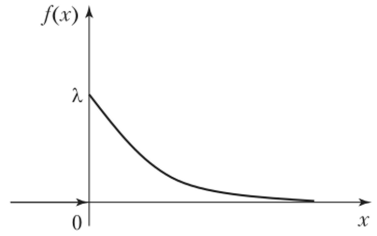 Рис.3а Рис. 3б Гипотеза: изучаемая случайная величина имеет показательное распределение; соответствующая плотность вероятности имеет следующий вид: 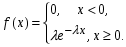 где 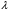 >0 – любое число. >0 – любое число.5. Оцениваем параметры распределения: Параметр λ можно оценить двумя способами: 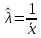 и и 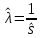 , ,где 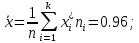 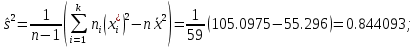 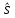 =0.918745. =0.918745.Тогда 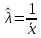 =1.0417 и =1.0417 и 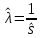 =1.08844. =1.08844.Возьмем в качестве итогового значения 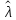 среднее арифметическое этих чисел: среднее арифметическое этих чисел: 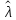 =1.06507. =1.06507. 6. Для всех i=1,…,10 находим числа числа pi по формуле: 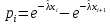 . .Далее находим числаnpi, ni-npi, (ni-npi)2/ npiи вносим их в таблицу 2. Таблица 6.
7. Находим статистику Пирсона: 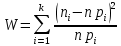 . W=7.326862. . W=7.326862.Число степеней свободы статистики W равно m=k-1-q =10-1-1=8. 8. Задаем уровень значимости α=0.05 и по таблице квантилей для χ2 - распределения находим χ2α.m = χ20.05, 8 = 15.5. Критерий согласия Пирсона: если W< χ2α.m . то гипотезу о законе распределения случайной величины принимаем с надежностью 95%; в противном случае гипотезу отвергаем. Так как W=7.326862< χ20.05, 8 =….... то гипотезу о показательном распределении с параметром λ =1.06507 принимаем (с надежностью 95%). |