вариант1692. 1. Исходные данные варианта заданий
 Скачать 1.7 Mb.
|
|
Задание 1 Имеются следующие выборочные данные за год по предприятиям одной из отраслей экономики региона (выборка 10%-ная механическая): Таблица 1.1. Исходные данные варианта заданий
По исходным данным: 1) постройте статистический интервальный ряд распределения предприятий по признаку «Основные фонды», образовав пять групп с равными интервалами; 2) рассчитайте значения моды и медианы полученного интервального ряда распределения; 3) рассчитайте следующие статистические характеристики ряда распределения: среднюю арифметическую, дисперсию, среднее квадратическое отклонение, коэффициент вариации, представив расчеты в табличном виде. Сделайте выводы по результатам выполнения пунктов 1 - 3. 1. Построение интервального ряда распределения Расчет величины h и границ интервалов ряда: 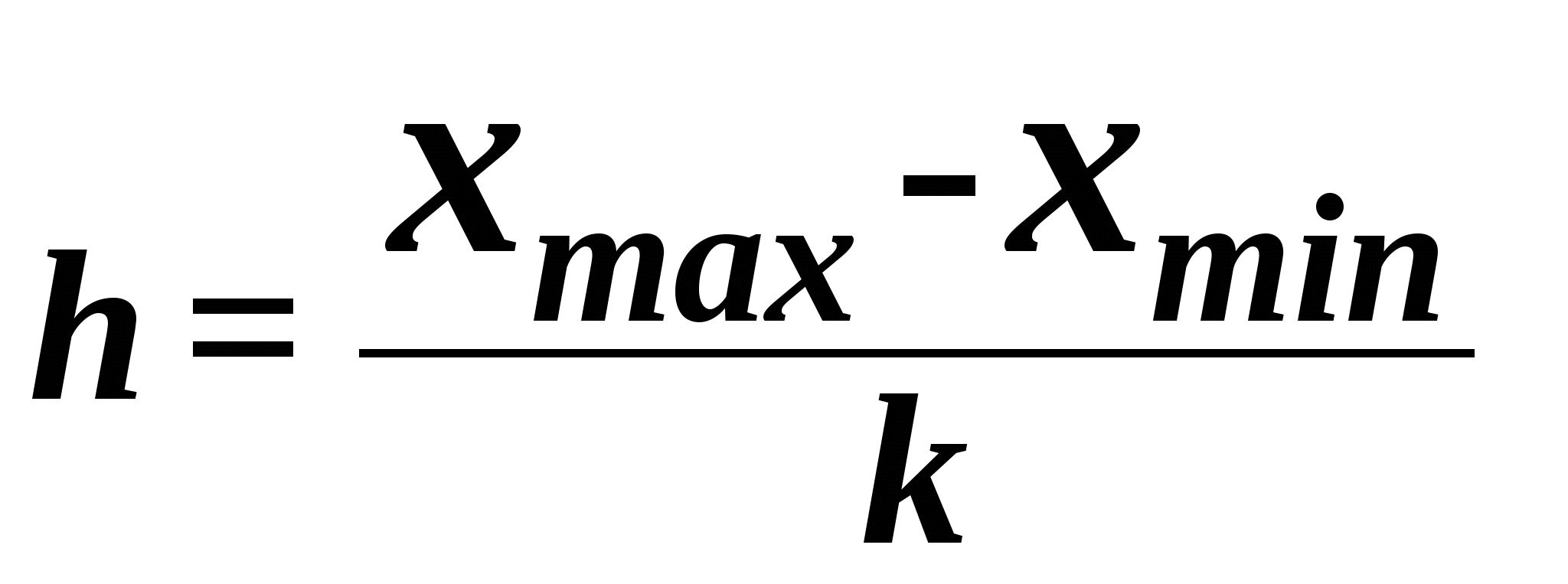 =  млн. руб. (  – наибольшее и наименьшее значения признака в исследуемой совокупности, k- число групп интервального ряда).Границы интервалов ряда распределения приведены в табл.1.2. Таблица 1.2 Границы интервалов ряда распределения
Интервальный ряд распределения предприятий по величине основных фондов представлен в виде табл. 1.3.
Вывод. Анализ интервального ряда распределения изучаемой совокупности предприятий показывает, что распределение предприятий по размеру основных фондов является равномерным. 2. Расчет значений моды и медианы ряда распределения Формула расчета моды:  где хМo – нижняя граница модального интервала, h –величина модального интервала, fMo – частота модального интервала, fMo-1 – частота интервала, предшествующего модальному, fMo+1 – частота интервала, следующего за модальным. Модальным является интервал с наибольшей частотой, т.е. в нашем случае распределение многомодальное. Формула расчета медианы : 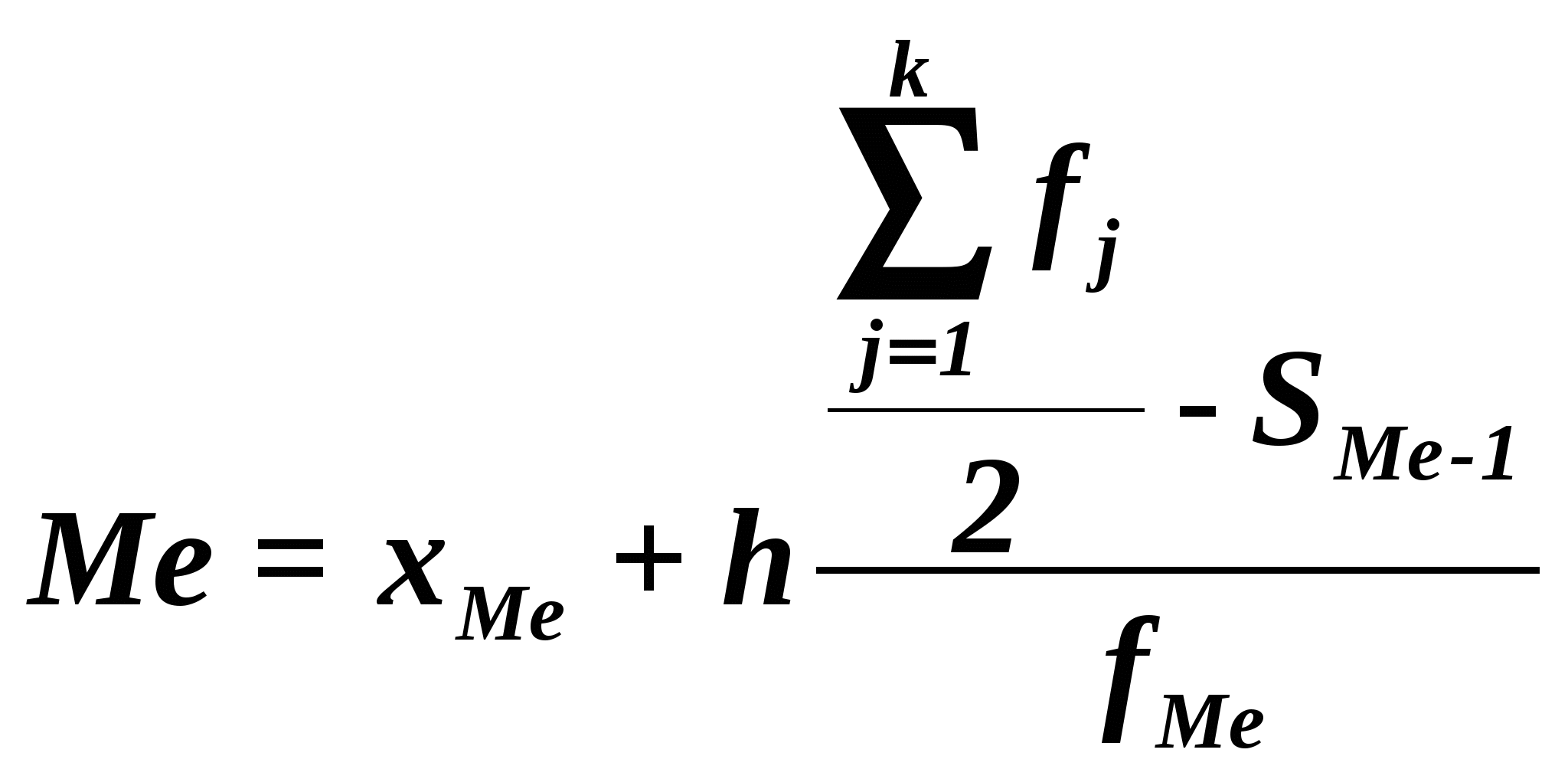 ,где хМе– нижняя граница медианного интервала, h – величина медианного интервала,  – сумма всех частот,fМе – частота медианного интервала, SMе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному. Медианным является интервал 269,2 – 409,6, впервые превышает величину, равную половине численности единиц совокупности (  = )Расчет значения медианы :  Вывод. В рассматриваемой совокупности предприятий половина предприятий имеют в среднем размер основных фондов не более 620,2 млн. руб., а другая половина – не менее 620,2 млн. руб. 3. Расчет характеристик ряда распределения Для расчета характеристик ряда распределения  , σ, σ2, Vσ на основе табл. 1.3 строится вспомогательная табл. 1.4 (  – середина j-го интервала).Таблица 1. 4 Расчетная таблица для нахождения характеристик ряда распределения
Расчет средней арифметической взвешенной:  млн.руб.Расчет дисперсии: 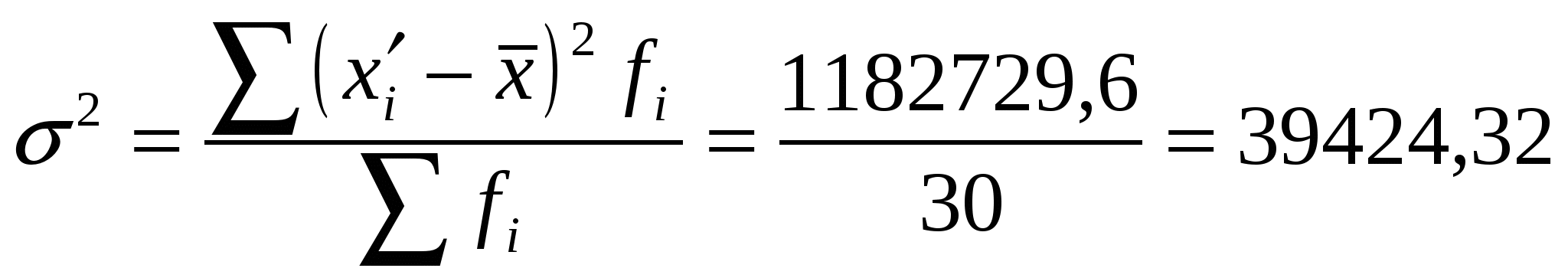 39424,32Расчет среднего квадратического отклонения: млн. руб. Расчет коэффициента вариации:  . Вывод. Анализ полученных значений показателей и σ говорит о том, что средний размер основных фондов составляет 620,2 млн. руб.; отклонение от среднего размера в ту или иную сторону составляет в среднем 198,56 млн. руб. (или 32,02%); наиболее характерные значения размера основных фондовнаходятся в пределах от 421,64 млн. руб. до 818,76млн. руб. (диапазон  ).Значение Vσ =32,02 не превышает 33%, следовательно, вариация размера основных фондов в исследуемой совокупности предприятий незначительная и совокупность по данному признаку качественно однородна. Расхождение между значениями и Ме отсутствует (= 620,2 млн. руб., Ме= 620,2 млн. руб.), что подтверждает вывод об однородности совокупности предприятий. Таким образом, найденное среднее значение размера основных фондов (620,2 млн. руб.) является типичной, надежной характеристикой исследуемой совокупности предприятий.Задание 2 По исходным данным (табл.1.1) с использованием результатов выполнения задания 1: 1) методом аналитической группировки установите наличие и направление корреляционной связи между факторным признаком Х - «Основные фонды» и результативным признаком Y - «Прибыль от продажи продукции»; 2) по исходным данным постройте линейную однофакторную регрессионную модель зависимости признака Y от фактора Х ; 3) проверьте найденную модель на адекватность; 4) рассчитайте средний коэффициент эластичности взаимосвязи признаков. Сделайте выводы по результатам выполнения задания. На основе первичных данных (табл. 1.1) взаимосвязь между изучаемыми признаками графически отображается в виде поля корреляции (рис. 2.1). На основе первичных данных (табл. 1.1) взаимосвязь между изучаемыми признаками графически отображается в виде поля корреляции (рис. 2.1). 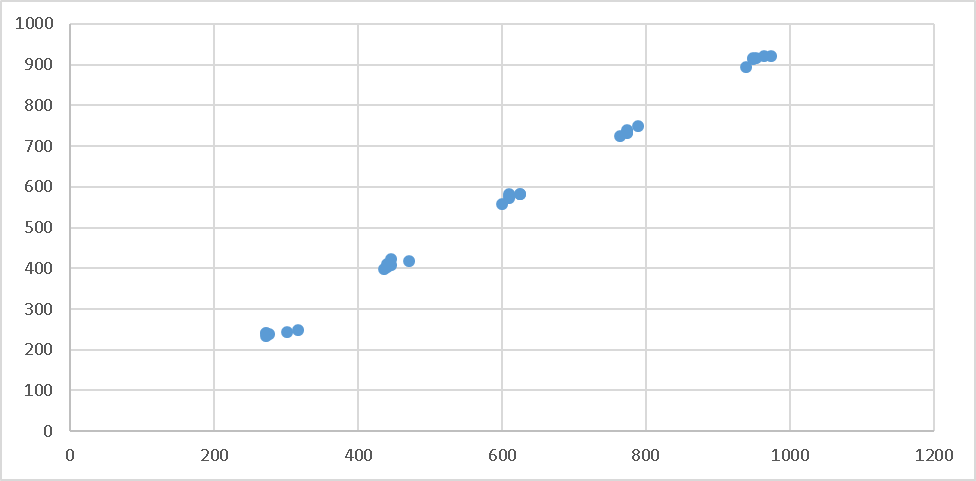 Рис.2.1. Поле корреляции взаимосвязи изучаемых признаков Как видно из рисунка 2.1 наблюдается не беспорядочное рассеивание точек по полю, а достаточно четкая их концентрация (корреляционное облако). Так как точки распределяются от нижнего левого угла поля в сторону верхнего правого, можно предположить, что между признаками есть связь и она прямая. Для того, чтобы определить, является ли связь корреляционной, применяется метод аналитической группировки по фактору Х (используется ряд распределения табл.1.3). Аналитическая таблица для анализа корреляционной связи между факторным признаком Х - «Основные фонды» и результативным признаком Y - «Прибыль от продажи продукции» имеет вид. Таблица 2.1 Зависимость суммы прибыли от размера основных фондов
Вывод. Анализ данных табл. 2.1 показывает, что с увеличением размера выручки Х от группы к группе систематически возрастают и групповые средние прибыли Y, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками. 2. Построение линейной однофакторной регрессионной модели зависимости результативного признака Y от фактора Х. На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер. Линейное уравнение регрессии имеет вид y = bx + a Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, a и b соответственно оценки параметров α и β регрессионной модели, которые следует найти. Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Система нормальных уравнений. a*n + b*∑x = ∑y a*∑x + b*∑x2 = ∑y*x Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
Для наших данных система уравнений имеет вид 30a + 18373*b = 17415 18373*a + 12924370,2*b = 12339309,4 Получаем эмпирические коэффициенты регрессии: b = 1.001, a = -32.5378 Уравнение регрессии (эмпирическое уравнение регрессии): y = 1.001 x -32.5378 Параметры уравнения регрессии. Выборочные средние. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||