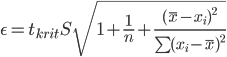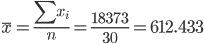
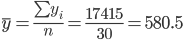
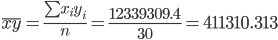
Выборочные дисперсии:
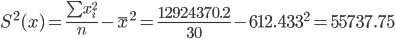
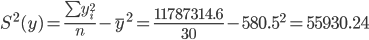
Среднеквадратическое отклонение
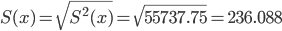
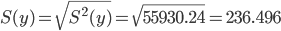
Коэффициент корреляции.
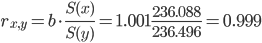
Ошибка аппроксимации.
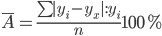
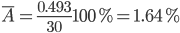
В среднем, расчетные значения отклоняются от фактических на 1.64%. Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
R2= 0.9992 = 0.9985
т.е. в 99.85% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 0.15% изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации).
Для оценки качества параметров регрессии построим расчетную таблицу (табл. 2)
x
|
y
|
y(x)
|
(yi-ycp)2
|
(y-y(x))2
|
|y - yx|:y
|
971
|
926
|
939,421
|
119370,25
|
180,111
|
0,0145
|
761,8
|
730,8
|
730,014
|
22590,09
|
0,618
|
0,00108
|
607,6
|
577,6
|
575,662
|
8,41
|
3,756
|
0,00336
|
314,2
|
252,2
|
281,972
|
107780,89
|
886,391
|
0,118
|
433,4
|
403,4
|
401,29
|
31364,41
|
4,452
|
0,00523
|
946
|
921
|
914,396
|
115940,25
|
43,614
|
0,00717
|
607,6
|
587,6
|
575,662
|
50,41
|
142,518
|
0,0203
|
771,8
|
744,8
|
740,024
|
26994,49
|
22,811
|
0,00641
|
468,4
|
423,4
|
436,325
|
24680,41
|
167,043
|
0,0305
|
299,2
|
249,2
|
266,958
|
109759,69
|
315,329
|
0,0713
|
961
|
927
|
929,411
|
120062,25
|
5,811
|
0,0026
|
771,8
|
736,8
|
740,024
|
24429,69
|
10,394
|
0,00438
|
622,6
|
587,6
|
590,677
|
50,41
|
9,466
|
0,00524
|
438,4
|
408,4
|
406,295
|
29618,41
|
4,431
|
0,00515
|
274,2
|
244,2
|
241,933
|
113097,69
|
5,14
|
0,00928
|
946
|
919
|
914,396
|
114582,25
|
21,198
|
0,00501
|
771,8
|
739,8
|
740,024
|
25376,49
|
0,0502
|
0,000303
|
622,6
|
587,6
|
590,677
|
50,41
|
9,466
|
0,00524
|
443,4
|
428,4
|
411,3
|
23134,41
|
292,416
|
0,0399
|
269,2
|
245,2
|
236,928
|
112426,09
|
68,427
|
0,0337
|
951
|
921
|
919,401
|
115940,25
|
2,557
|
0,00174
|
786,8
|
754,8
|
755,039
|
30380,49
|
0,057
|
0,000316
|
438,4
|
415,4
|
406,295
|
27258,01
|
82,903
|
0,0219
|
607,6
|
582,6
|
575,662
|
4,41
|
48,137
|
0,0119
|
269,2
|
247,2
|
236,928
|
111088,89
|
105,516
|
0,0416
|
936
|
900
|
904,386
|
102080,25
|
19,237
|
0,00487
|
771,8
|
738,8
|
740,024
|
25058,89
|
1,498
|
0,00166
|
597,6
|
562,6
|
565,652
|
320,41
|
9,315
|
0,00542
|
443,4
|
413,4
|
411,3
|
27922,41
|
4,411
|
0,00508
|
269,2
|
239,2
|
236,928
|
116485,69
|
5,162
|
0,0095
|
18373
|
17415
|
17415
|
1677907,1
|
2472,238
|
0,493
|
Оценка параметров уравнения регрессии.
Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
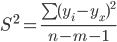
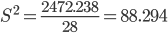
S2 = 88.294 - необъясненная дисперсия или дисперсия ошибки регрессии (мера разброса зависимой переменной вокруг линии регрессии).
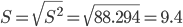
S = 9.4 - стандартная ошибка оценки (стандартная ошибка регрессии).
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bxi ± ε)
где
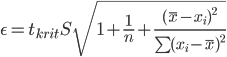
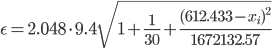
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
xi
|
y = -32,54 + 1xi
|
εi
|
ymin = y - εi
|
ymax = y + εi
|
971
|
939,421
|
20,277
|
919,144
|
959,697
|
761,8
|
730,014
|
19,688
|
710,326
|
749,702
|
607,6
|
575,662
|
19,562
|
556,1
|
595,224
|
314,2
|
281,972
|
20,059
|
261,913
|
302,032
|
433,4
|
401,29
|
19,743
|
381,547
|
421,033
|
946
|
914,396
|
20,182
|
894,214
|
934,578
|
607,6
|
575,662
|
19,562
|
556,1
|
595,224
|
771,8
|
740,024
|
19,705
|
720,319
|
759,729
|
468,4
|
436,325
|
19,679
|
416,645
|
456,004
|
299,2
|
266,958
|
20,11
|
246,848
|
287,067
|
961
|
929,411
|
20,238
|
909,172
|
949,649
|
771,8
|
740,024
|
19,705
|
720,319
|
759,729
|
622,6
|
590,677
|
19,563
|
571,114
|
610,239
|
438,4
|
406,295
|
19,733
|
386,562
|
426,028
|
274,2
|
241,933
|
20,199
|
221,733
|
262,132
|
946
|
914,396
|
20,182
|
894,214
|
934,578
|
771,8
|
740,024
|
19,705
|
720,319
|
759,729
|
622,6
|
590,677
|
19,563
|
571,114
|
610,239
|
443,4
|
411,3
|
19,723
|
391,577
|
431,023
|
269,2
|
236,928
|
20,218
|
216,71
|
257,146
|
951
|
919,401
|
20,201
|
899,2
|
939,601
|
786,8
|
755,039
|
19,733
|
735,305
|
774,772
|
438,4
|
406,295
|
19,733
|
386,562
|
426,028
|
607,6
|
575,662
|
19,562
|
556,1
|
595,224
|
269,2
|
236,928
|
20,218
|
216,71
|
257,146
|
936
|
904,386
|
20,146
|
884,24
|
924,532
|
771,8
|
740,024
|
19,705
|
720,319
|
759,729
|
597,6
|
565,652
|
19,563
|
546,089
|
585,215
|
443,4
|
411,3
|
19,723
|
391,577
|
431,023
|
269,2
|
236,928
|
20,218
|
216,71
|
257,146
|
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
F-статистика. Критерий Фишера.
|
 Скачать 1.7 Mb.
Скачать 1.7 Mb.