Проверочная работа по геометрии (теория) 7 класс 1 полугодие вариант 1 Треугольник является остроугольным, если
 Скачать 127.5 Kb. Скачать 127.5 Kb.
|
|
Проверочная работа по геометрии (теория) 7 класс 1 полугодие ВАРИАНТ 1 1. Треугольник является остроугольным, если: а) среди его углов нет тупого угла б) каждый его угол меньше прямого угла в) среди его углов нет прямого угла г) каждый его угол меньше тупого угла 2. Треугольник в котором один из углов развернутый называется: а) равносторонним б) развернутым в) такого треугольника не существует г) тупоугольным 3. Если стороны одного угла являются дополнительными лучами сторон другого угла, то такие углы называются: а) смежными б) вертикальными в) соответственными г) равными 4. Если углы имеют одну общую сторону, а две другие стороны являются дополнительными лучами, то такие углы называются: а) смежными б) вертикальными в) односторонними г) равными 5. Что можно сказать про смежные углы: а) они равны б) их сумма образует развернутый угол в) каждый из них прямой г) каждый их них является острым углом 6. Прямые называются перпендикулярными, если: а) они лежат на параллельных прямых б) они не пересекаются в) они образуют прямой угол при пересечении г) они образуют два острых угла при пересечении 7. Какие из следующих утверждений верны: а) смежные углы имеют общую вершину б) вертикальные углы имеют общую вершину в) смежные углы равны г) смежные углы могут быть равны 90° 8. Какие из следующих утверждений неверны: а) вертикальные углы равны б) если углы равны, то они вертикальные в) смежные углы равны г) перпендикулярные отрезки имеют общую точку 9. Два треугольника равны, если: а) две стороны одного треугольника равны двум сторонам другого треугольника б) два угла одного треугольника равны двум углам другого треугольника в) две стороны и угол одного треугольника равны двум сторонам и углу другого треугольника г) две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника 10. Если треугольник равнобедренный, то: а) он равносторонний б) любая его медиана является биссектрисой в) углы при основании равны г) боковые стороны равны 11. Если треугольник равносторонний, то: а) он равнобедренный б) все его углы прямые в) любая его высота является медианой, биссектрисой и высотой г) только одна высота является медианой 12. В каком треугольнике только одна его высота делит треугольник на два равных треугольника? а) в любом б) в равнобедренном в) в равностороннем г) в тупоугольном 13. На какие углы делит медиана сторону треугольника: а) на равные б) на смежные в) на прямые г) на острые 14. Установи соответствие:
14. Вставь пропущенные слова: 1) _________________ угла называют луч с началом в ____________ угла, делящий этот угол на два равных угла. 2) Два угла, отличных от ______________, называют _____________, если стороны одного угла являются дополнительными ________ сторон другого угла. 3) Отрезок, соединяющий вершину треугольника с серединой ______________________________, называют ___________ треугольника. 4) Если биссектриса треугольника является ____________, то треугольник равнобедренный. 5) Треугольник, у которого все __________________, называют равносторонним. 6) Если сумма _______________ углов, образующихся при пересечении двух прямых секущей, равна _______, то прямые параллельны. 15. Назови все треугольники, которые являются: а) равнобедренными б) равносторонними в) прямоугольными 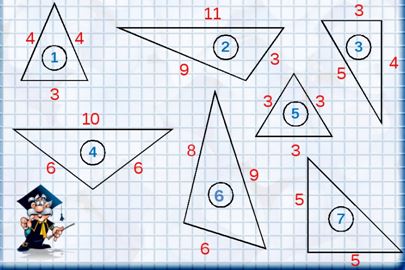 16. Запиши определение высоты треугольника: ___________________________________________________ ______________________________________________________________________________________________________________________________________________________________________________________________ 17. Нарисуй
ВАРИАНТ 2 1. Треугольник является прямоугольным, если: а) среди его углов нет тупого угла б) каждый его угол меньше прямого угла в) среди его углов нет прямого угла г) один из его углов прямой 2. Треугольник является тупоугольным, если: а) каждый его угол меньше прямого угла б) среди его углов нет прямого угла в) каждый из его углов тупой г) один из его углов больше прямого 3. Если стороны одного угла являются дополнительными лучами сторон другого угла, то такие углы называются: а) смежными б) вертикальными в) соответственными г) равными 4. Если углы имеют одну общую сторону, а две другие стороны являются дополнительными лучами, то такие углы называются: а) смежными б) вертикальными в) односторонними г) равными 5. Что можно сказать про вертикальные углы: а) они равны б) их сумма образует развернутый угол в) каждый из них прямой г) каждый их них является острым углом 6. Прямые называются параллельными, если: а) одна прямая является продолжением другой прямой б) они не пересекаются в) они образуют прямой угол при пересечении г) они образуют два острых угла при пересечении 7. Какие из следующих утверждений верны: а) смежные углы имеют общую вершину б) накрест лежащие углы всегда равны в) смежные углы равны г) вертикальные углы равны 8. Какие из следующих утверждений неверны: а) в равнобедренном треугольнике углы равны б) в равностороннем треугольнике все углы равны в) односторонние углы являются смежными г) перпендикулярные лучи имеют общую точку 9. Два треугольника равны, если: а) две стороны одного треугольника равны двум сторонам другого треугольника б) два угла одного треугольника равны двум углам другого треугольника в) сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащих к ней угла другого треугольника, то такие треугольники равны г) стороны и два угла одного треугольника равны стороне и двум углам другого треугольника 10. Если треугольник равнобедренный, то: а) он равносторонний б) два угла при основании равны в) все углы равны г) два угла равны 11. Если треугольник равносторонний, то: а) биссектриса, высота и медиана, проведенные из одной вершины совпадают б) все его углы равны в) все его углы тупые г) только одна высота является медианой 12. В каком треугольнике любая высота делит треугольник на два равных треугольника? а) в любом б) в равнобедренном в) в равностороннем г) в тупоугольном 13. На какие углы делит высота сторону треугольника: а) на равные б) на смежные в) на прямые г) на острые 14. Установи соответствие:
14. Вставь пропущенные слова: 1) Перпендикуляр, опущенный из _____________ треугольника на ____________, содержащую _________________ сторону называется ______________ треугольника. 2) Два угла называются _____________, если у них одна сторона ________, а две другие являются __________________ лучами. 3) Если ________ треугольника является его биссектрисой, то этот треугольник ____________________. 4) В _________________ треугольнике биссектриса, высота и медиана, проведенные из _____ вершины, __________. 5) Если _____________ углы, образующие при пересечении двух прямых ____________, равны, то такие прямые параллельны. 6) Прямую, перпендикулярную отрезку и проходящую через его _______________ называют ______________ перпендикуляром отрезка. 15. Назови все треугольники, которые являются: а) равнобедренными б) равносторонними в) тупоугольными  16. Запиши определение медианы треугольника: __________________________________________________ ______________________________________________________________________________________________________________________________________________________________________________________________ 17. Нарисуй
|
