билеты по информатика мирэа. 13-16 билеты. Прямой код Назначение предназначен для отображения целых и дробных чисел со знаком (можно закодировать вещественное число). Правила перевода чтобы получить прямой код, нужно к указанным разрядам добавить в качестве старшего знаковый разряд
 Скачать 24.13 Kb. Скачать 24.13 Kb.
|
|
Прямой, обратный, дополнительный коды, модифицированные коды: определение, назначение, правила перевода, достоинства и недостатки (на примере двоичной системы). Все коды построены на основе позиционной традиционной системы счисления Прямой код: Назначение: предназначен для отображения целых и дробных чисел со знаком (можно закодировать вещественное число). Правила перевода: чтобы получить прямой код, нужно к указанным разрядам добавить в качестве старшего знаковый разряд. При этом письменно знаковый разряд должен быть отделен точкой для повышения наглядности. Если знаковый разряд равен 0 - число положительное. Если равен N-1 (N - основание системы) - число отрицательное (пример 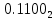 = =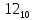 , , 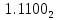 = =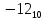 Достоинства: 1. Получить прямой код числа достаточно просто. 2. Коды положительных чисел относительно беззнакового кодирования остаются неизменными. 3. Кол-во положительных чисел равно количеству отрицательных. Недостатки: 1.Выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора (например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого). 2.Существуют два нуля: +0 (100…000) и -0 (000…000), из-за чего усложняется ариф. Сравн) Обратный код: строится на основе прямого кода, является промежуточным этапом при переводе в доп код Определение: обратный код — это математический метод, позволяющий заменить операцию вычитание на операцию сложение, при этом положительные числа в дополнительном коде выглядят так же как и в прямом, а отрицательные меняются Правила перевода: положительные числа в обратном коде выглядят так же, как и в прямом, отрицательные формируются следующим образом: ставится знаковый разряд (1), а затем записывается положительное число с инвертированными цифрами N-битное число в обратном коде содержит N-1 значащих разрядов и 1 знаковый! Дополнительный код: строится на основе обратного кода Определение: Дополнительный код — это математический метод, позволяющий заменить операцию вычитание на операцию сложение (это ещё и назначение дополнительного кода), при этом положительные числа в дополнительном коде выглядят так же как и в прямом, а отрицательные меняются Обратный код N-разрядного отрицательного числа является дополнением этого модулем числа до максимального числа, которое можно записать при помощи N разрядов Правила перевода: доп. Код N-разрядного отрицательного числа образуется как дополнение модуля этого числа до нуля, к которому приписывается знаковый разряд в качестве старшего (знак 0 - число положительное, максимальная цифра - число отрицательное). В знаковый разряд отрицательных чисел ставится единица, далее берется число в обратном коде, и к младшему разряду арифметическим образом прибавляется единица. 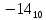 = =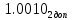 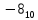 = =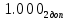 Альтернативный способ перевода. Нужно переписать все биты исходного числа справа налево до первой единицы, включая ее. Остальные биты инвертировать. Поставить знаковый разряд. Преимущества и недостатки те же что и в прямом коде 1.Возможность заменить арифметическую опе-рацию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, Недостатки: 1.Ряд положительных и отрицательных чисел несимметричен. 2.В отличие от сложения, числа в дополнительном коде нельзя сравнивать как беззнаковые, или вычитать без расширения разрядности. Модифицированный код: строится на основе обратного кода Определение: Правила перевода: В модифицированных кодах используются два знаковых разряда: 00 – положительное число 11 – отрицательное число 01 – положительное число с переполнением 10 отрицательное число с переполнением Правила вычислений в модифицированных кодах такие же, как и в дополнительных. Сложение и вычитание в обратном и дополнительном коде. Переполнение и его устранение (на примере двоичной системы). Обратный код
67+78: 0,1000011 В данном случае переполнение является 0,1001110 признаком выхода числа из разрядной 1,0010001 сетки, так что запятую следует перенести на разряд влево. Ответ будет выглядеть 0,10010001 -67+78: 1.0111100 Произошло переполнение, 1 слева 0.1001110 10,0001010 прибавляем к числу. 0,0001010 1 0,0001011 67-78: 0.1000011 1.0110001 Ответ можно перевести в прямой код: 1.1110100 1,0001011= -1110 -67-78: 1.0111100 Произошло переполнение. 1 прибавляем 1.0110001 к числу 10.1101101 1.1101101 Если складываются 2 отр. 1. то при переполнении в 1.1101110 знаковом остается 1 Дополнительный код
67+78: 0.1000011 0.1001110 1.0010001 В данном случае переполнение является признаком выхода числа из разрядной сетки, так что запятую следует перенести на разряд влево. Ответ будет выглядеть 0,10010001 -67+78: 1.0111101 0.1001110 10.0001011 Перенос игнорируется (если разные знаки). 67-78: 0.1000011 1.0110010 1.1110101 Чтобы перевести число в прямой код, нужно отнять 1, потом инвертировать. -67-78 1.0111101 1.0110010 10.1101111 Переполнение является признаком выхода числа из разрядной сетки, так что запятую следует перенести на разряд влево.1.01101111 *если перед запятой получается 11 (например, -8-6) 1.1000 1.1010 11.0010, то первая 1 игнорируется, за исключение случая, когда после запятой все 0, тогда это указывается на переполнение и надо осуществить сдвиг влево (например, -60-68=-128 1.1000100 1.0111100 Код со смещением: определение, назначение, правила выполнения сложения и вычитания. Позволяет сдвинуть числовую шкалу, содержащую как отрицательные, так и положительные числа, полностью в область положительных чисел. Если n – доступное количество разрядов, то 2^(n-1)-максимальное число в смещенном коде, записываемое как 1..1; 1-2^(n-1)-минимальное число в смещенном коде, записываемое как 0..0; 2^(n-1)-1-величина смещения; При выполнении арифметических операций необходимо учитывать смещение. Чтобы получить в конце верный результат, смещение необходимо вычесть. Представление чисел с фиксированной точкой: варианты фиксации точки для чисел со знаком и без, диапазоны представления чисел. Целочисленные типы данных. Варианты фиксации точки: Справа от младшего разряда Где-то в середине сетки Слева от старшего разряда Числа с точкой справа от младшего разряда могут быть Без знака (только положительные) n разрядов в сетке Диапазон: 0..1- 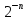 Со знаком 1 разряд занимает знак, остается n-1 Диапазон: 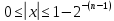 Фиксированная в середине Без знака Диапазон 0.. 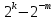 Со знаком Диапазон 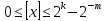 Фиксированная в слева Без знака Диапазон 0.. 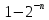 n разрядов n разрядовСо знаком Диапазон 0 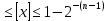 n разрядов n разрядовЦелочисленные типы: Беззнаковые целые Целые со знаком |
