|
|
Лекции_2_05,06 Прямой метод Ляпунова. (1). Прямой метод Ляпунова
Прямой метод Ляпунова.
Так как устойчивость движения по Ляпунову эквивалентна устойчивости нулевого состояния равновесия системы в отклонениях, то ограничиваются, как правило, исследованием системы в отклонениях. Одним из сильнейших методов исследования устойчивости нулевого состояния равновесия является при этом прямой метод Ляпунова. Существо метод состоит в том, что знакоопределенные вещественные функции используются как мера отклонения состояния системы от точки покоя.
Пусть  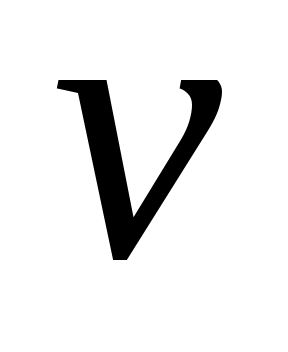 :E :E - непрерывно дифференцируемое в окрестности S начала координат отображение E в - непрерывно дифференцируемое в окрестности S начала координат отображение E в  (точнее, (точнее, 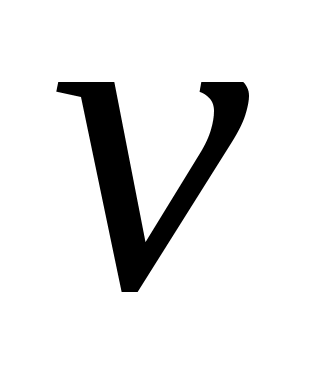 - дифференцируемый по Фреше функционал, заданный в окрестности начала координат пространства состояний). Если - дифференцируемый по Фреше функционал, заданный в окрестности начала координат пространства состояний). Если 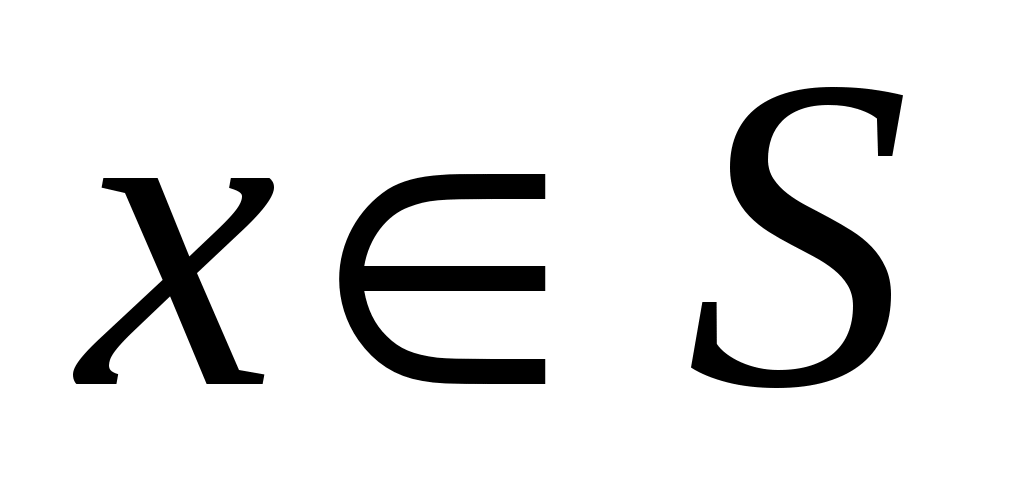 , то обозначим через , то обозначим через 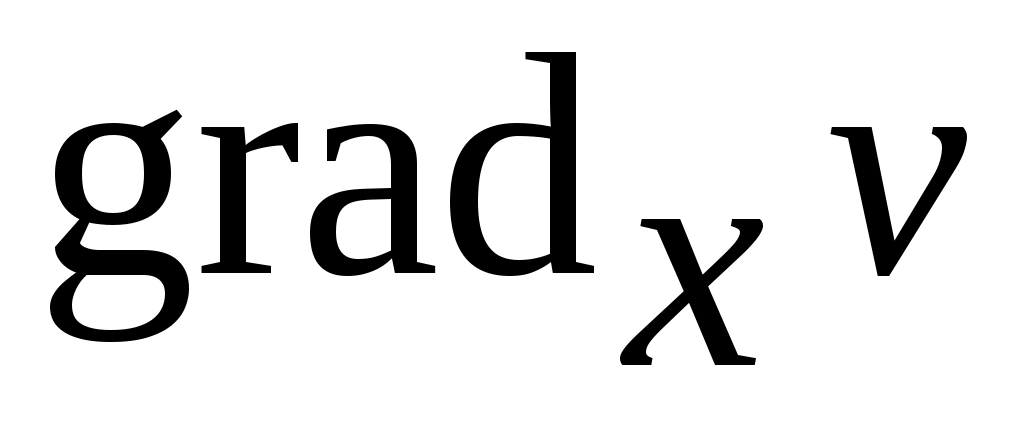 градиент градиент 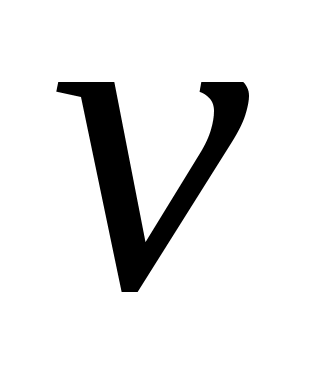 в точке в точке 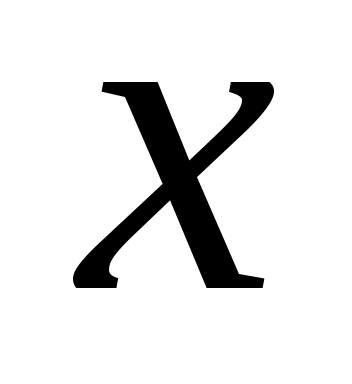 (производную Фреше функционала (производную Фреше функционала 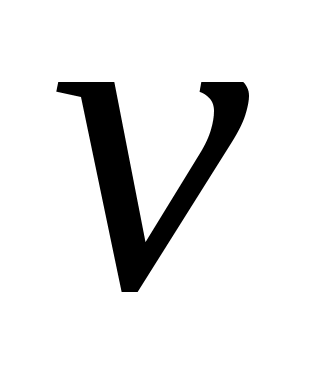 в точке в точке 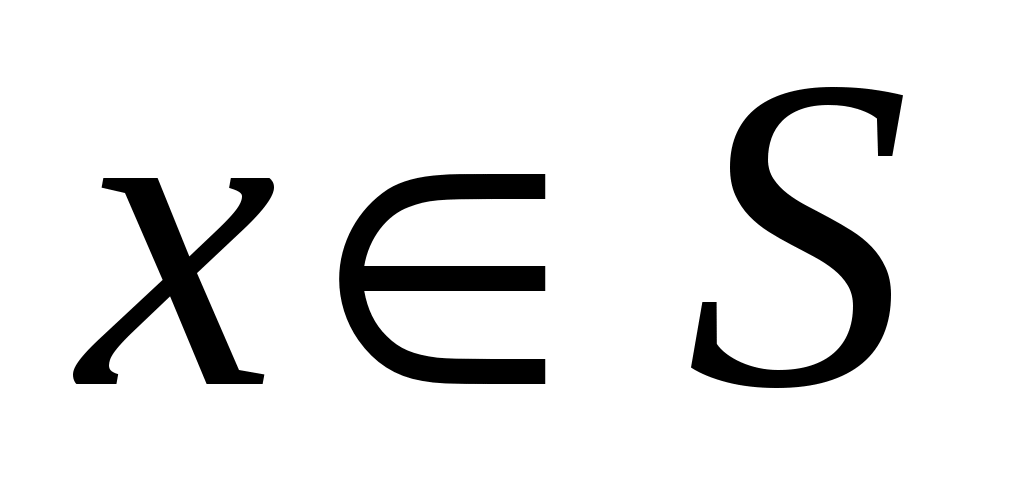 ). Функционал ). Функционал 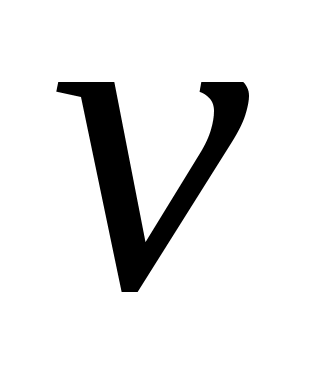 , равный нулю в начале координат, назовем знакопостоянным положительным в окрестности , равный нулю в начале координат, назовем знакопостоянным положительным в окрестности 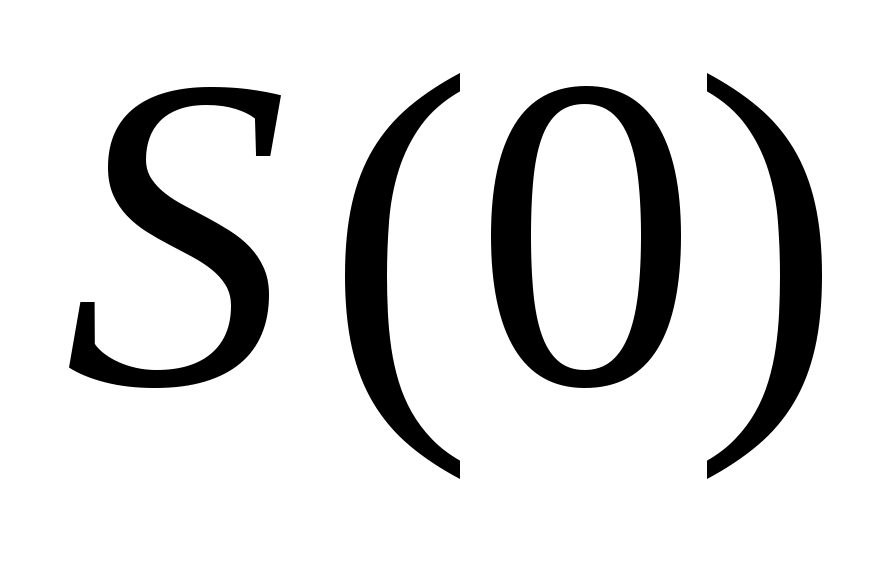 , если , если 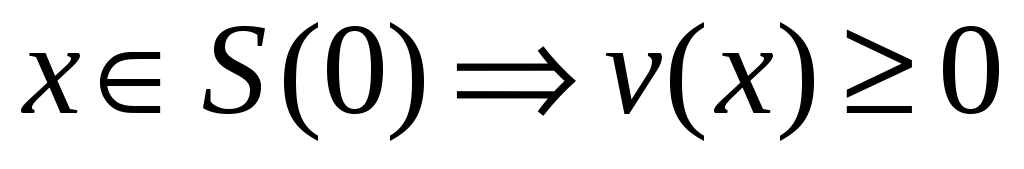 . Знакоположительный функционал . Знакоположительный функционал 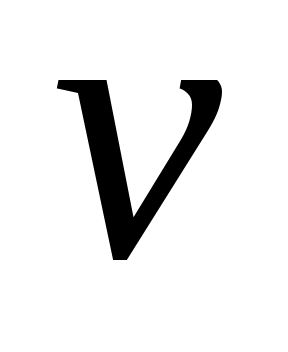 :E :E назовем положительно определенным, если для всех нулевых назовем положительно определенным, если для всех нулевых 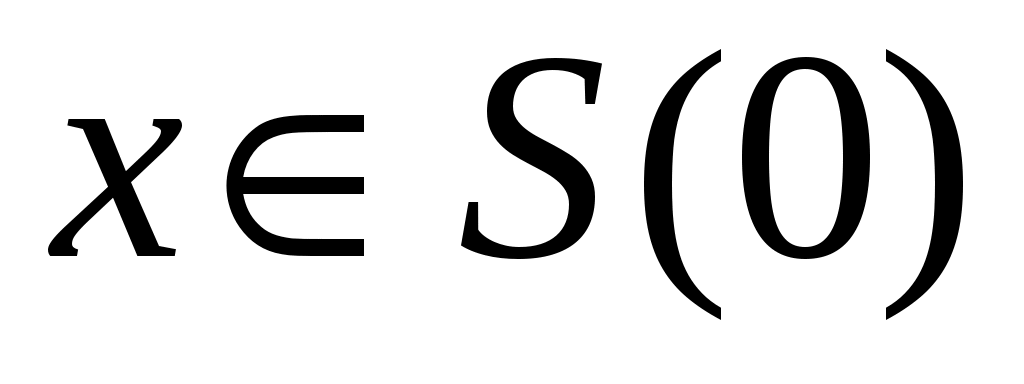 его значение строго положительно. его значение строго положительно.
Аналогично вводится понятие отрицательно определенных в 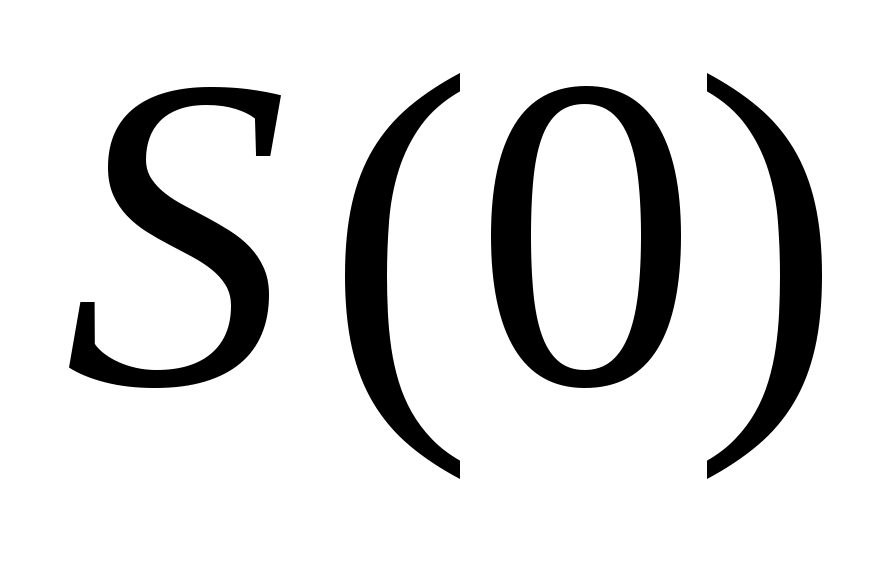 функционалов. В том случае, если рассматривается дифференцируемое отображение функционалов. В том случае, если рассматривается дифференцируемое отображение 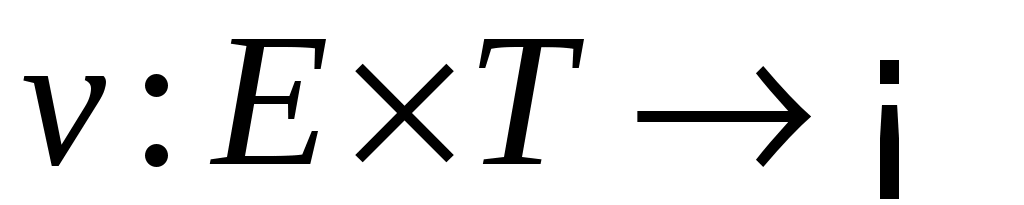 , т.е. если рассматриваются функции , т.е. если рассматриваются функции 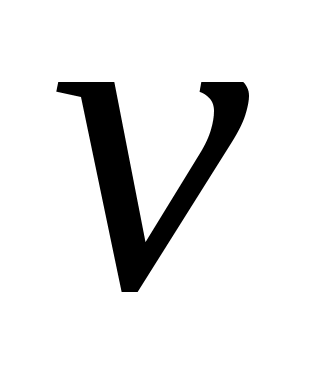 , значения которых , значения которых 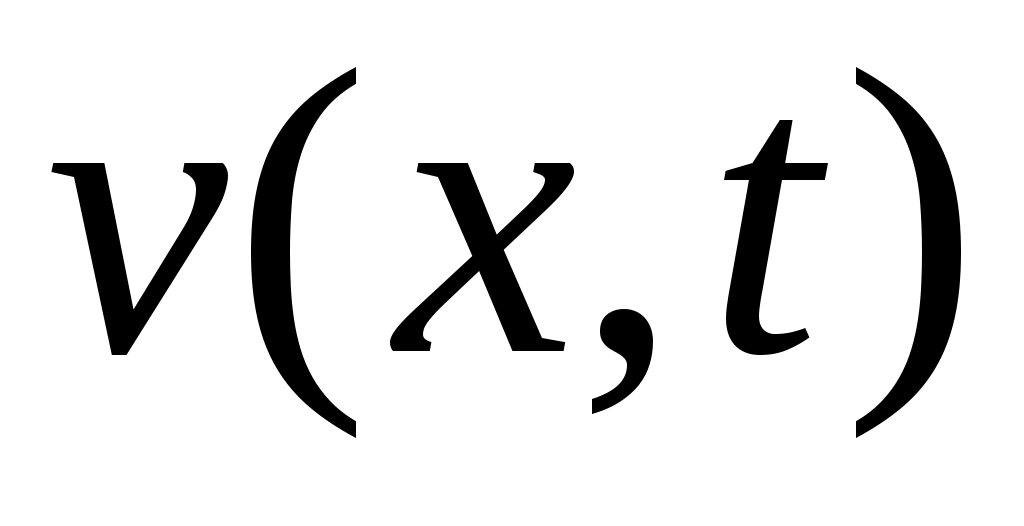 определяются как вектором состояний определяются как вектором состояний 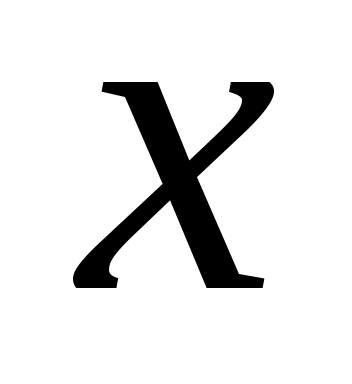 , так и моментом времени , так и моментом времени 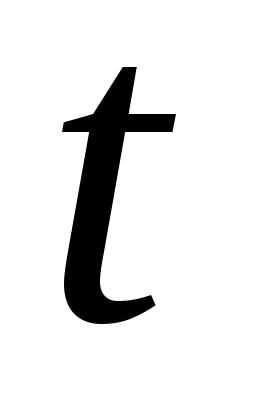 , то функции , то функции 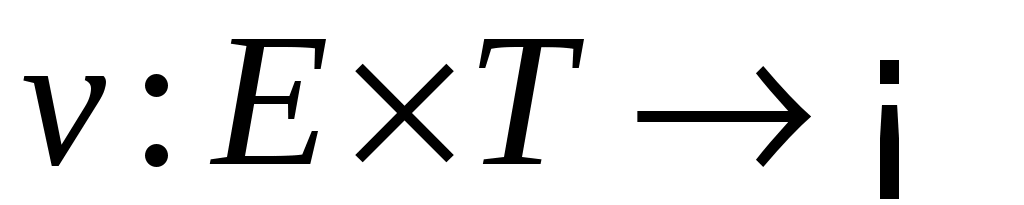 называются знакопостоянными (знакоопределенными) положительными в окрестности называются знакопостоянными (знакоопределенными) положительными в окрестности 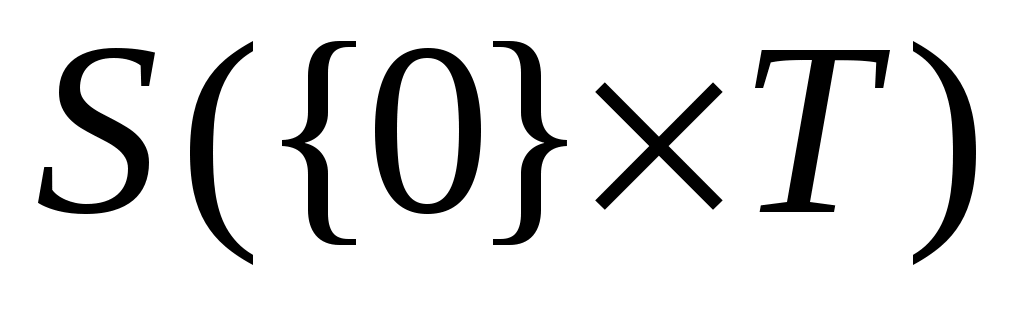 траектории невозмущенного движения системы в отклонениях, если траектории невозмущенного движения системы в отклонениях, если 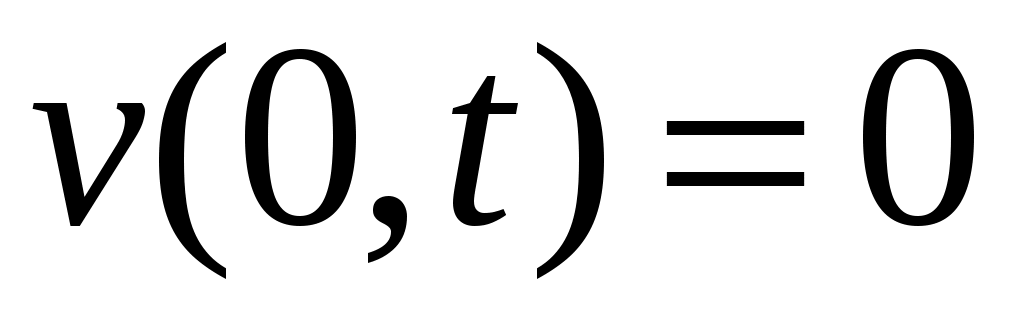 для всех для всех 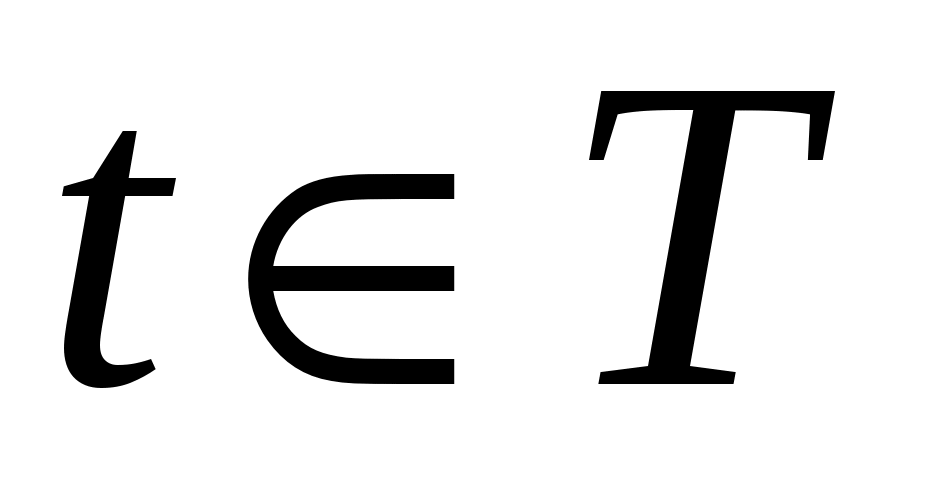 и если найдется такой знакопостоянный (знакоопределенный) положительный функционал, не зависящий от времени и если найдется такой знакопостоянный (знакоопределенный) положительный функционал, не зависящий от времени  , что при любых , что при любых 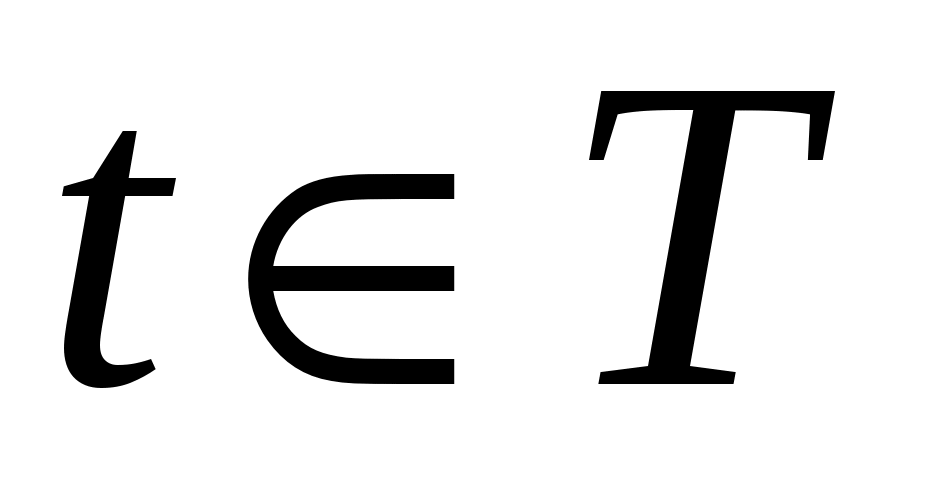 из из 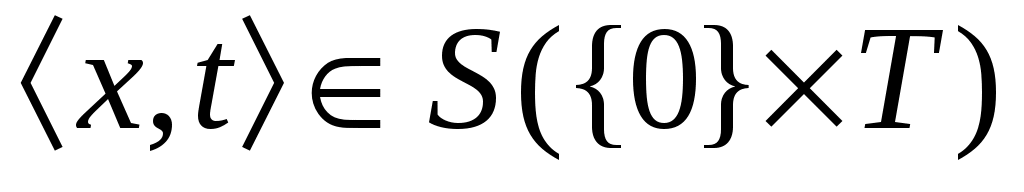 следует, что следует, что 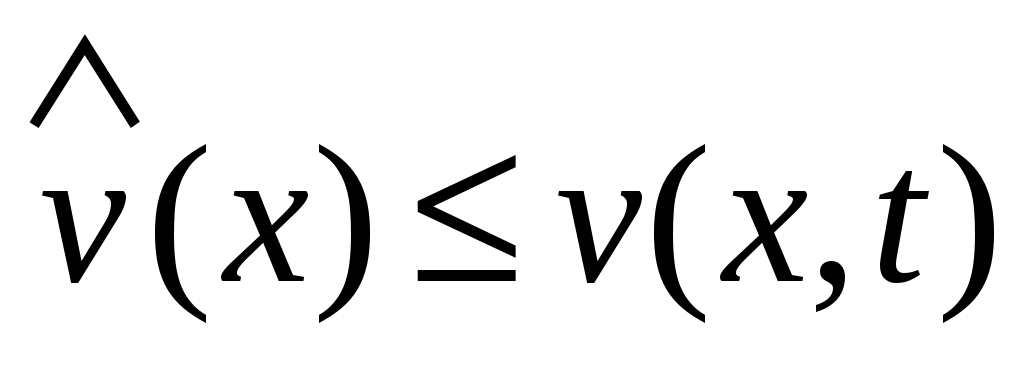 . Аналогично вводится понятие знакопостоянных (знакоопределенных) отрицательных функций. . Аналогично вводится понятие знакопостоянных (знакоопределенных) отрицательных функций.
Изменение значений функций 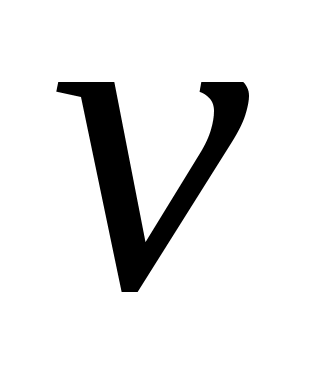 в процессе движения системы может быть определено, если задать начальные условия в процессе движения системы может быть определено, если задать начальные условия 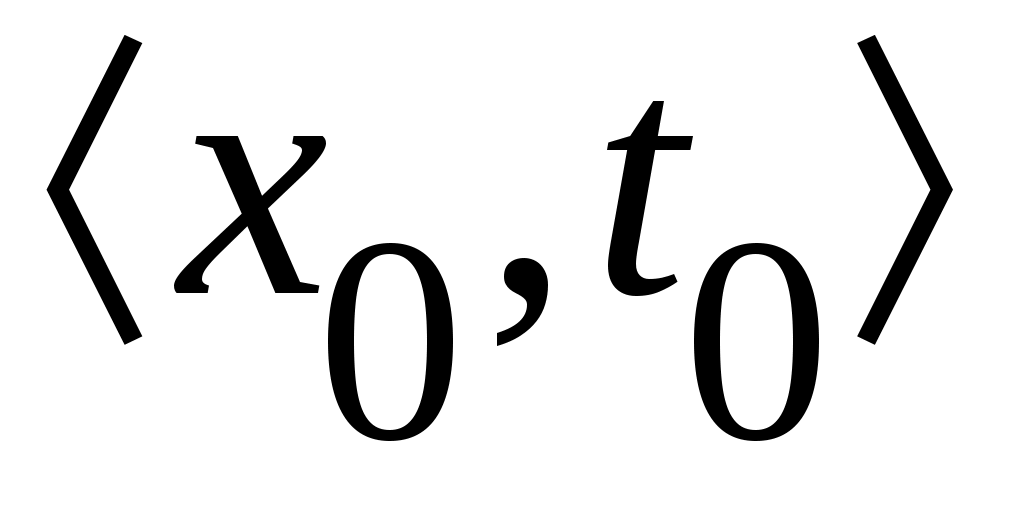 . При этом, подставив вместо состояния . При этом, подставив вместо состояния 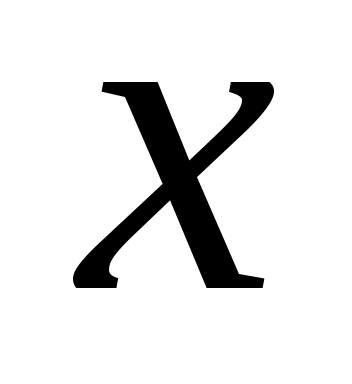 его выражение через начальные условия и время, получим сложную функцию времени, значение которой определяется в виде композиции его выражение через начальные условия и время, получим сложную функцию времени, значение которой определяется в виде композиции 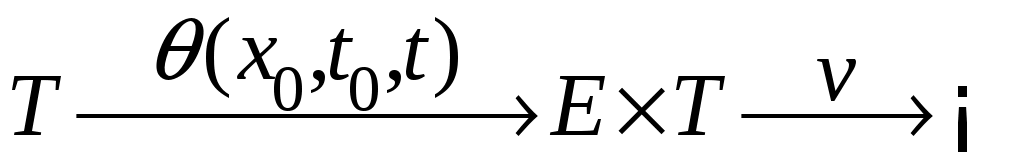 , т.е. в виде , т.е. в виде 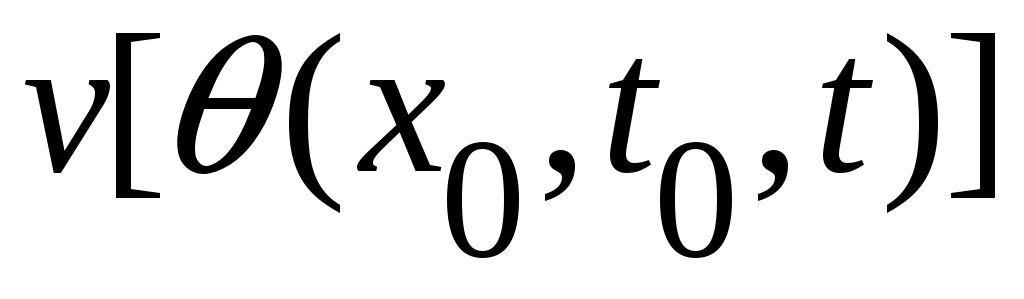 . Убывание (или возрастание) функции . Убывание (или возрастание) функции 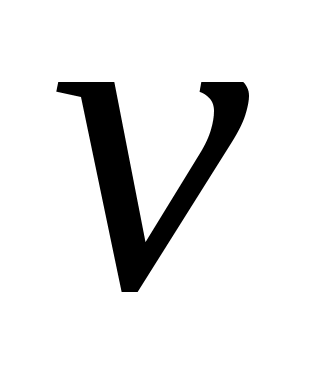 в процессе движения системы определяется знаком ее полной производной по времени в процессе движения системы определяется знаком ее полной производной по времени 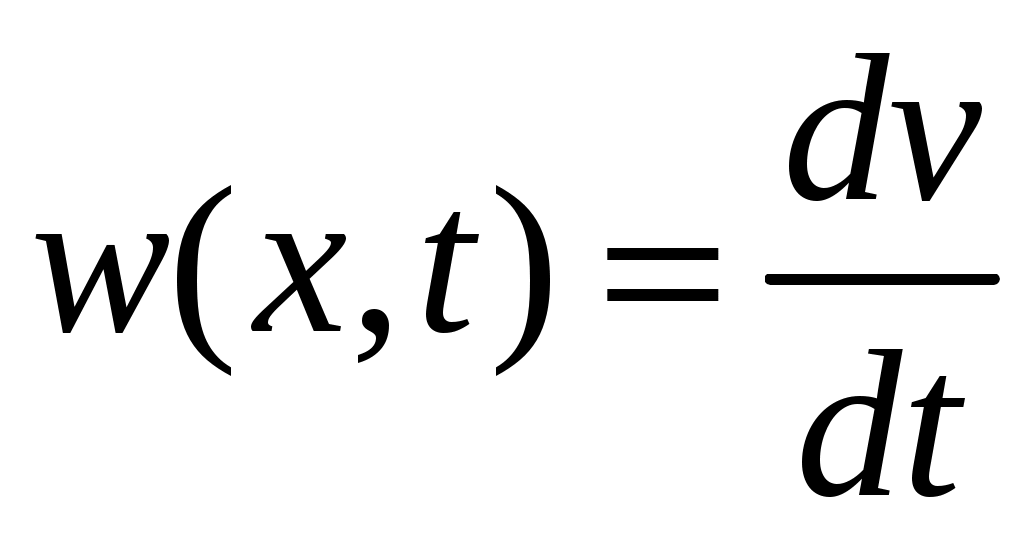 Значения этой производной можно записать в виде Значения этой производной можно записать в виде
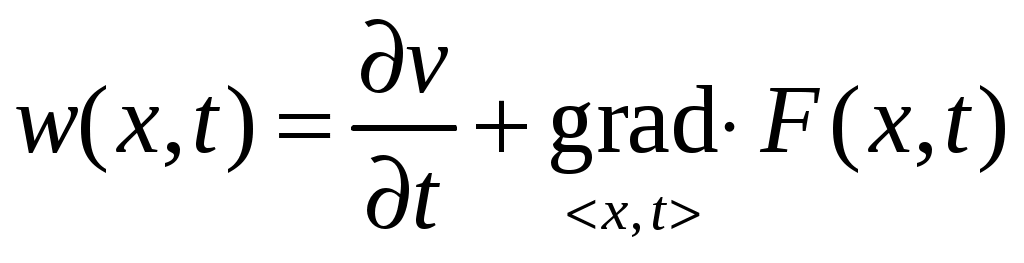 , (1) , (1)
где второе слагаемое представляет собой скалярное произведение градиента функции 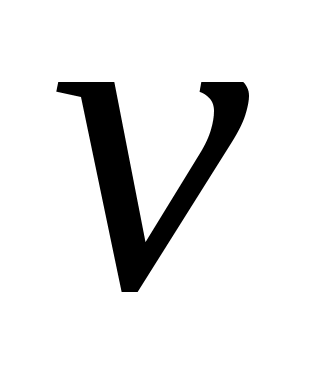 на вектор фазовой скорости, определяемый как правая часть дифференциальных уравнений движения системы в отклонениях. на вектор фазовой скорости, определяемый как правая часть дифференциальных уравнений движения системы в отклонениях.
Функцию 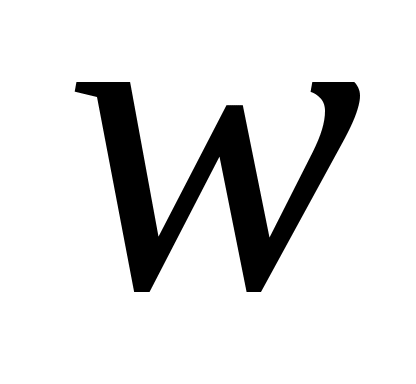 называют обычно полной производной по времени функции называют обычно полной производной по времени функции 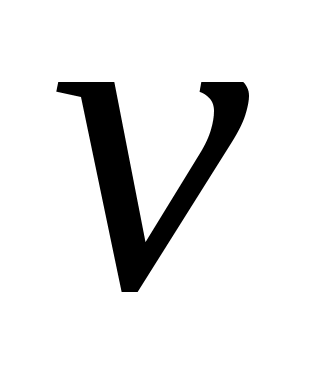 , взятой вдоль вектора фазовой скорости (вдоль траектории движения, в силу уравнений движения). , взятой вдоль вектора фазовой скорости (вдоль траектории движения, в силу уравнений движения).
Для доказательства теорем Ляпунова нам потребуется следующая теорема из математического анализа.
На замкнутом ограниченном подмножестве n-мерного эвклидова пространства (на компакте) непрерывная вещественная функция принимает своё минимальное и максимальное значения.
Теорема об устойчивости.
Теорема 1 (Теорема Ляпунова об устойчивости). Для устойчивости по Ляпунову нулевого состояния равновесия системы в отклонениях достаточно, чтобы существовала такая положительно определенная в окрестности 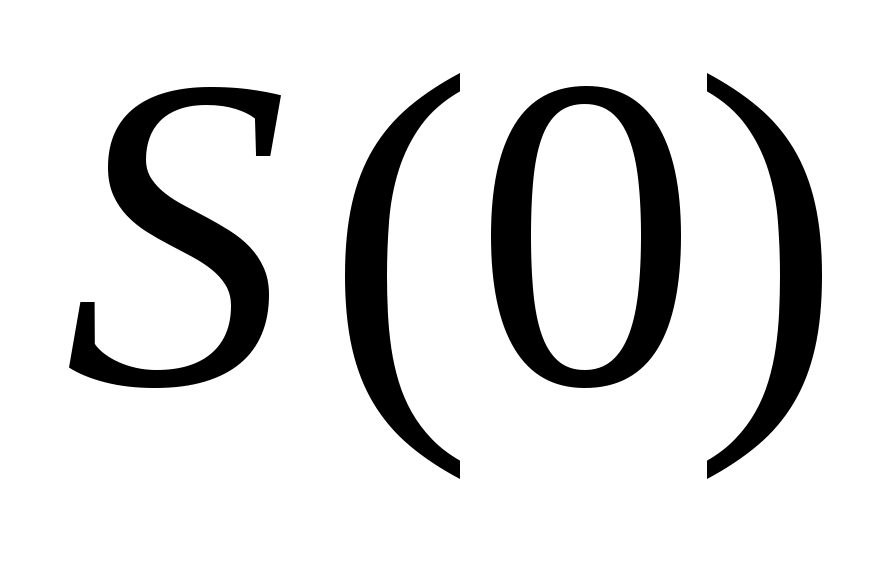 этого состояния равновесия функция этого состояния равновесия функция 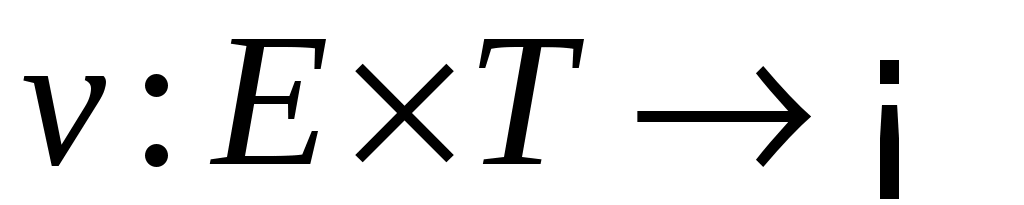 , полная производная которой, взятая в силу уравнений движения, является отрицательно знакопостоянной в окрестности , полная производная которой, взятая в силу уравнений движения, является отрицательно знакопостоянной в окрестности 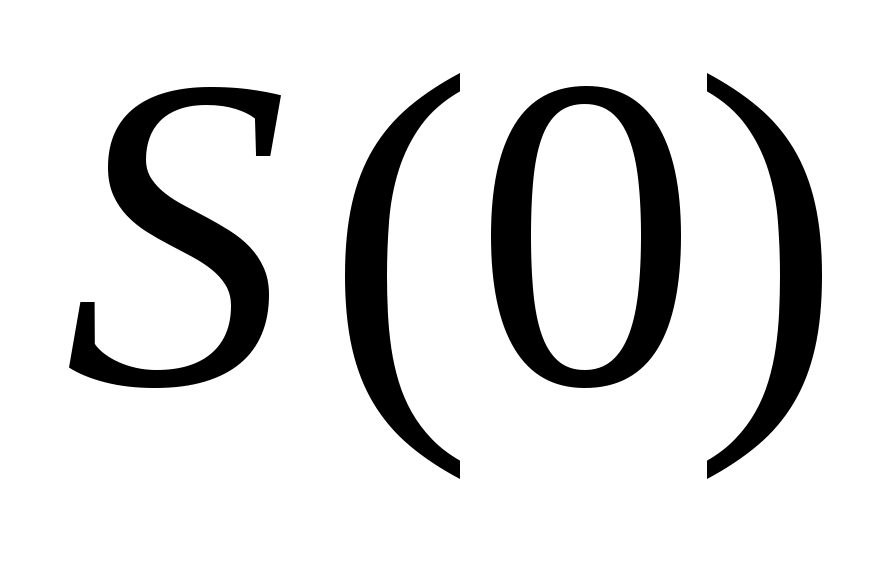 функцией. функцией.
Если эта производная является знакоопределенной в 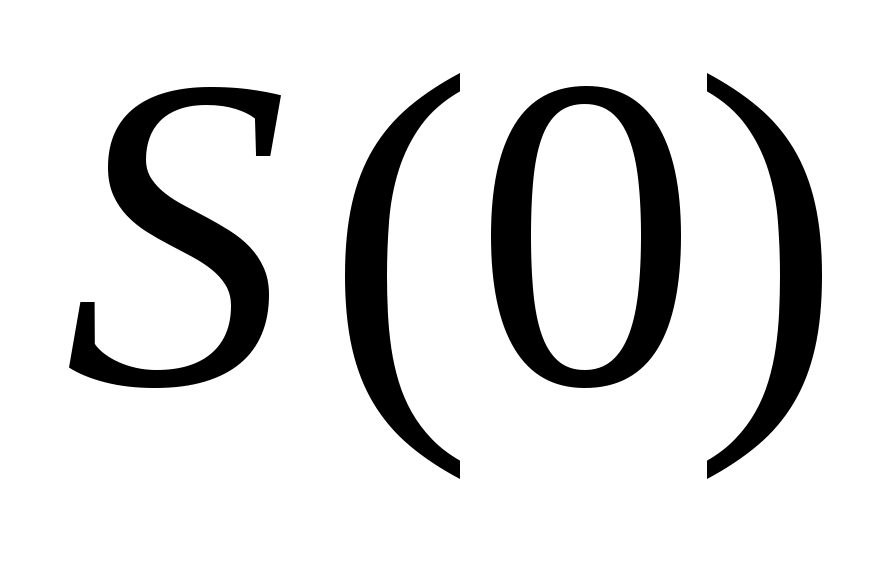 функцией, то нулевое состояние равновесия асимптотически устойчиво по Ляпунову. функцией, то нулевое состояние равновесия асимптотически устойчиво по Ляпунову.
Если, кроме того, функция 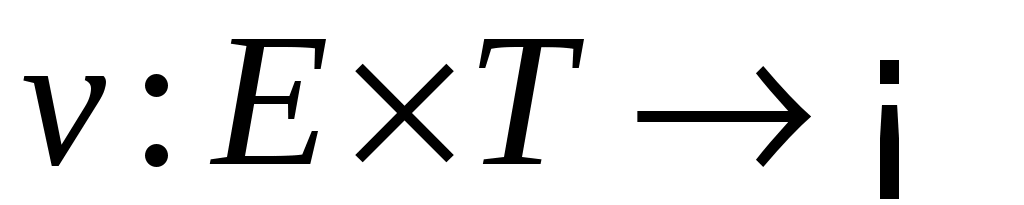 равномерно непрерывна по равномерно непрерывна по 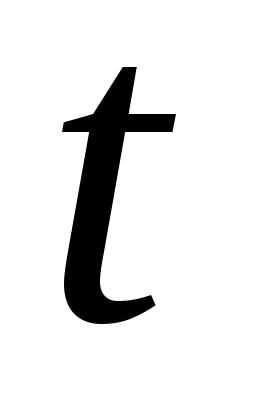 , то устойчивость нулевого состояния равновесия равномерна. , то устойчивость нулевого состояния равновесия равномерна.
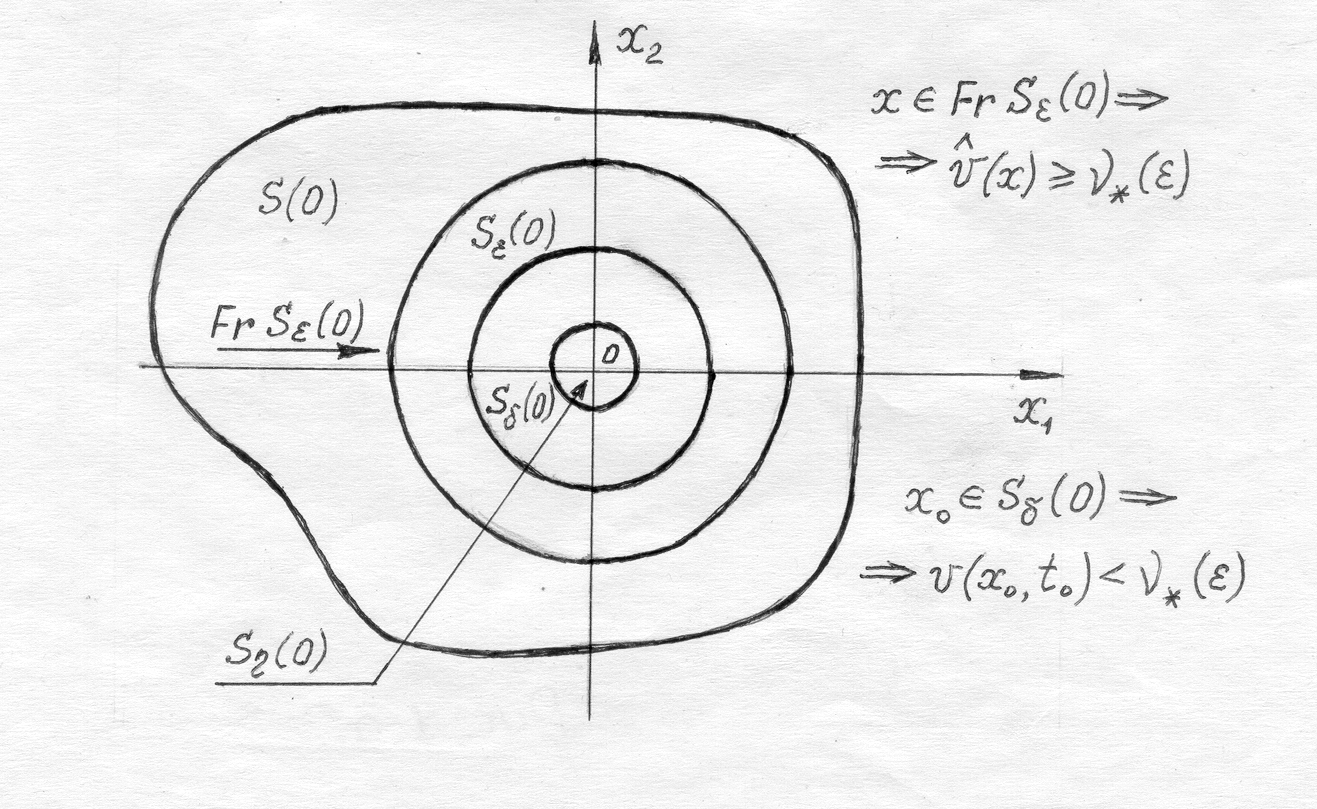
Если 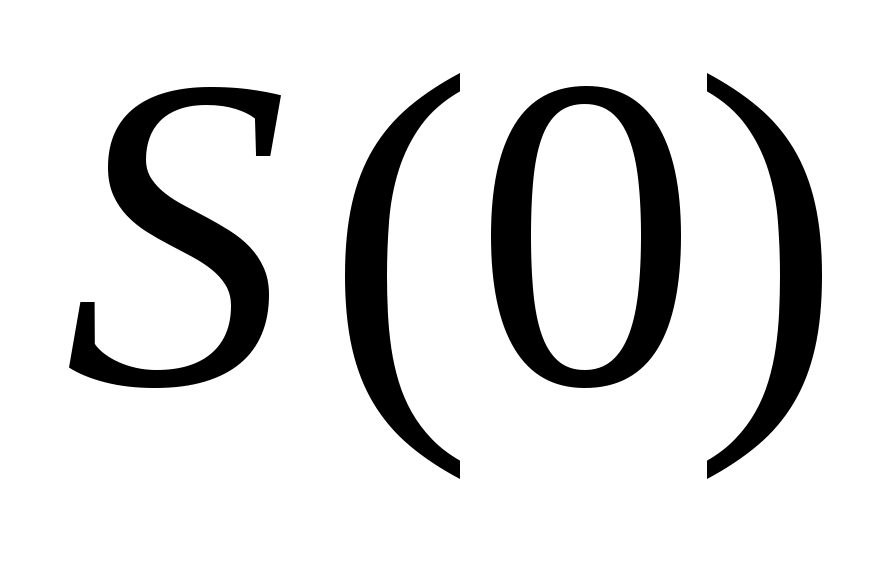 - окрестность, в которой функция - окрестность, в которой функция 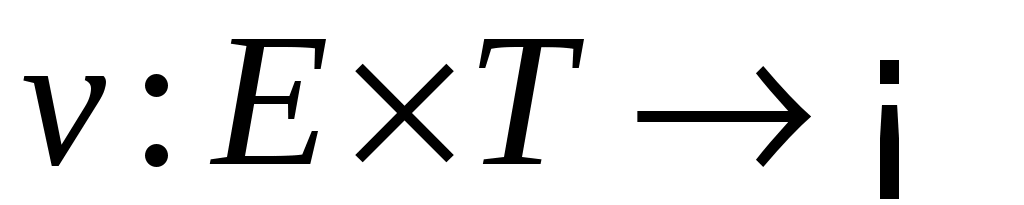 положительно определена, то обозначим через положительно определена, то обозначим через 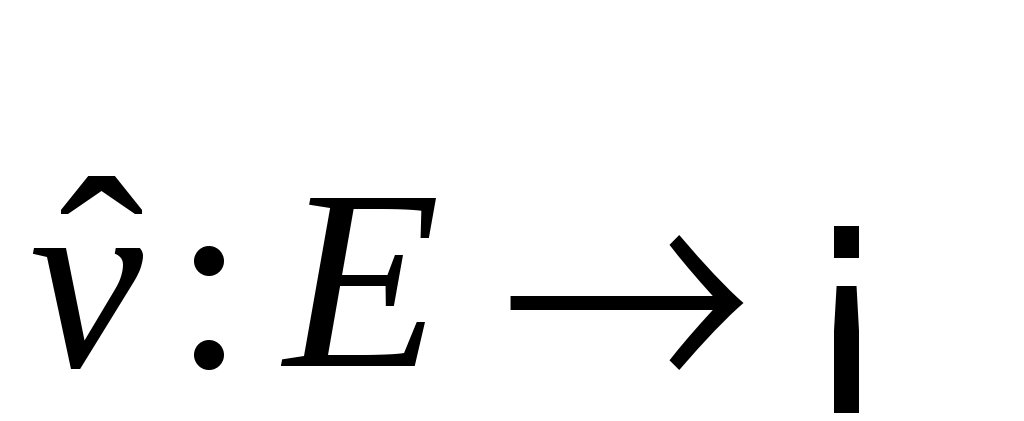 знакоопределенную положительную функцию, мажорируемую функцией знакоопределенную положительную функцию, мажорируемую функцией 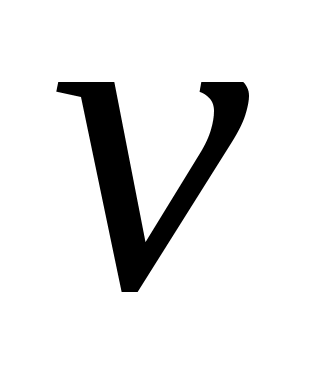 , так что , так что 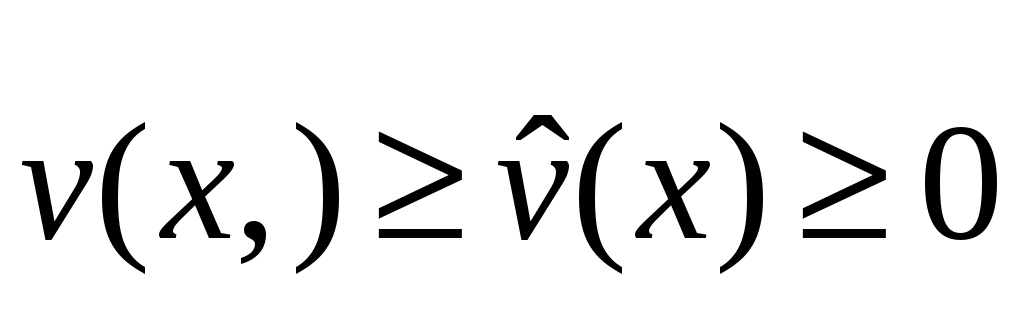 для всех для всех 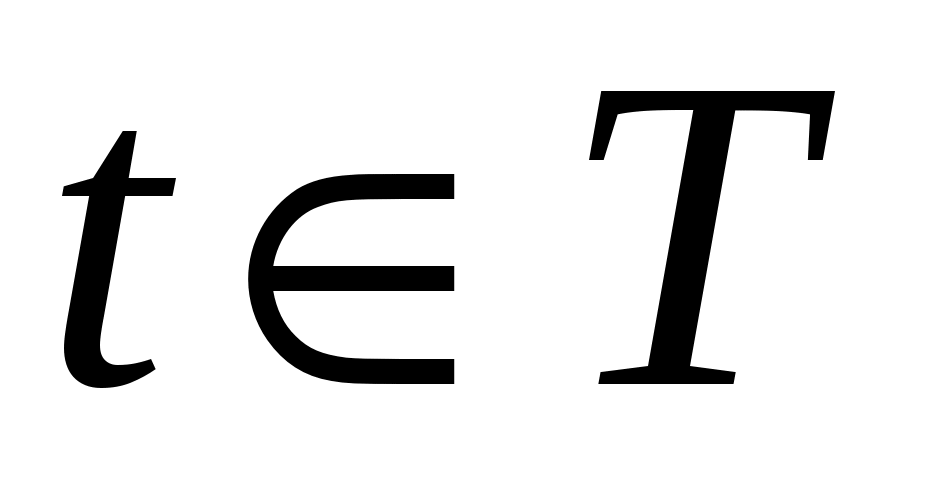 и и 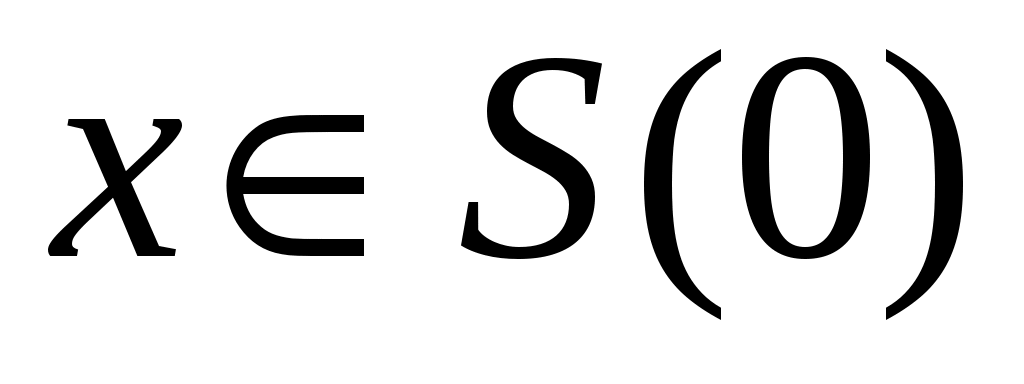 . Граница . Граница 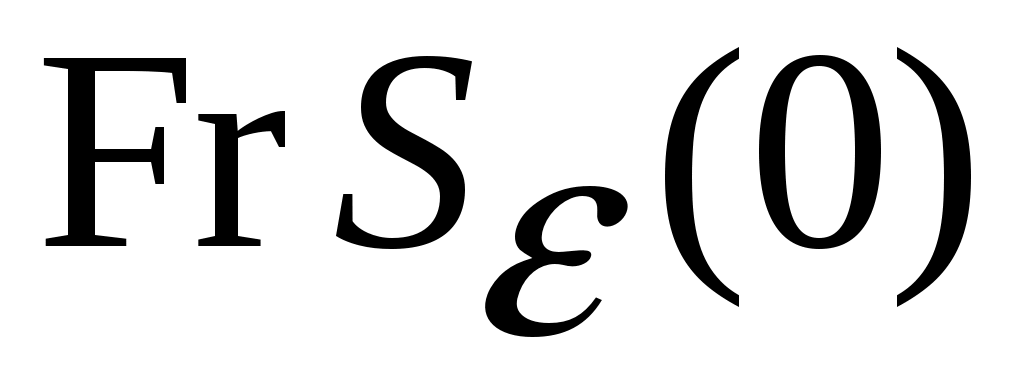 окрестности окрестности 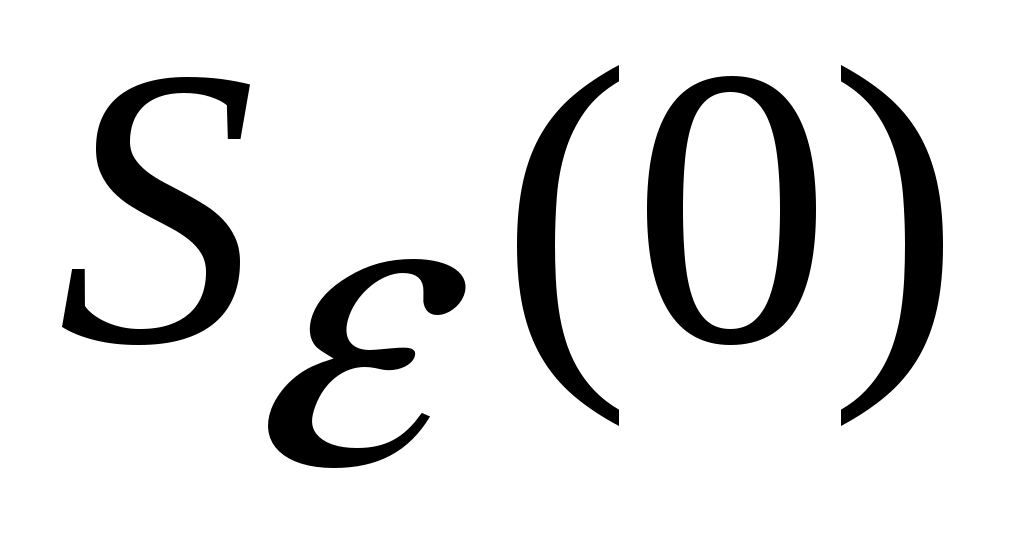 является замкнутым ограниченным множеством (компактом), на котором функция является замкнутым ограниченным множеством (компактом), на котором функция 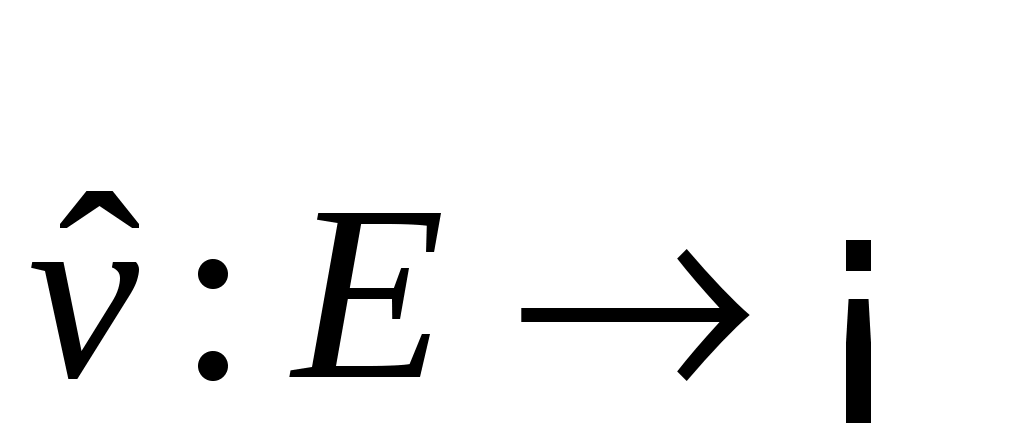 принимает свое минимальное значение принимает свое минимальное значение 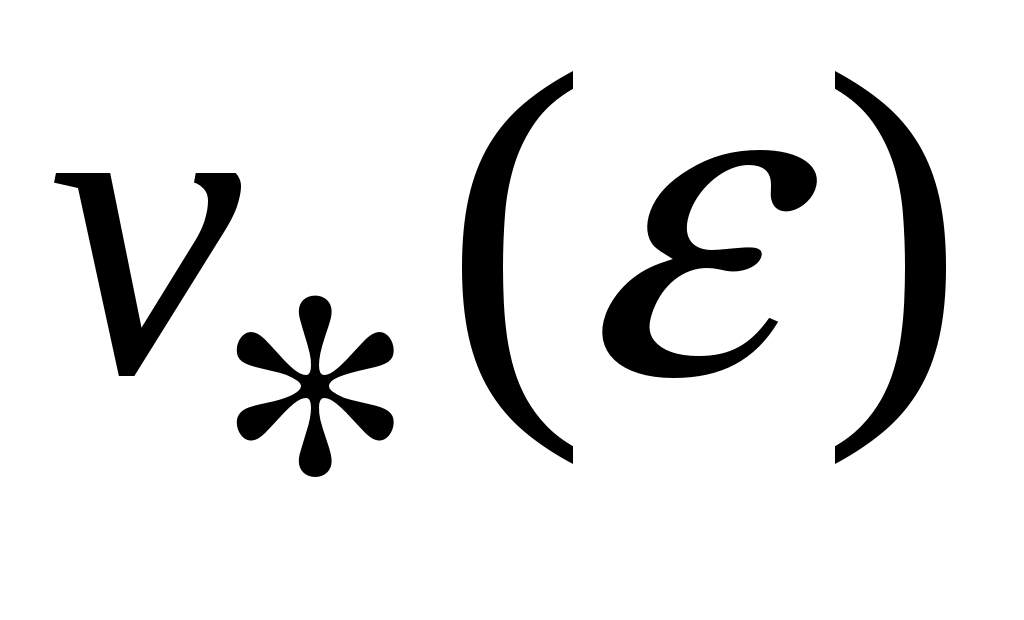 . .
Так как 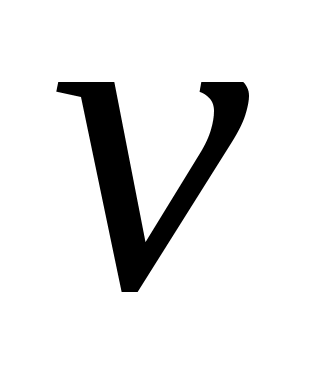 непрерывна и равна нулю в точке 0, то для любого непрерывна и равна нулю в точке 0, то для любого 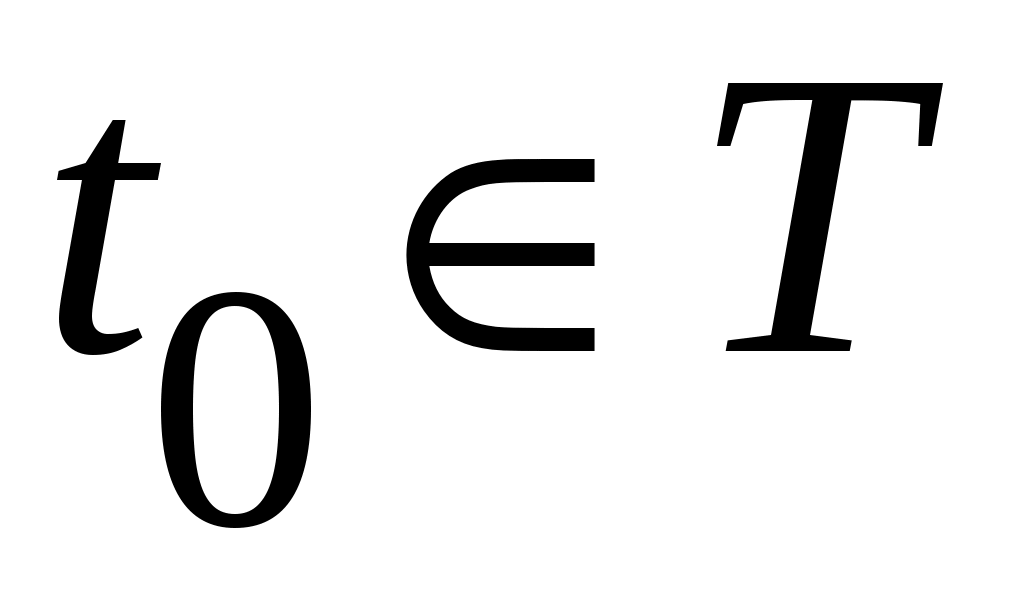 и любого и любого 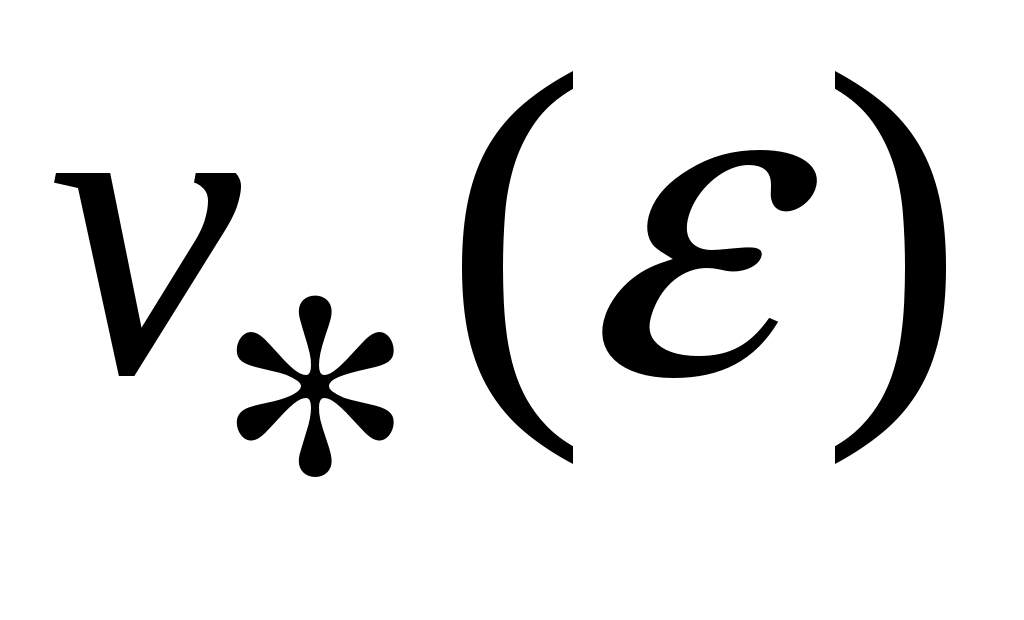 можно найти такое можно найти такое 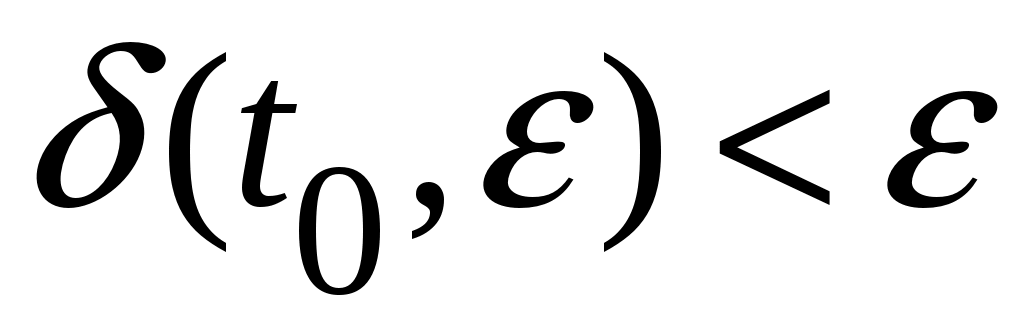 , что , что 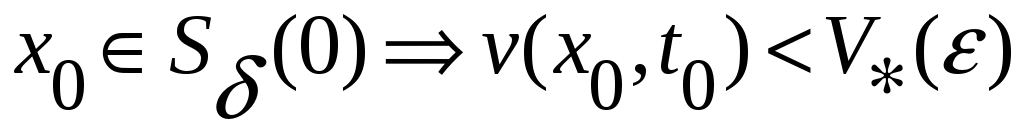 . Рассмотрим теперь начинающееся в точке . Рассмотрим теперь начинающееся в точке 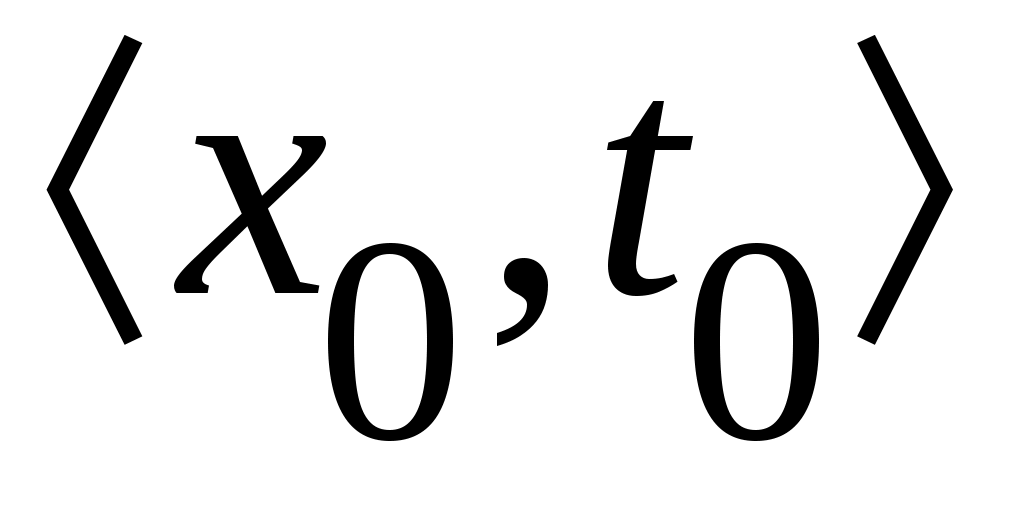 движение и запишем, как будет изменяться значение функции движение и запишем, как будет изменяться значение функции 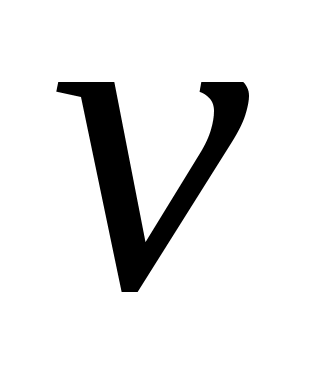 , если ее аргумент , если ее аргумент 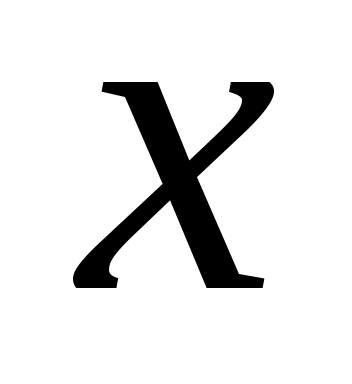 менять со временем в соответствии с изменением состояния в процессе движения. Имеем: менять со временем в соответствии с изменением состояния в процессе движения. Имеем:
 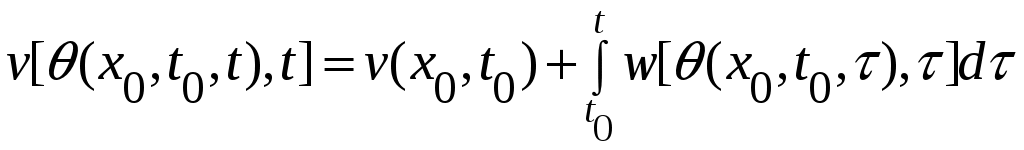 , (2) , (2)
где стоящая под знаком интеграла функция 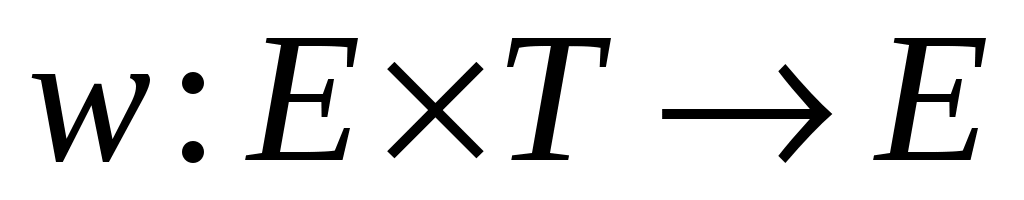 является полной производной по времени функции является полной производной по времени функции 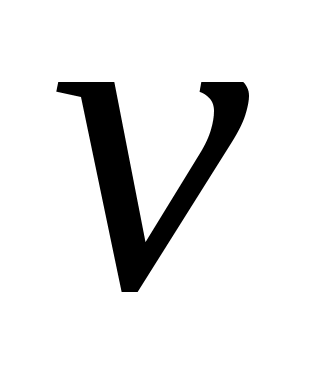 , взятой в силу уравнений движения. Так как по условию теоремы функция , взятой в силу уравнений движения. Так как по условию теоремы функция 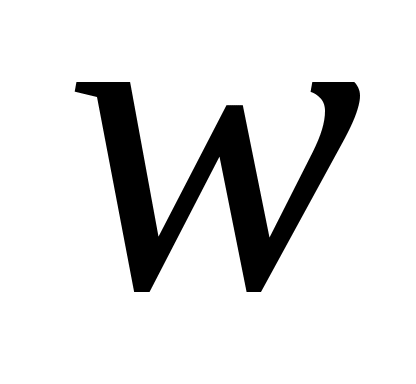 в окрестности в окрестности 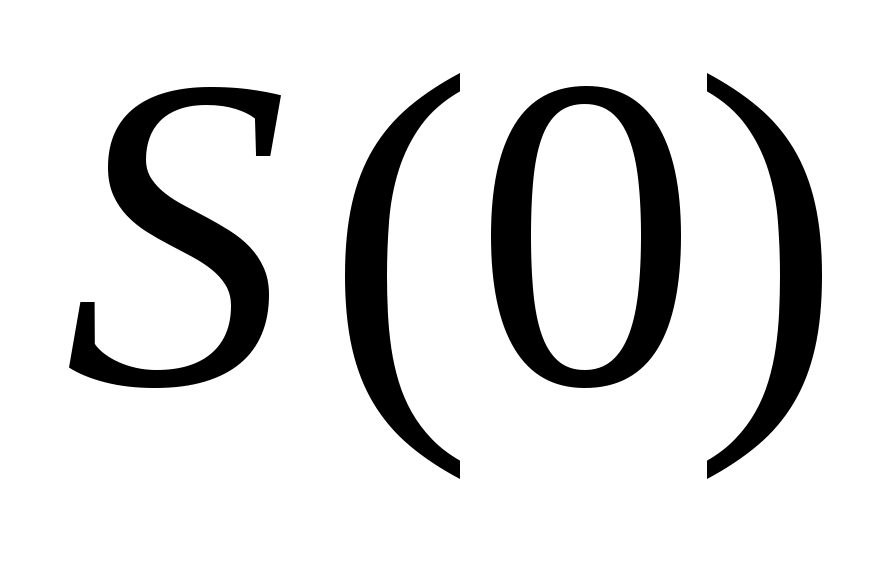 (и, следовательно, (и, следовательно, 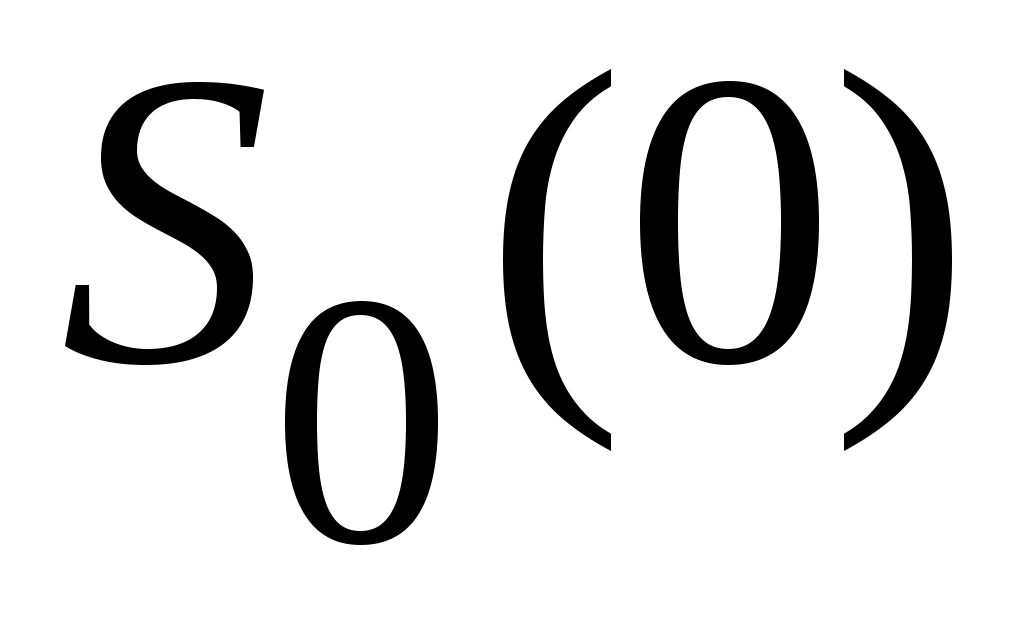 ) неположительна, то для любых ) неположительна, то для любых 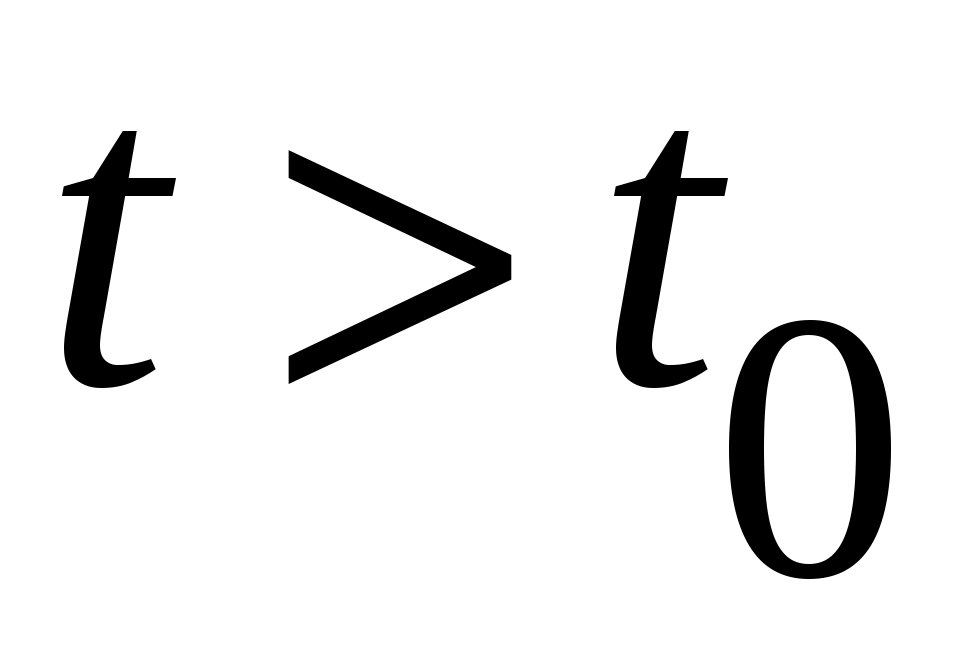 справедливо неравенство справедливо неравенство 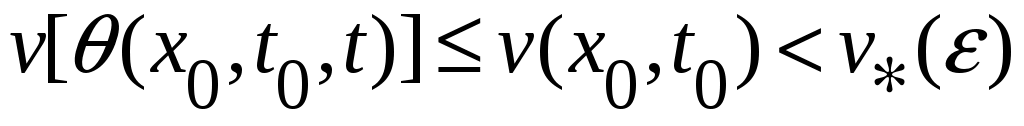 для любых для любых 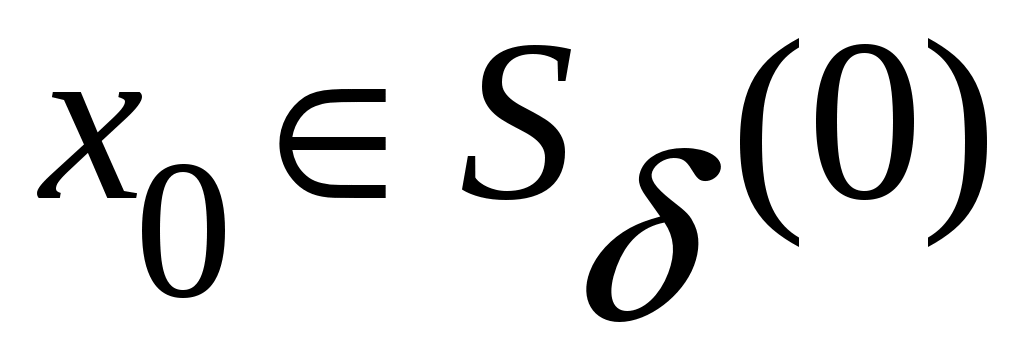 . Но ввиду того, что на границе . Но ввиду того, что на границе 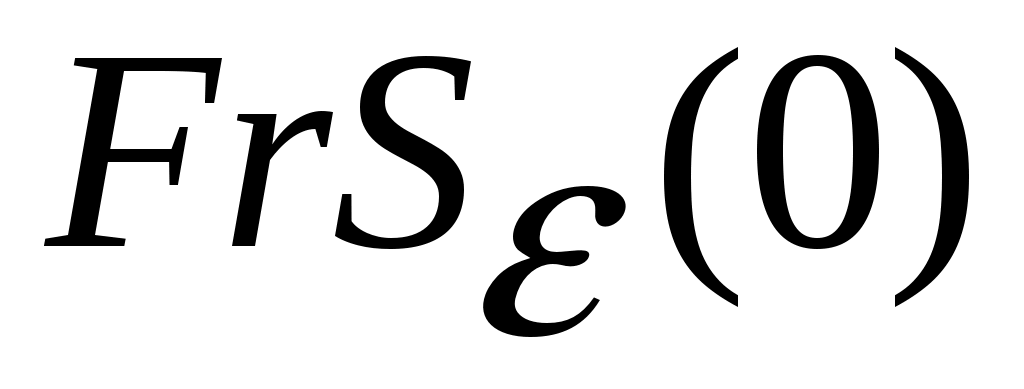 окрестности окрестности 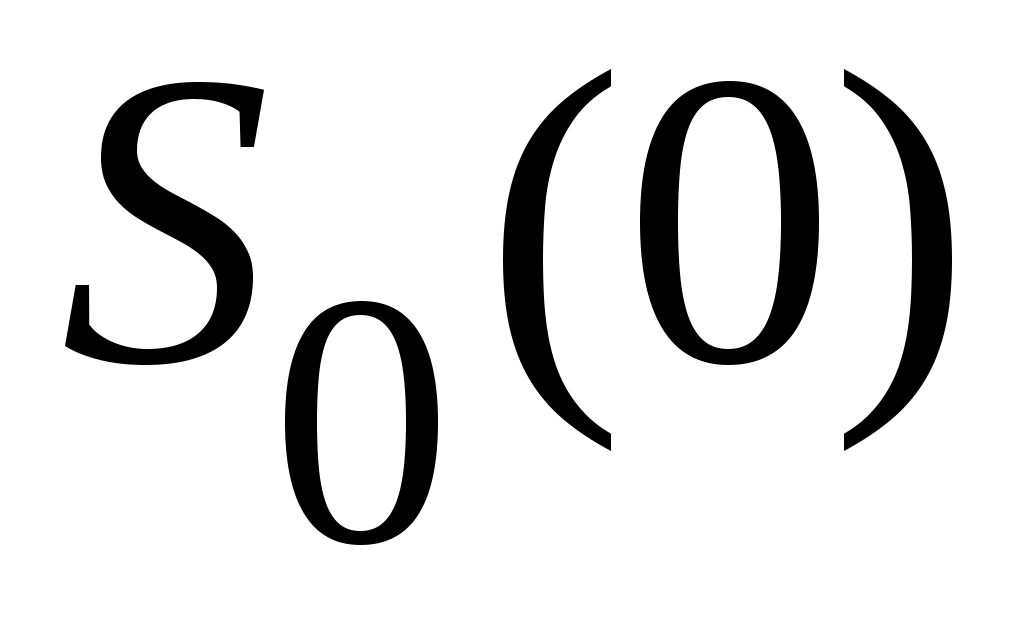 непрерывная функция непрерывная функция  , движение системы ни при каких , движение системы ни при каких  не может достичь границы не может достичь границы  окрестности окрестности 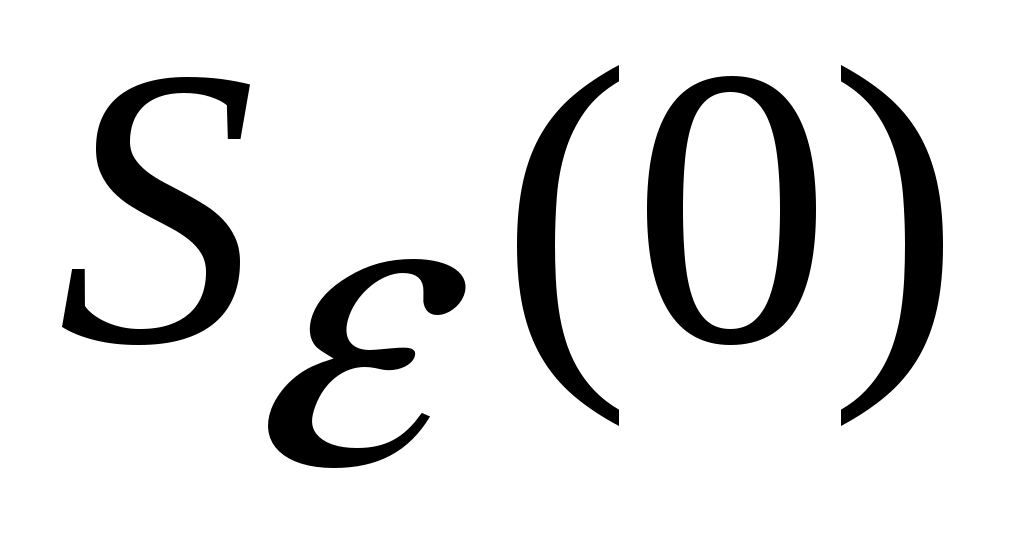 , и, следовательно, состояние системы не выйдет за пределы этой окрестности при начальных условиях , и, следовательно, состояние системы не выйдет за пределы этой окрестности при начальных условиях 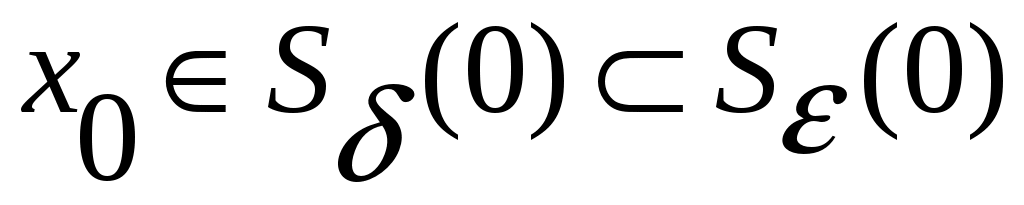 , что доказывает факт устойчивости по Ляпунову нулевого состояния равновесия. , что доказывает факт устойчивости по Ляпунову нулевого состояния равновесия.
Для доказательства асимптотической устойчивости достаточно показать, что для любого 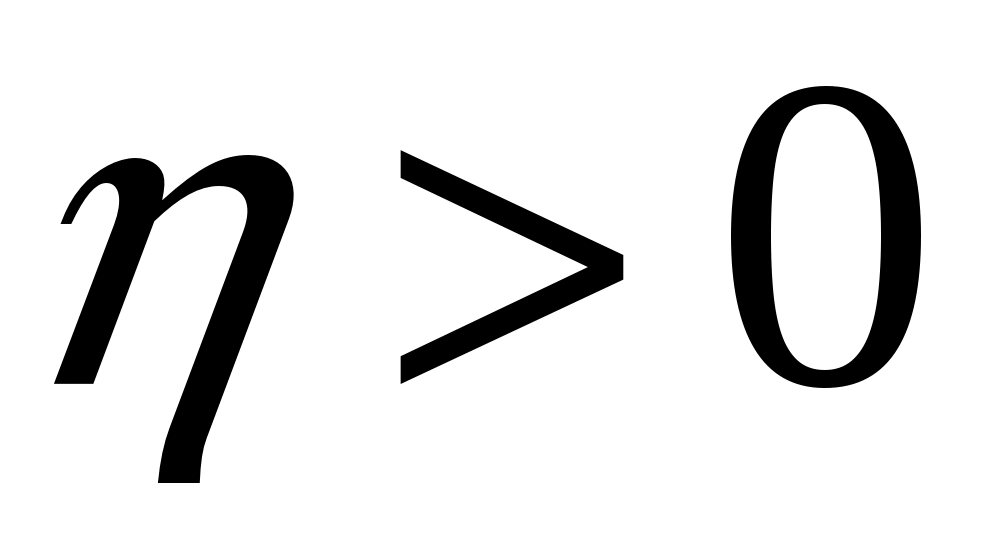 движение системы, начавшееся в окрестности движение системы, начавшееся в окрестности 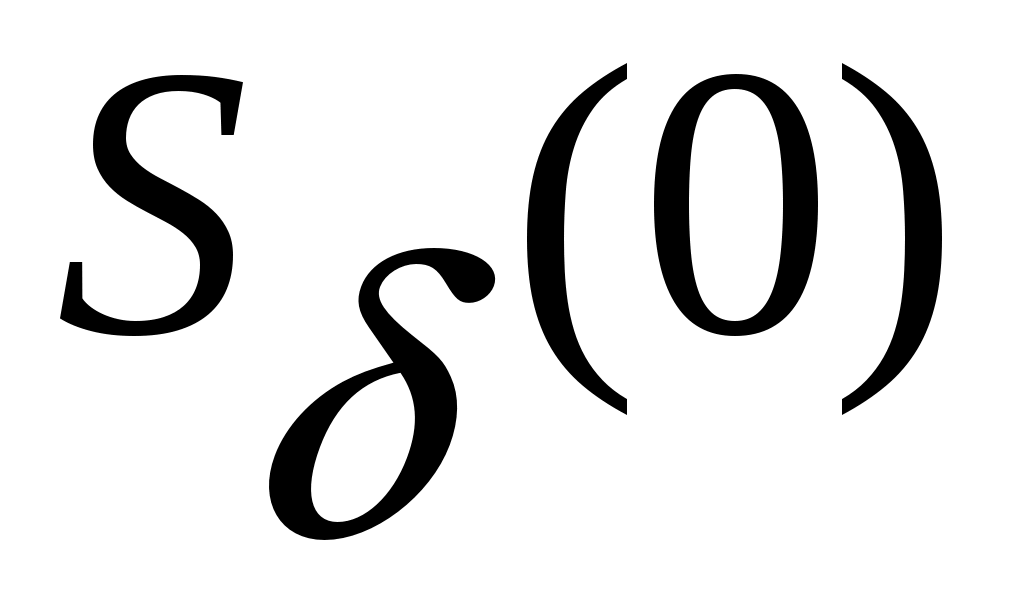 за конечное время достигнет окрестности за конечное время достигнет окрестности 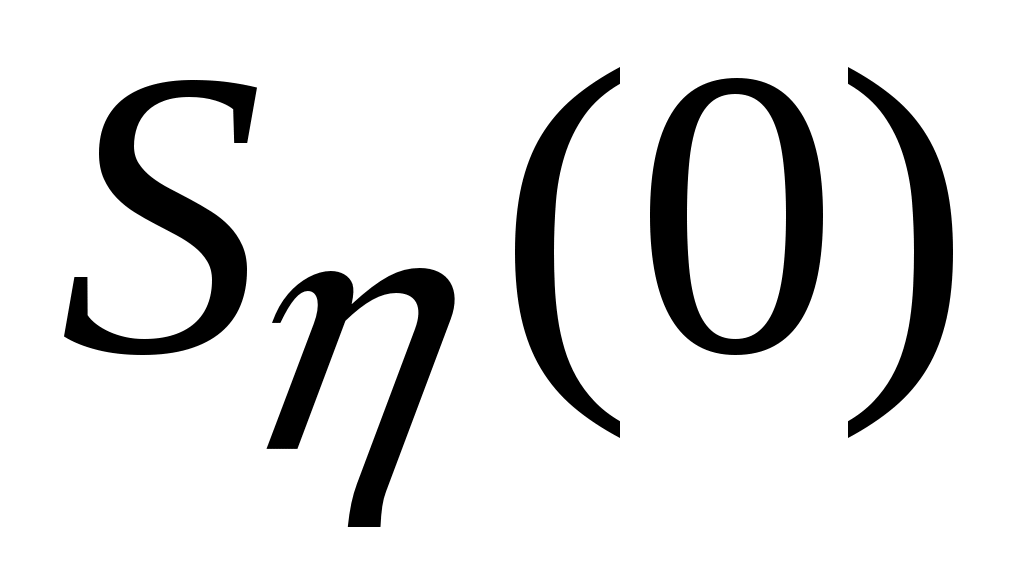 . .
Предположим противное. В этом случае найдется такое 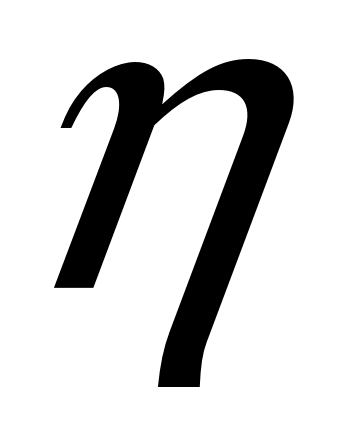 , что для всех , что для всех 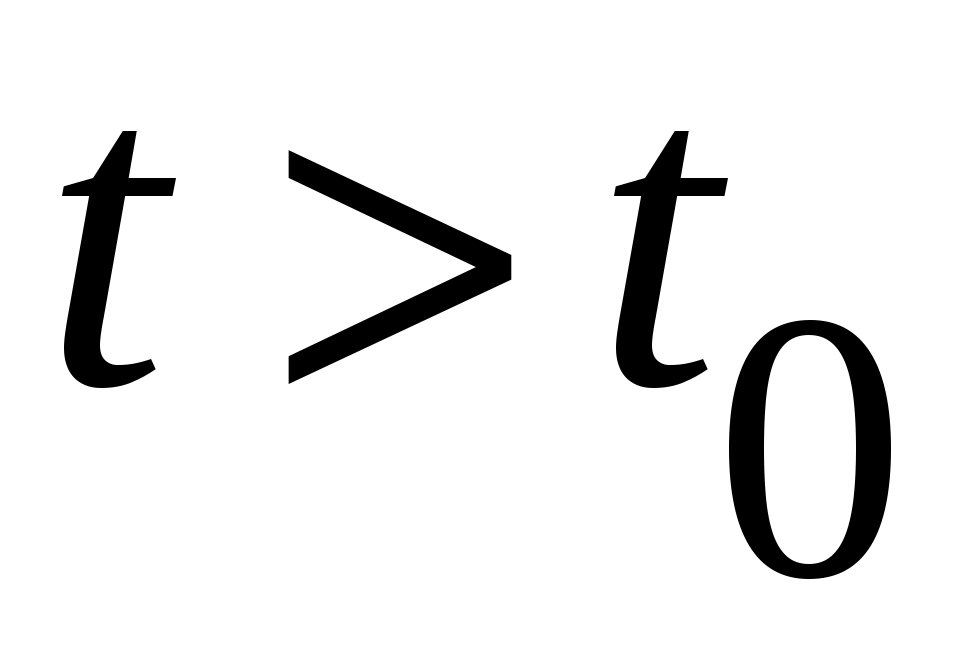 состояние системы состояние системы 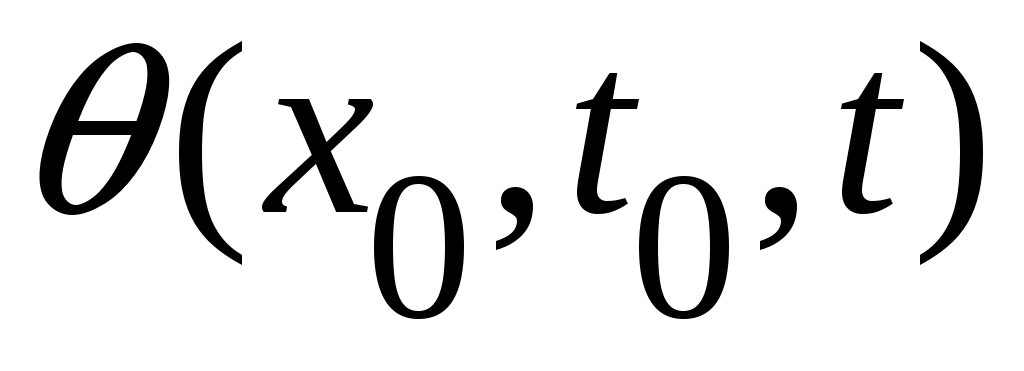 , движение которой начинается в , движение которой начинается в 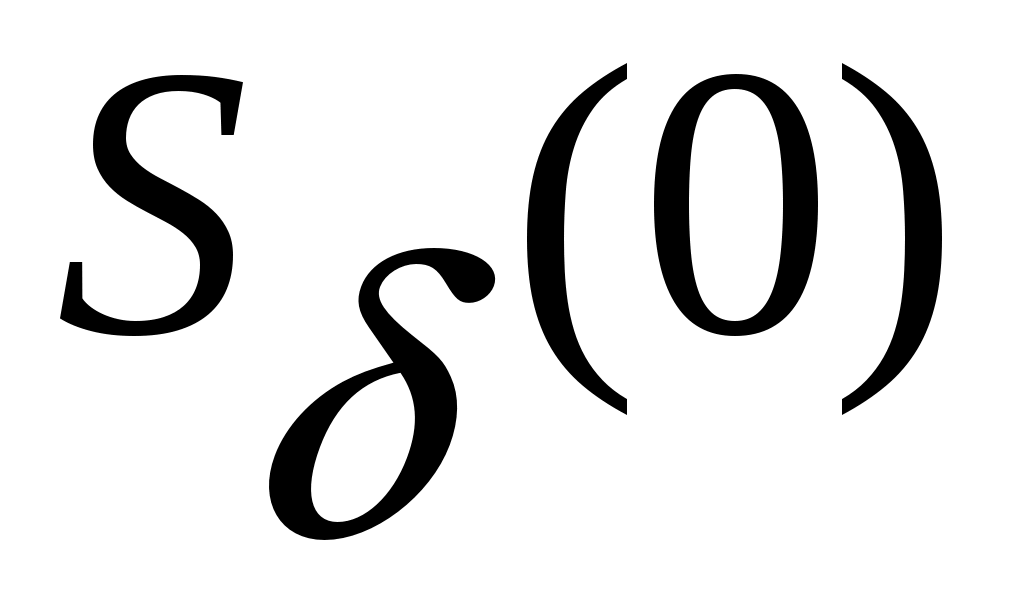 , при , при 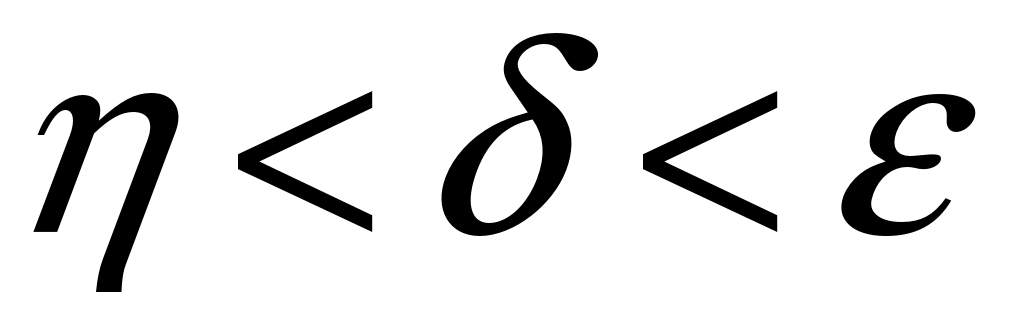 останется в пределах кольцевого компактного множество останется в пределах кольцевого компактного множество 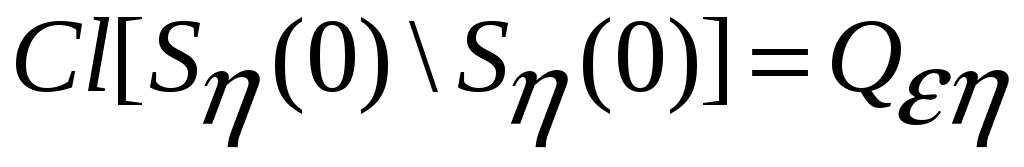 . .
На компакте 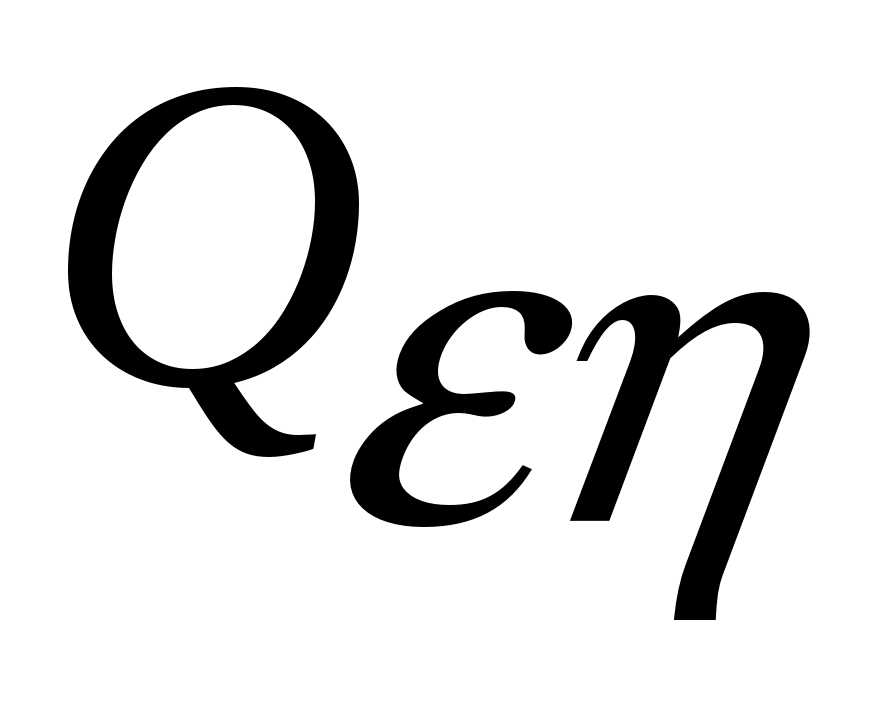 производная функции производная функции 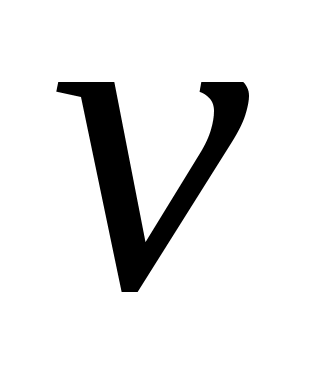 будет, по условию, знакоопределенной отрицательной функцией, и, следовательно, найдется такая отрицательная знакоопределенная функция будет, по условию, знакоопределенной отрицательной функцией, и, следовательно, найдется такая отрицательная знакоопределенная функция 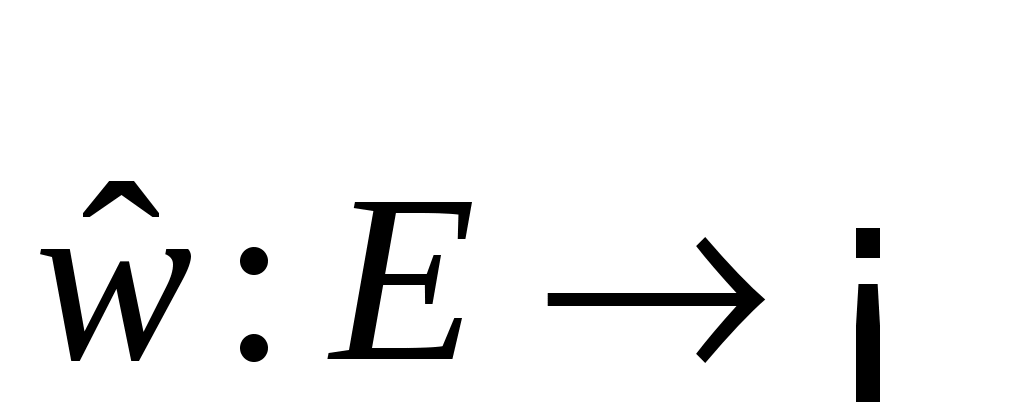 , что , что 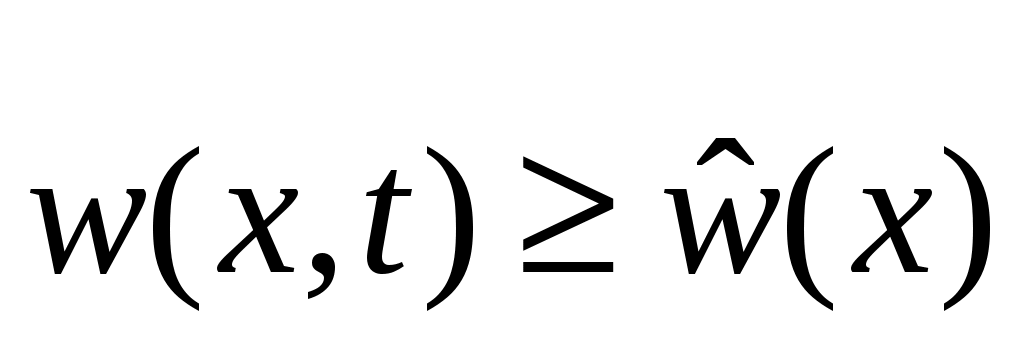 для всех для всех 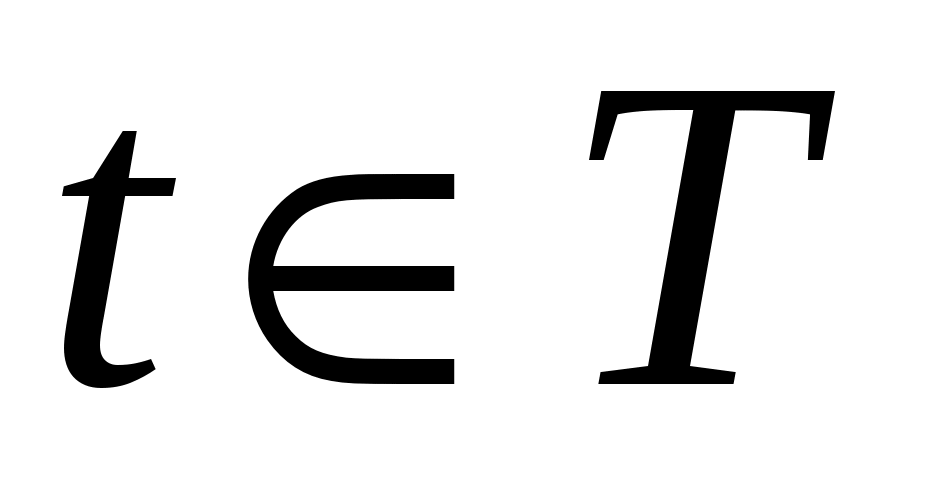 . На компакте . На компакте 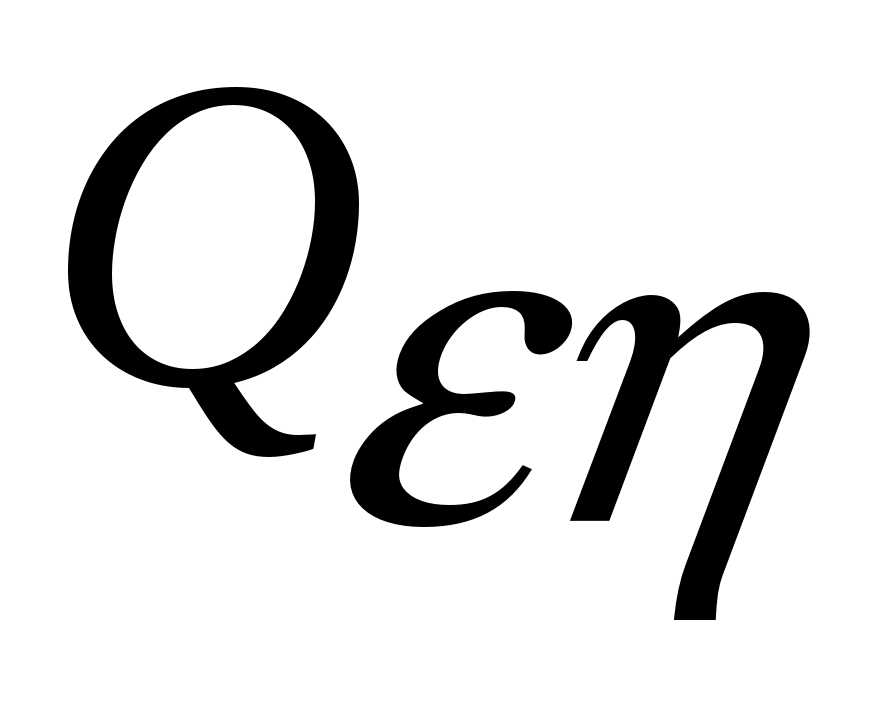 функция функция  будет принимать свое максимальное значение будет принимать свое максимальное значение 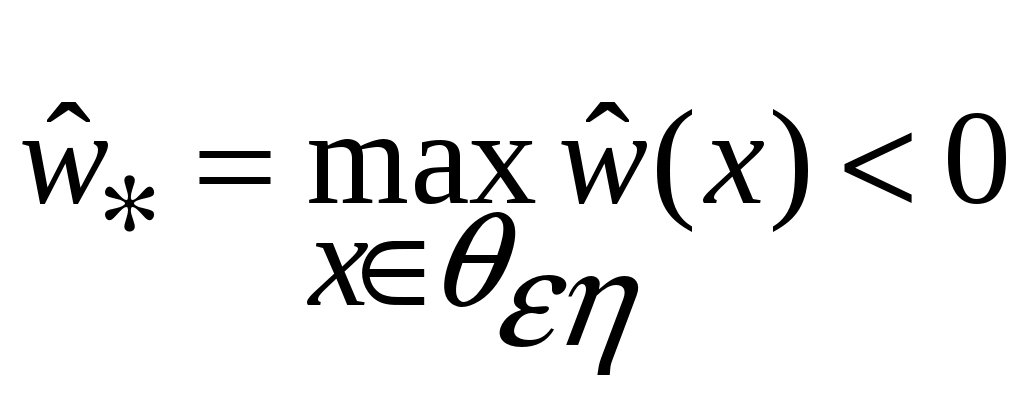 . При этом из (2) будет следовать на основании теоремы о среднем неравенство: . При этом из (2) будет следовать на основании теоремы о среднем неравенство: 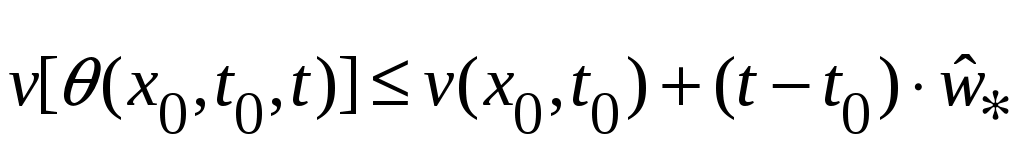 , которое означает, что при , которое означает, что при 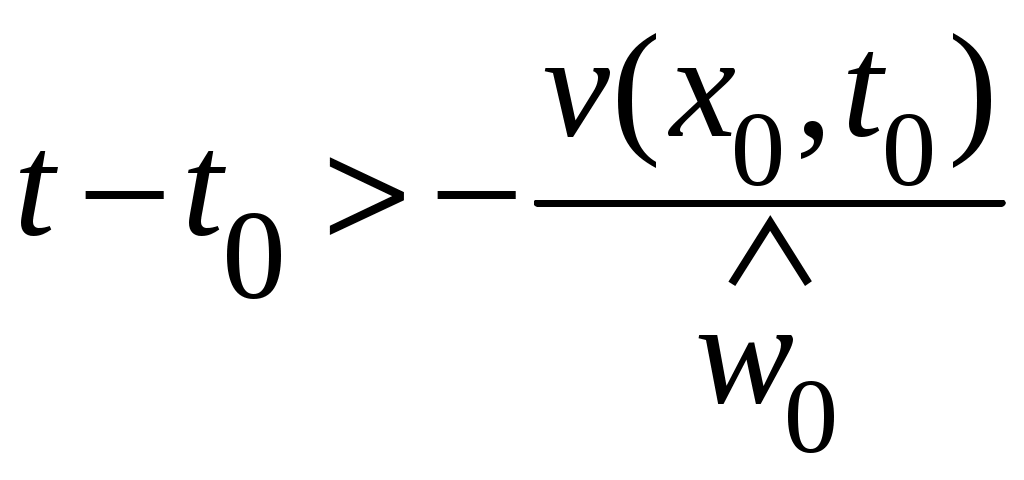 функция функция 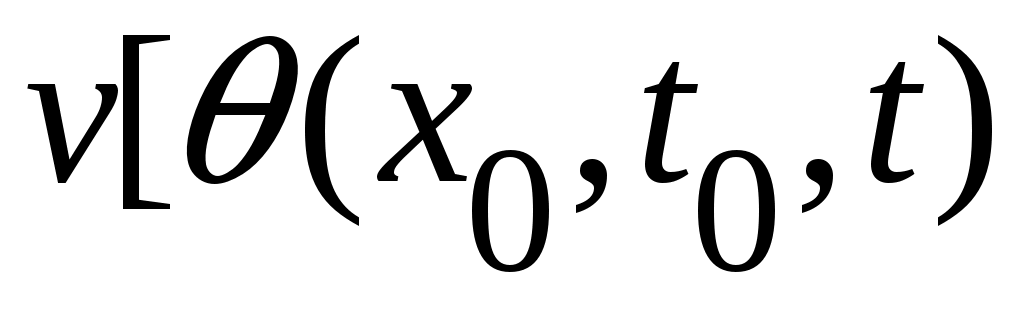 становится отрицательной в некоторых точках становится отрицательной в некоторых точках 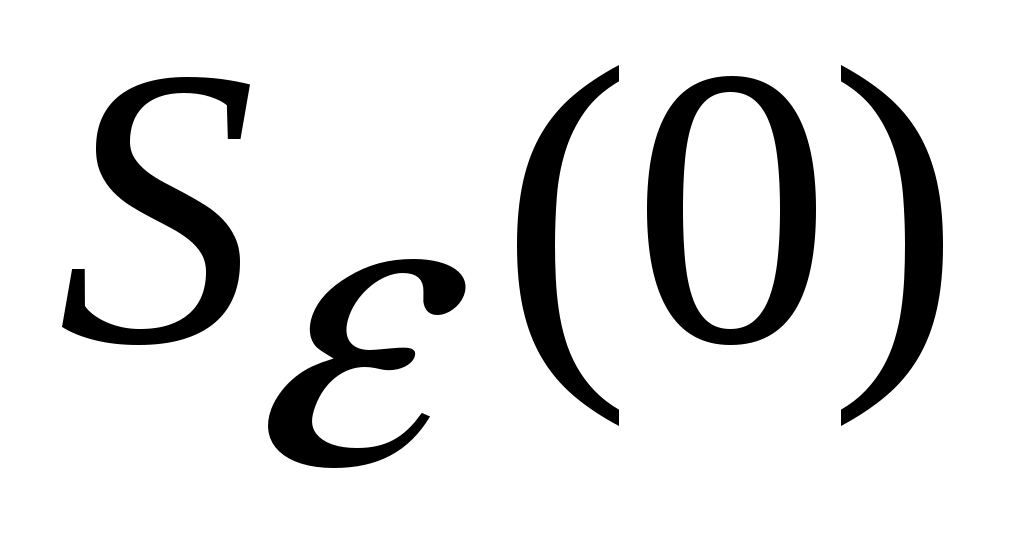 . Полученное противоречие с оговоренной в условии положительной определенностью функции . Полученное противоречие с оговоренной в условии положительной определенностью функции 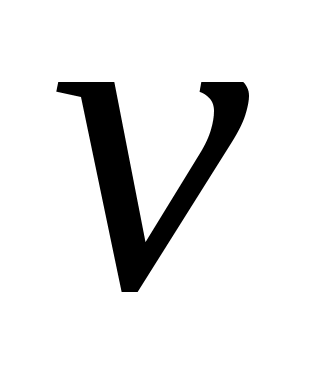 в окрестности в окрестности 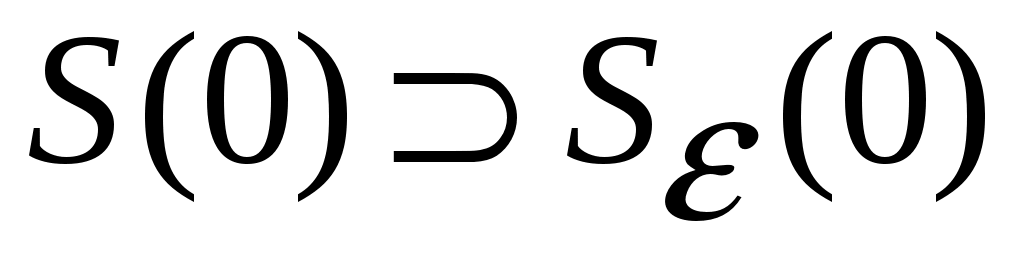 завершает доказательство асимптотической устойчивости движения. завершает доказательство асимптотической устойчивости движения.
Утверждение относительно равномерной устойчивости очевидно, т.к. выполнение условий о равномерной непрерывности 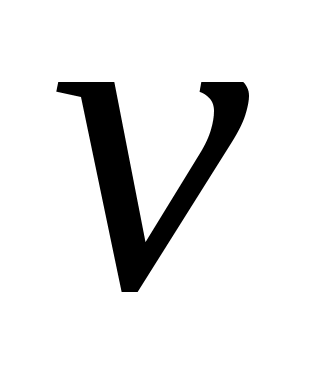 по по 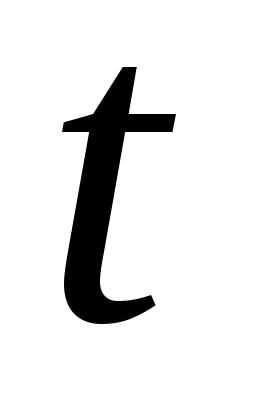 означает, что число означает, что число 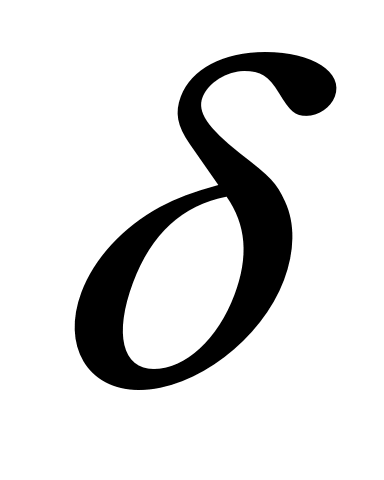 , фигурирующее в доказательстве теоремы, можно выбирать независимо от начала отсчета , фигурирующее в доказательстве теоремы, можно выбирать независимо от начала отсчета 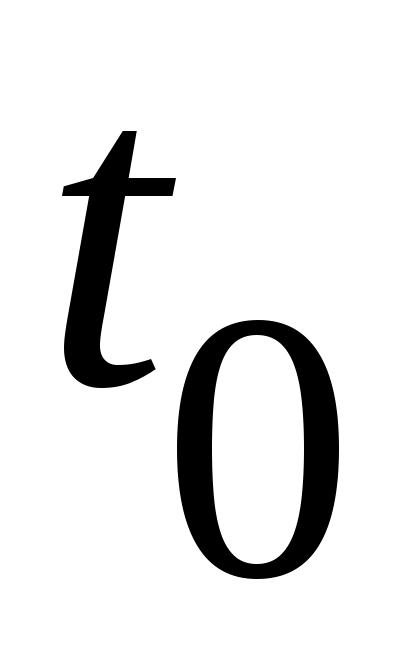 . .
Теорема о неустойчивости
Теорема 2 (Теорема Ляпунова о неустойчивости). Для неустойчивости по Ляпунову нулевого состояния равновесия системы в отклонениях достаточно, чтобы существовала такая равномерно непрерывная по 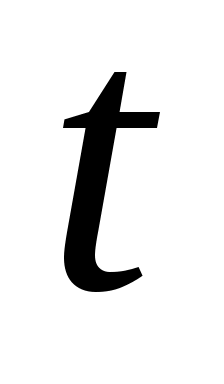 равная нулю в начале координаты непрерывно дифференцируемая функция, принимающая как угодно близко от точки 0 положительные значения, производная которой равная нулю в начале координаты непрерывно дифференцируемая функция, принимающая как угодно близко от точки 0 положительные значения, производная которой 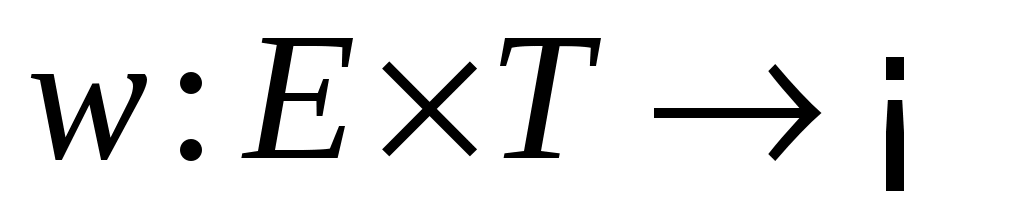 является знакоопределенной положительной в окрестности является знакоопределенной положительной в окрестности 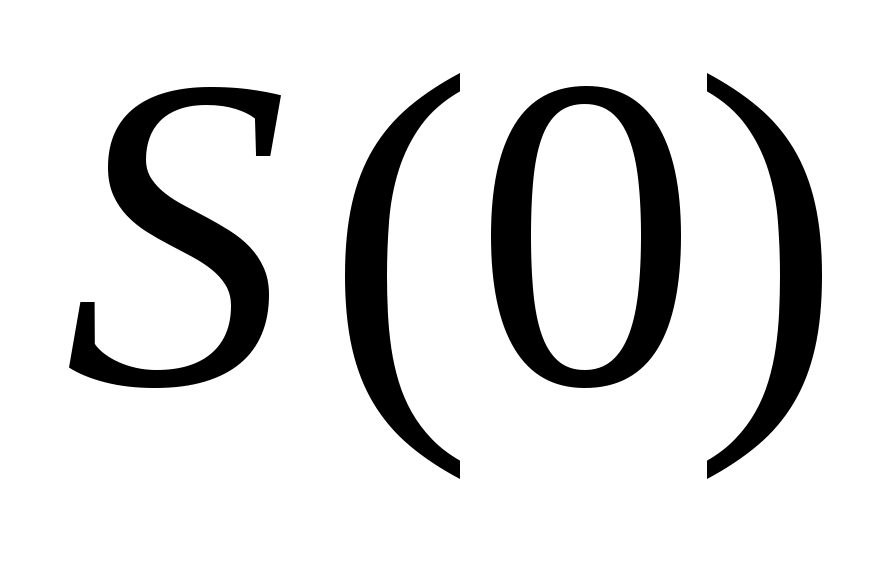 функцией. функцией.
Обозначим через 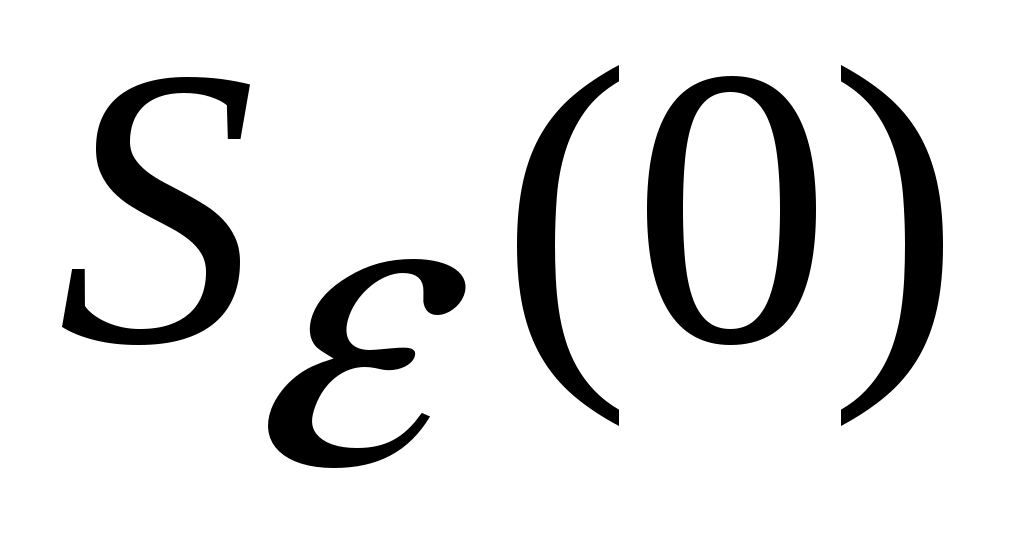 окрестности нулевого состояния равновесия, целиком лежащую в окрестности нулевого состояния равновесия, целиком лежащую в 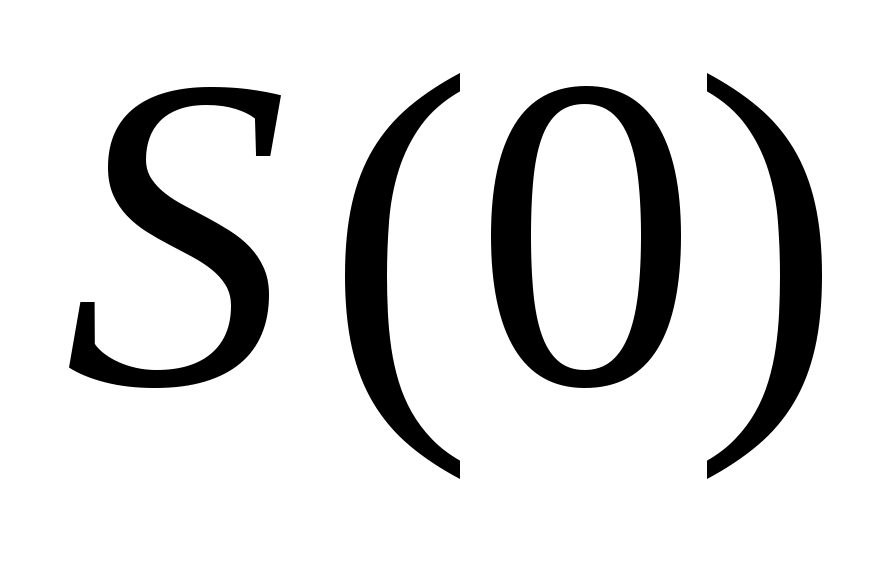 . Для любого . Для любого 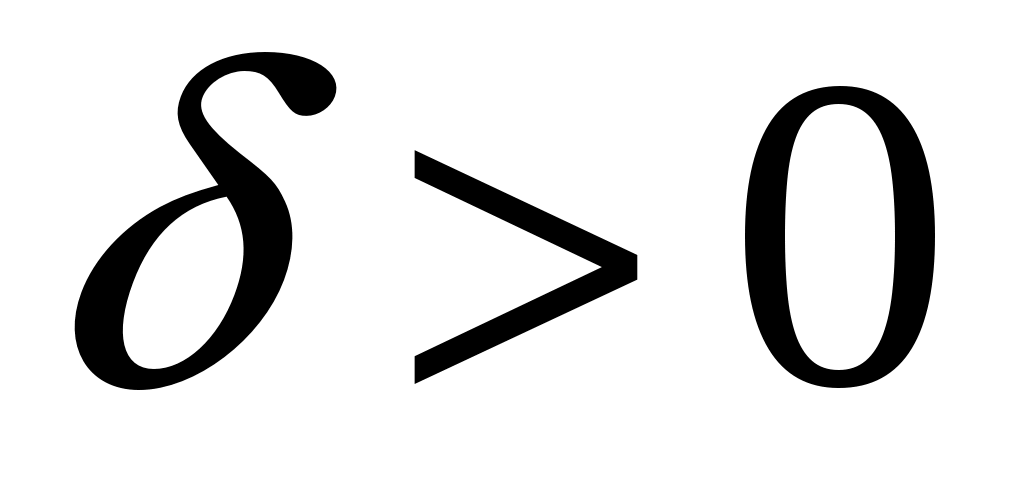 найдется такая точка найдется такая точка 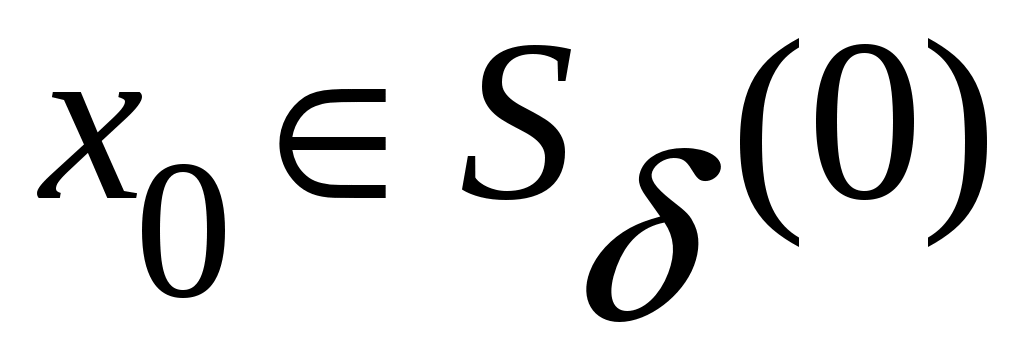 , что , что 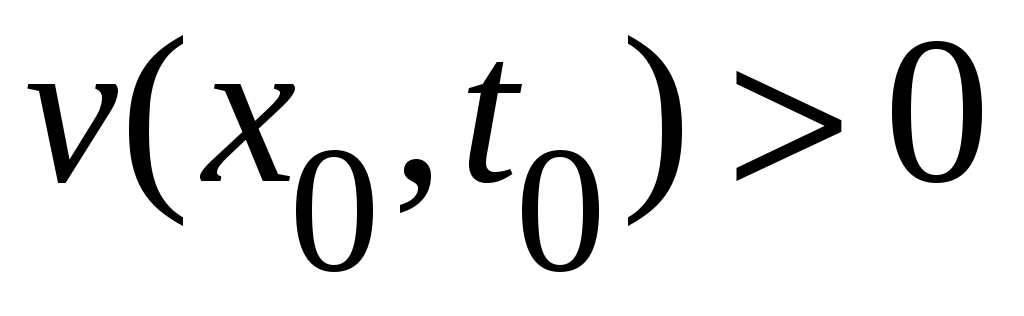 . Тогда, в силу равномерной непрерывности функции . Тогда, в силу равномерной непрерывности функции 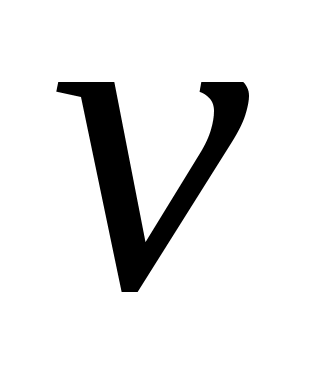 , найдется такое , найдется такое 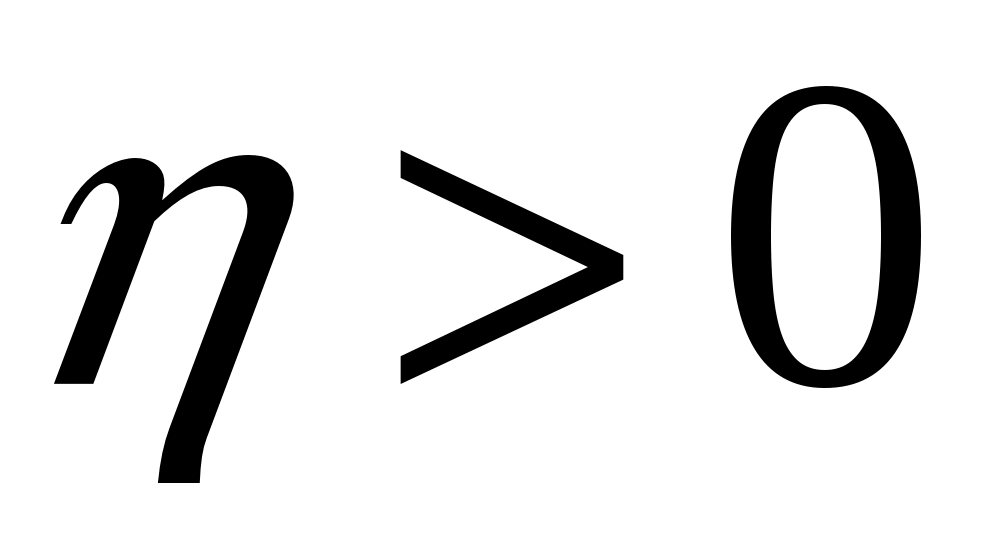 , что , что 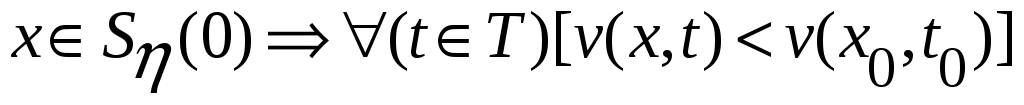 , а , а 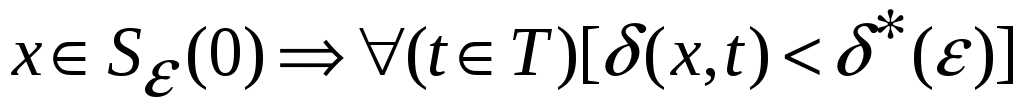 , с другой стороны, так как производная , с другой стороны, так как производная 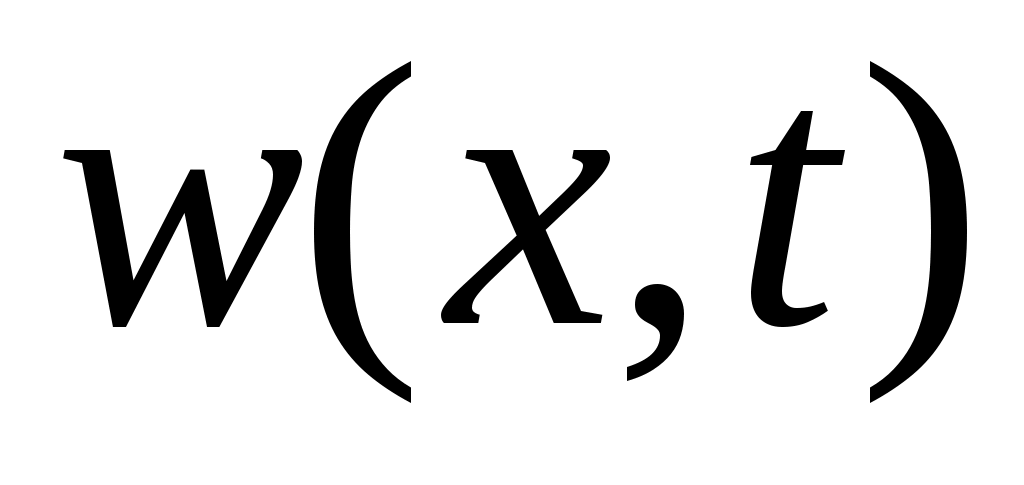 функции функции 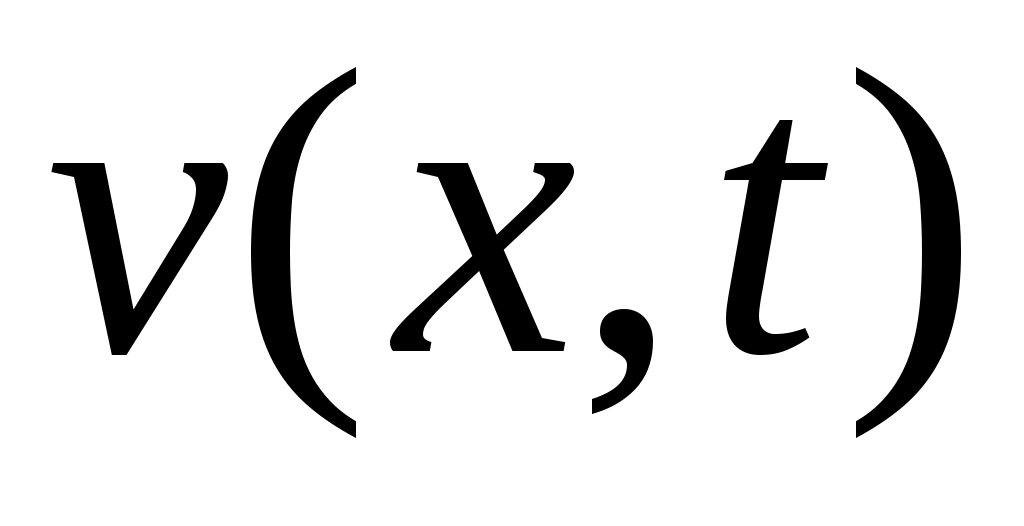 взятая вдоль траекторий системы, положительно определенная в окрестности взятая вдоль траекторий системы, положительно определенная в окрестности 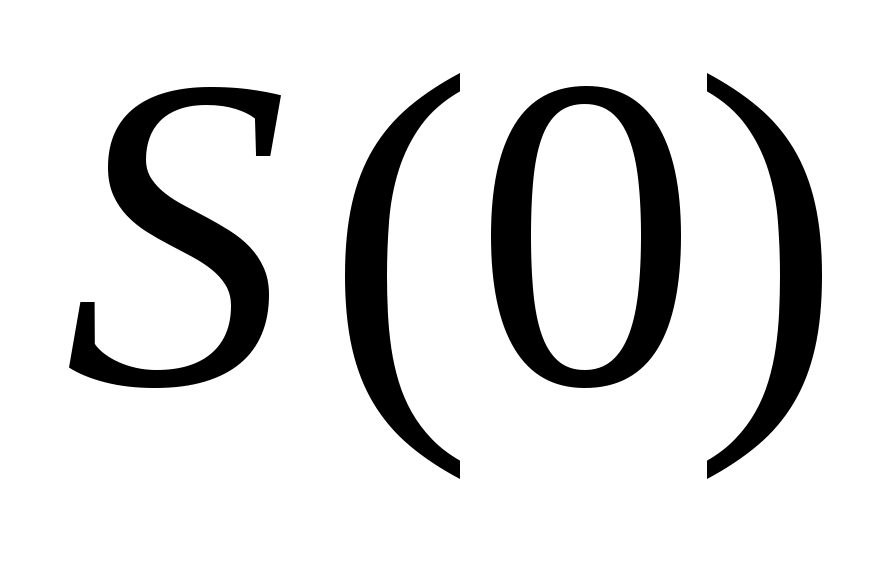 функция, то найдется такая знакоопределенная положительная функция функция, то найдется такая знакоопределенная положительная функция 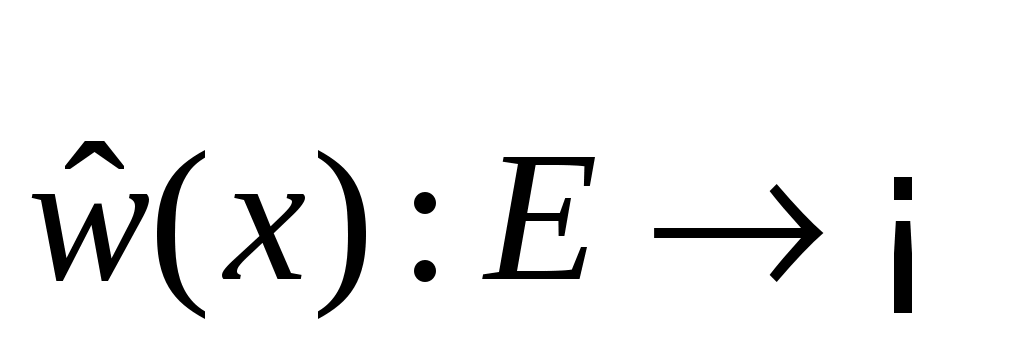 , что , что 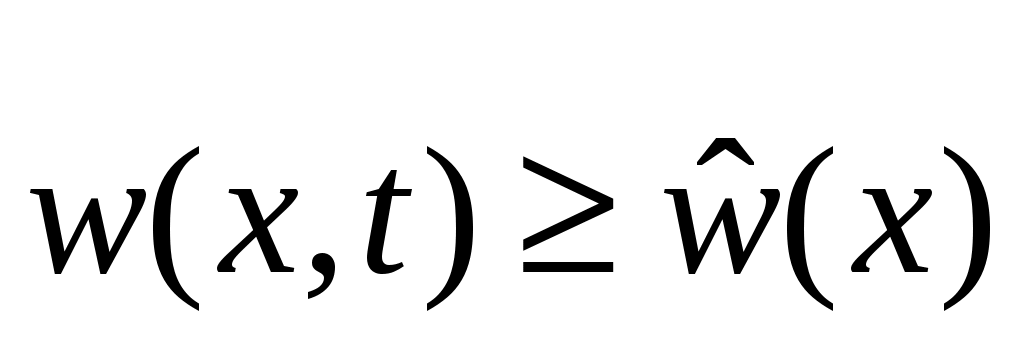 , а функция , а функция 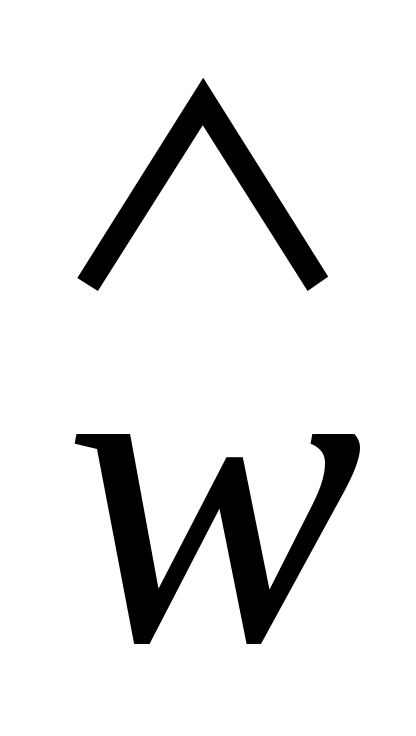 принимает на компакте принимает на компакте 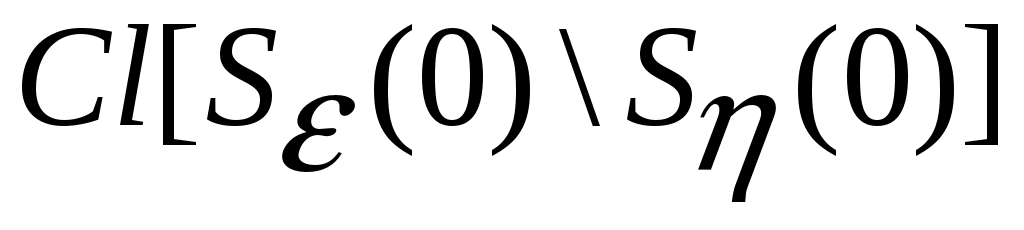 свое минимальное значение свое минимальное значение 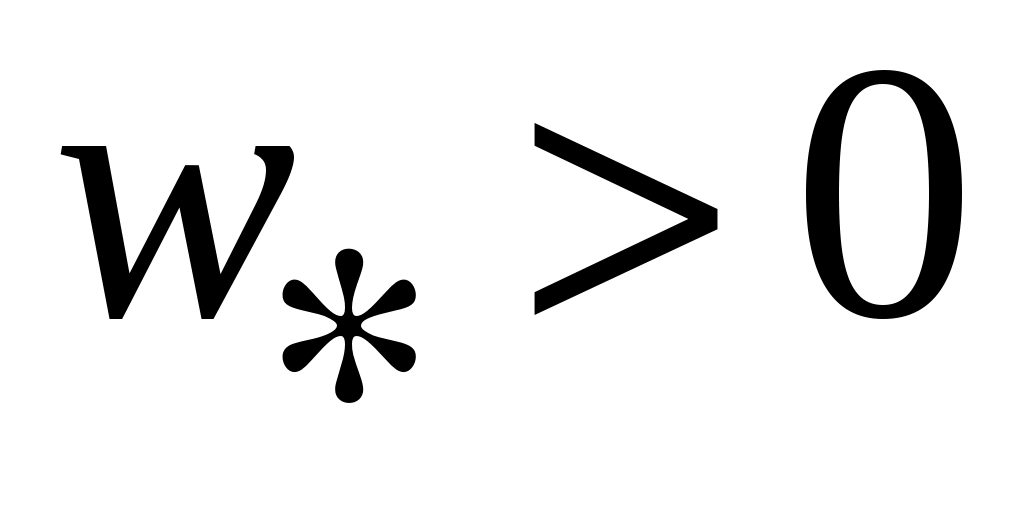 . Но тогда для величины функции . Но тогда для величины функции 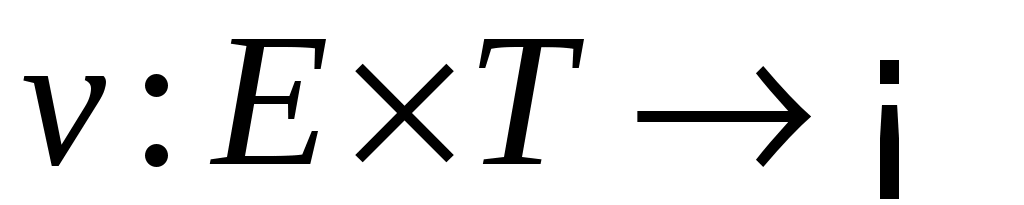 будут справедливы соотношения: будут справедливы соотношения: 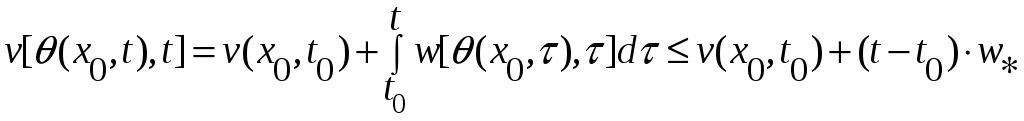 , и при достаточно больших , и при достаточно больших 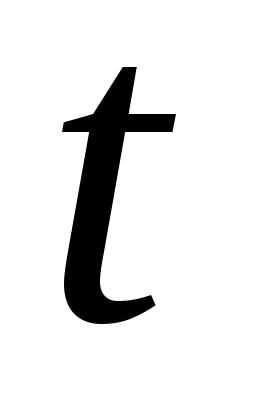 получим, что получим, что 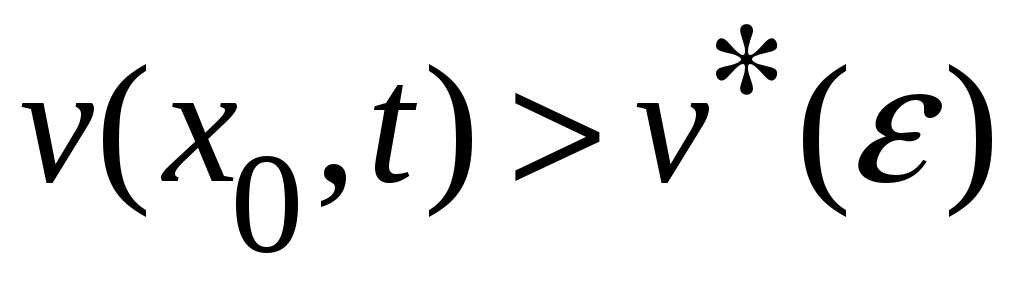 , что несовместимо с предположением , что несовместимо с предположением 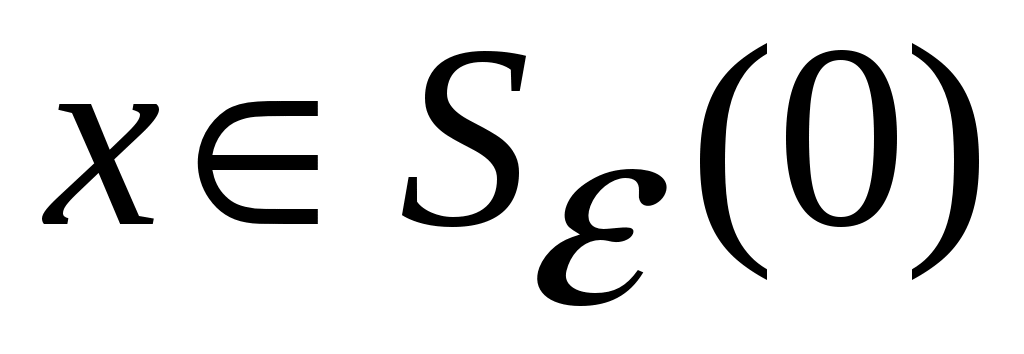 . .
При поиске функций Ляпунова могут быть полезны следующие замечания.
Для системы первого порядка, уравнение движения которой 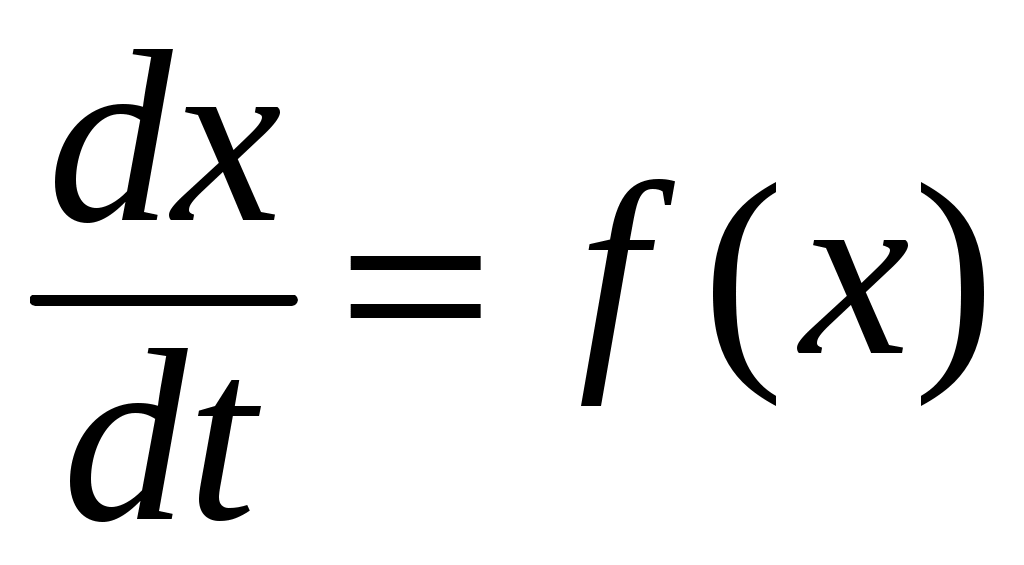 , где , где 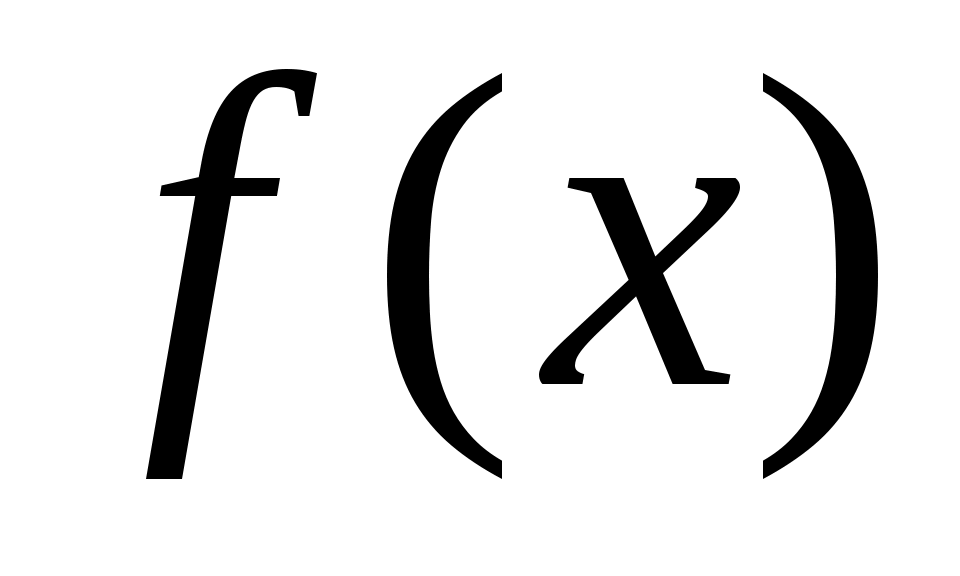 - непрерывная функция, такая, что - непрерывная функция, такая, что 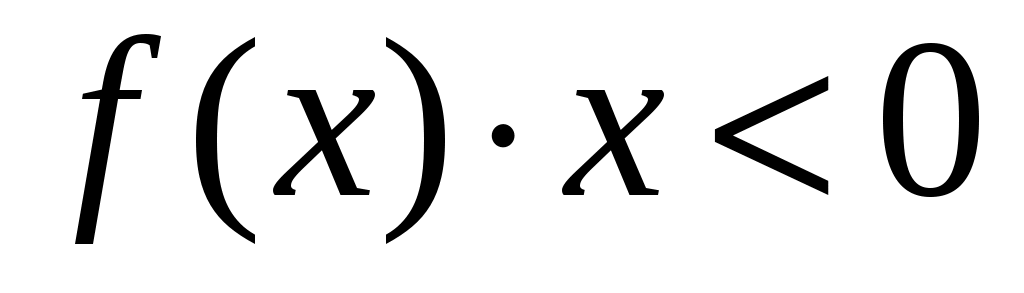 , всякая знакоопределенная положительная четная функция является функцией Ляпунова, сообщающей достаточные условия асимптотической устойчивости нулевого состояния равновесия. Если , всякая знакоопределенная положительная четная функция является функцией Ляпунова, сообщающей достаточные условия асимптотической устойчивости нулевого состояния равновесия. Если 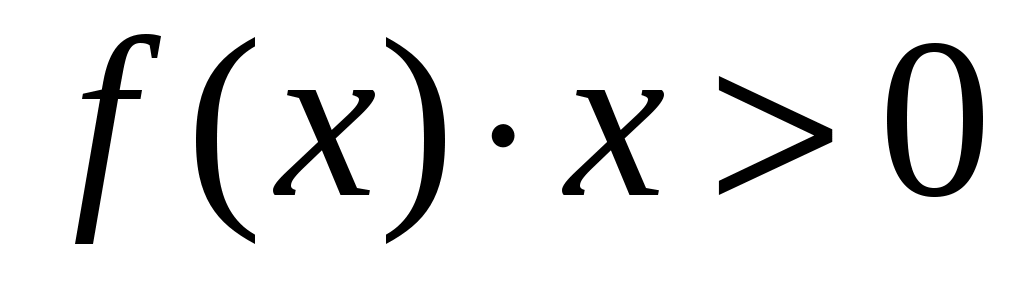 для всех для всех 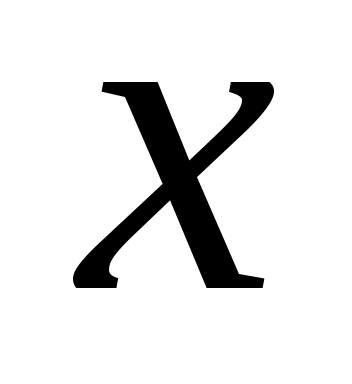 , то та же самая функция удовлетворяет достаточным условиям неустойчивости. , то та же самая функция удовлетворяет достаточным условиям неустойчивости.
Для системы 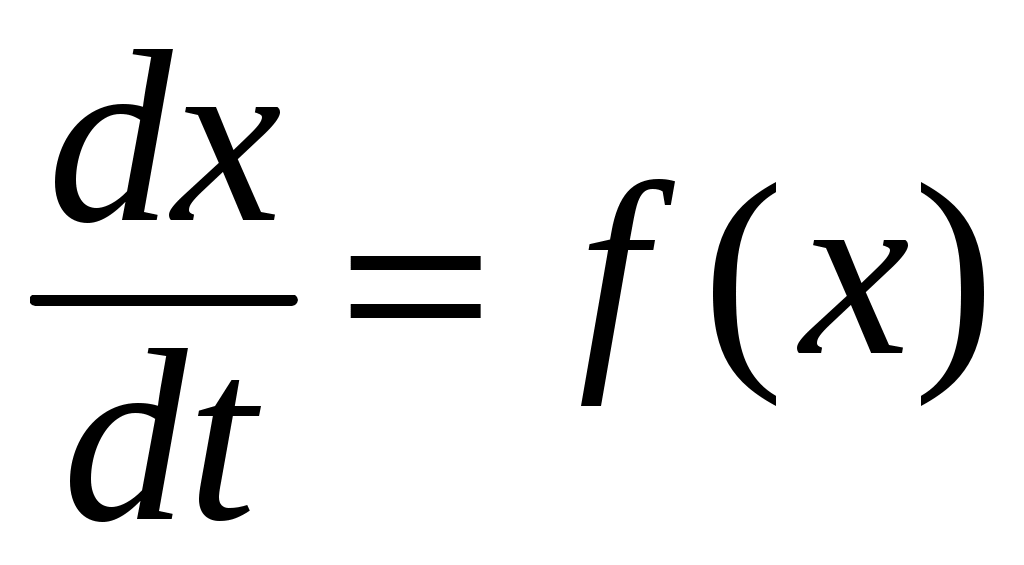 , где , где  , а , а 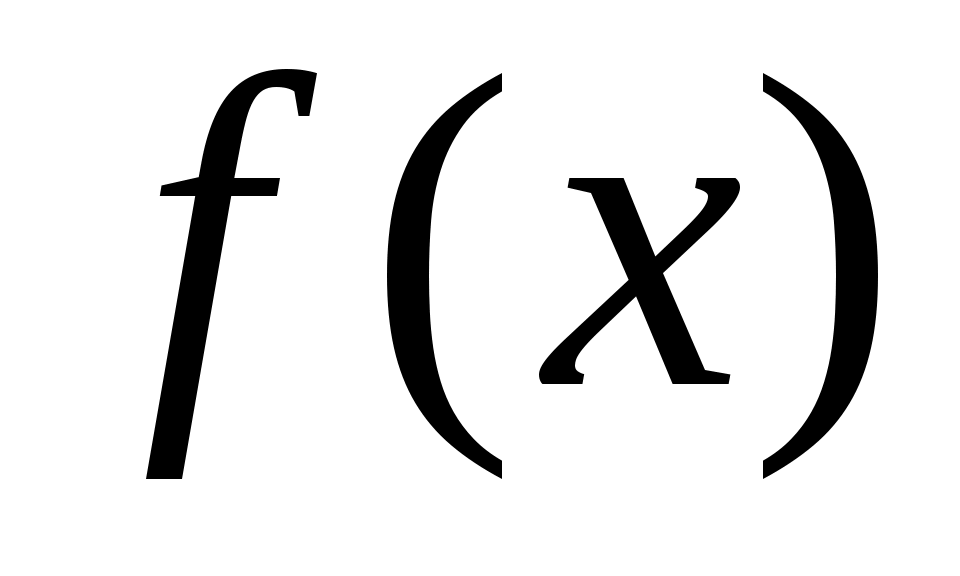 - четная положительно определенная функция, любая нечетная функция - четная положительно определенная функция, любая нечетная функция 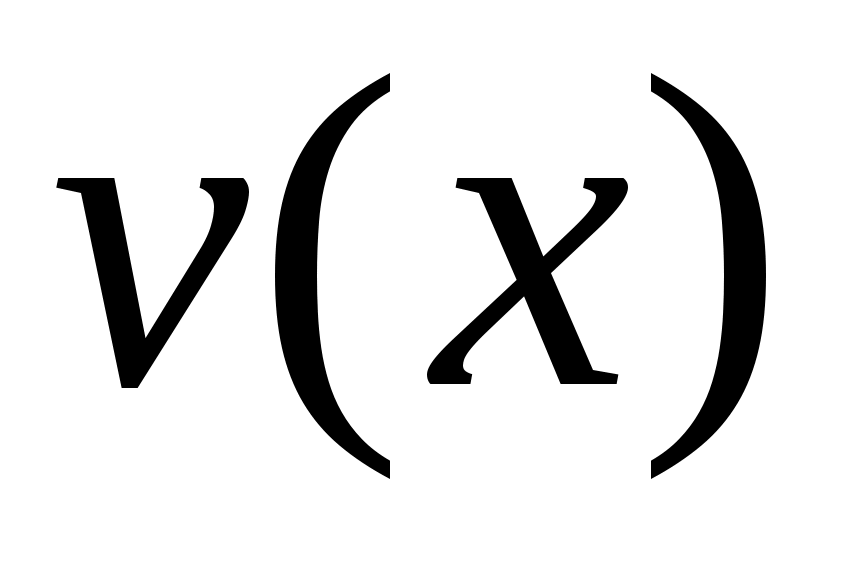 , такая, что , такая, что 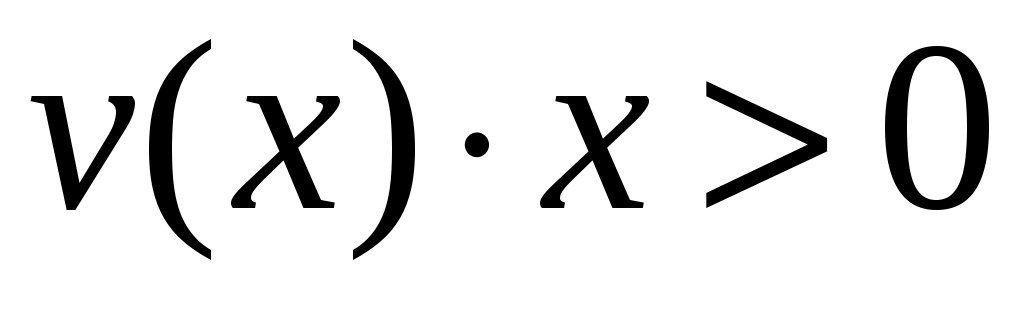 является функцией Ляпунова, удовлетворяющей условиям теоремы о неустойчивости. является функцией Ляпунова, удовлетворяющей условиям теоремы о неустойчивости. |
|
|
 Скачать 1.01 Mb.
Скачать 1.01 Mb.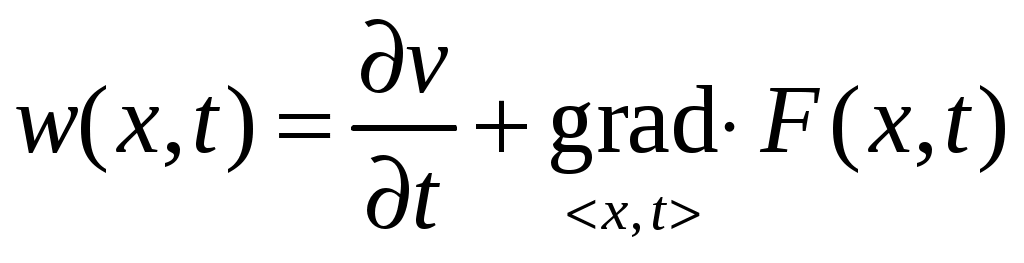 , (1)
, (1)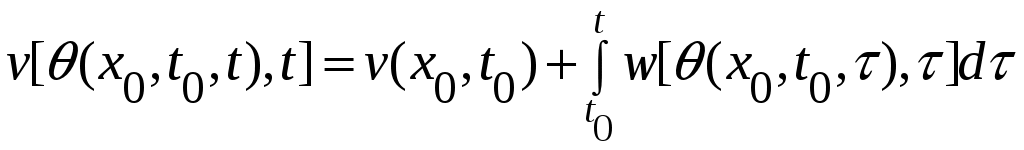 , (2)
, (2)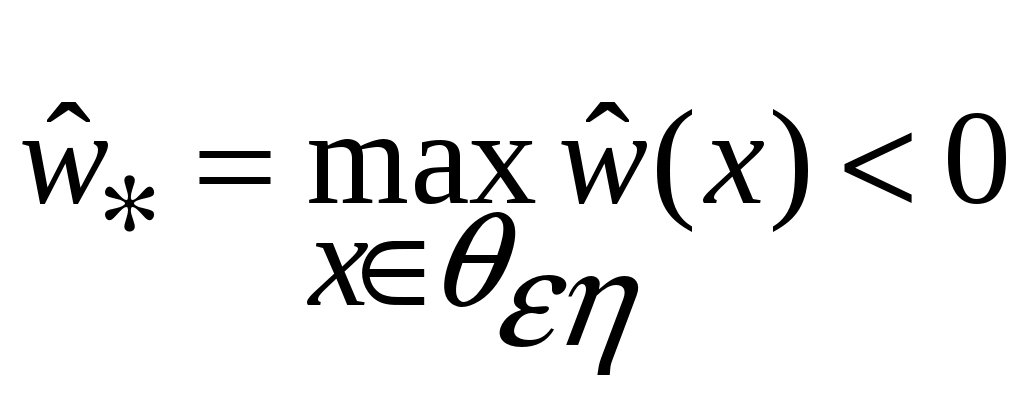 . При этом из (2) будет следовать на основании теоремы о среднем неравенство:
. При этом из (2) будет следовать на основании теоремы о среднем неравенство: 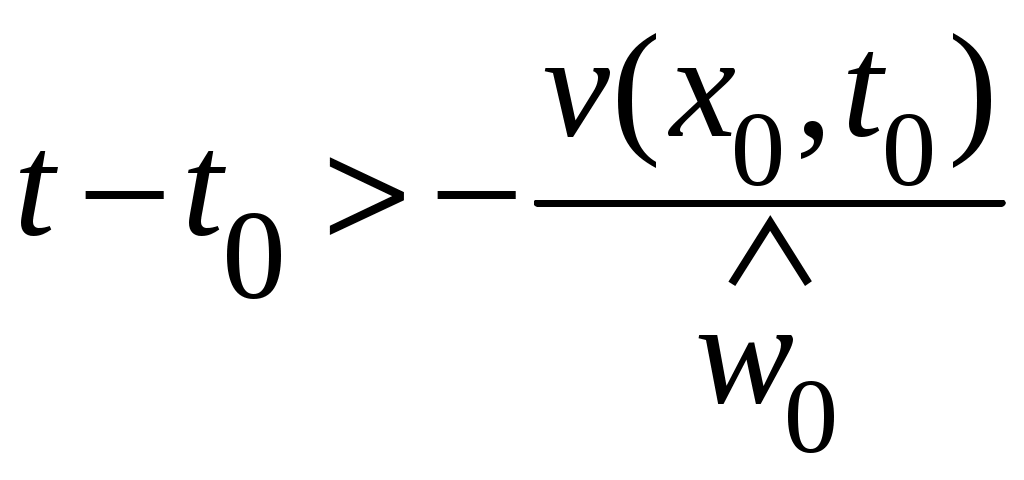 функция
функция 
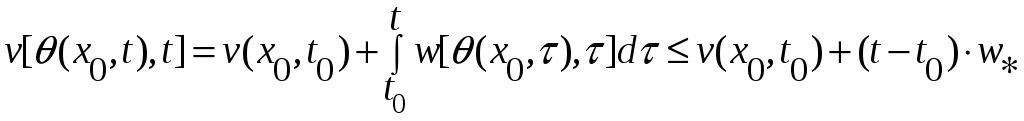 , и при достаточно больших
, и при достаточно больших 