прямоугольная изометрия. прямоугольная изометрическая проекция. Прямоугольная изометрическая проекция
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Прямоугольная изометрическая проекция Углы между осями х, у и z равны между собой, линейные размеры предмета, параллельные этим осям, искажаются одинаково (рис. 4.2). 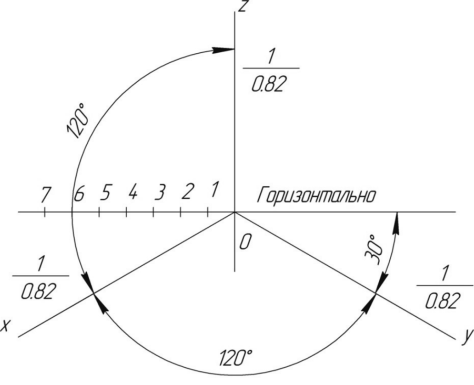 Рис. 4.2 При построении аксонометрии дробные показатели искажений усложняют расчет размеров. Для его упрощения пользуются приведенными показателями искажений: в изометрии все три показателя увеличивают в 1,22 раза (1:0,82«1,22), получая 1 (рис. 4.3). Так, длина всех ребер куба на изображении одинаковая, она равна 0,82 действительной длины. Для упрощения построений (как сказано выше) отрезки, параллельные аксонометрическим осям, откладываются действительной длины, без искажения. Известно, что любая линия или поверхность есть множество точек. Поэтому рассмотрение построения изометрической проекции рационально начать с построения точки. Точка А задана своими проекциями А, А2 и А3 (рис. 4.4) с координатами х, у, z. Построение изометрической проекции точки (рис. 4.5). Сначала строим оси, как показано на рис. 4.2. Откладывая от точки О (начала координат) последовательно отрезки на одной из осей и параллельные двум другим осям, равные величинам координат, мы всегда придем в точку А. Порядок построения координатной ломаной может быть любым из шести, представленных на рис. 4.5.  Рис. 4.3 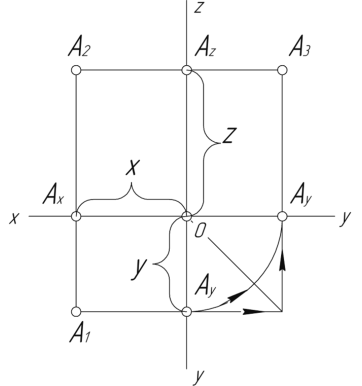 Рис. 4.4 Коэффициент искажения в изометрии К*0 = К^О = Kz0 =1:0,82« 1,22, принимаем равным единице (К*0 = К^О = Kz0 =1), поэтому координаты точки А на каждом примере (рис. 4.5) откладываем равными действительным координатам х,у, z (рис. 4.4).  Рис. 4.5 Линии штриховки сечений наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям («спроецированная» штриховка, рис. 4.6). Если основание тела правильный многоугольник (например, треугольник), то построенные прямоугольные изометрические проекции тела, ограниченного плоскостями, выполняют просто, а именно: построение вершин основания по координатам упрощается, если провести одну из осей координат через центр основания (рис. 4.7). 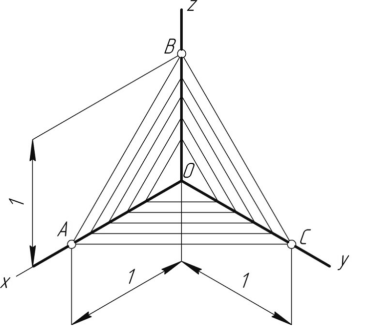 Рис. 4.6 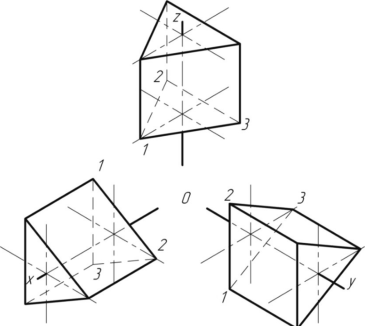 Рис. 4.7 Построив изометрию основания призмы, из вершин треугольника основания проводим прямые, параллельные соответственно осям х, у или z. На этих прямых от вершин основания отложим высоту призмы и получим изометрию вершин другого основания призмы. Соединив эти точки прямыми, получим изометрическую проекцию призмы. Прямоугольная изометрическая проекция окружности. Если построить изометрическую проекцию куба, в грани которого вписаны окружности диаметра D (рис. 4.8, а), то квадратные грани куба будут изображаться в виде ромбов, а окружности - в виде эллипсов (рис. 4.8, б). Малая ось C'D' каждого эллипса всегда должна быть перпендикулярна большой оси А В'. 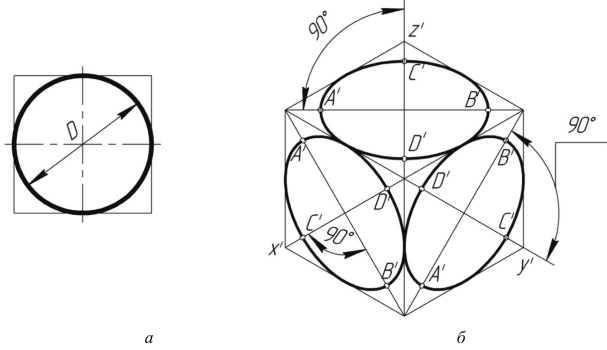 Рис. 4.8 Если окружность расположена в плоскости, параллельной горизонтальной плоскости, то большая ось А В' должна быть горизонтальной, а малая ось C'D' - вертикальной (рис. 4.8, б). Если окружность расположена в плоскости, параллельной фронтальной плоскости, то большая ось эллипса должна быть проведена под углом 90° к оси у'. При расположении окружности в плоскости, параллельной профильной плоскости, большая ось эллипса будут проходить под углом 90° к осих'. Большие оси эллипсов всегда перпендикулярны соответствующим осям, а малые - им параллельны. При построении изометрической проекции окружности без сокращения по осям х у' и z' длина большой оси эллипса берется равной 1,22 диаметра D изображаемой окружности, а длина малой оси эллипса - 0,7 ID (рис. 4.9). 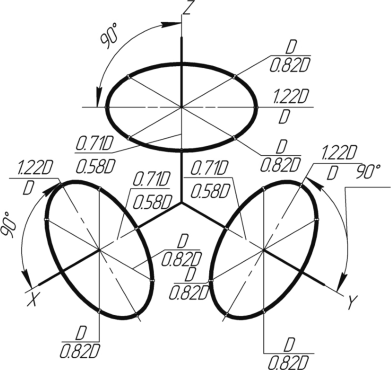 Рис. 4.9 На рис. 4.10, 4.12 и 4.14 показаны поверхности вращения, выполненные в изометрии с овалами, расположенными параллельно горизонтальной плоскости проекций (рис. 4.10), фронтальной плоскости проекций (рис. 4.12), профильной плоскости проекций (рис. 4.14). В учебных чертежах для упрощения построения изометрических проекций окружности вместо эллипсов рекомендуется применять овалы, очерченные дугами окружностей. Упрощенный способ построения изометрических овалов приведен на рис. 4.11,4.13, 4.15. Для построения овала в плоскости, параллельной горизонтальной плоскости проекций (рис. 4.11), проводим оси х и у (рис. 4.2), соответствующие вертикальной и горизонтальной осям плоскости. Из точки пересечения осей О проводим вспомогательную окружность диаметром D, равным действительной величине диаметра изображаемой окружности, и находим точки N - точки пересечения этой окружности с аксонометрическими осями х и у. Из точек М пересечения вспомогательной окружности с осью z как из центров радиусом R = NM проводим две дуги - NDN и NCN окружности, принадлежащие овалу.  Рис. 4.10  Рис. 4.11  Рис. 4.12 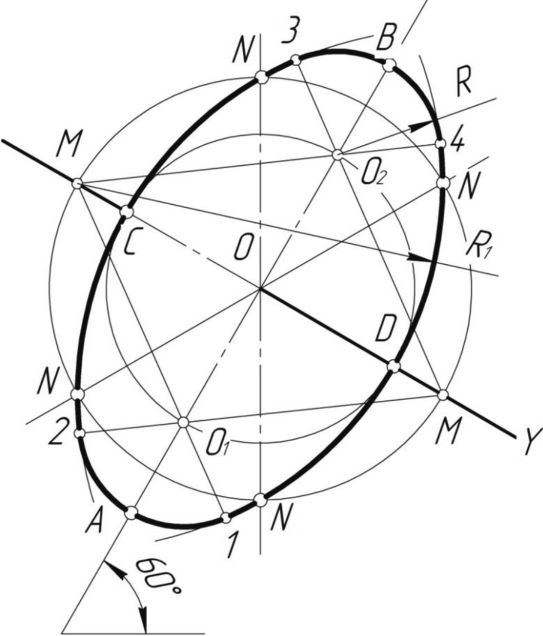 Рис. 4.13  Рис. 4.14  Рис. 4.15 Из центра О радиусом ОС, равным половине малой оси овала, строим окружность и находим на большой оси овала АВ точки 0. Из этих точек радиусом R = 0 = 0(1 = 03 = О4 проводим две дуги. Точки 7, 2, 3 и 4 сопряжений дуг радиусов R и R] находим, соединяя точки М с точками 0 и продолжая прямые до пересечения с дугами NCNnNDN. На рис. 4.13 показано упрощенное построение изометрической проекции окружности, расположенной в плоскости, параллельной фронтальной плоскости проекций. Построение аналогично построению изометрического овала окружности, расположенной в плоскости, параллельной горизонтальной плоскости проекций, разница лишь в том, что большую ось овала АВ располагают перпендикулярно малой оси CD, принадлежащей оси у. На рис. 4.15 показано упрощенное построение изометрической проекции окружности, расположенной в плоскости, параллельной профильной плоскости проекций. Построение аналогично построению изометрического овала окружности, расположенной в плоскости, параллельной профильной плоскости проекций, разница лишь в том, что большую ось овала АВ располагают перпендикулярно малой оси CD, принадлежащей оси х. На рис. 4.16 приведен пример построения овалов на изометрии детали с расположением окружностей в плоскостях, параллельных горизонтальной, фронтальной и профильной плоскостям проекций. 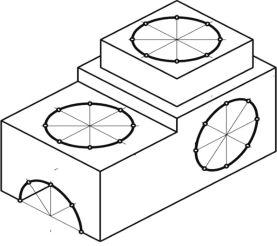 Рис. 4.16 Построение аксонометрической проекции детали следует начинать с изображения на чертеже аксонометрических осей. Целесообразно за начало координат принимать центр симметрии, а за оси координат - оси симметрии детали. При построении аксонометрии рекомендуется мысленно разделить деталь на простейшие геометрические тела (цилиндр, конус, призма, пирамида и т. и.). После изображения аксонометрических проекций составных элементов предмета строятся конструктивные скругления в местах их соединения. Линии, изображающие проекции ребер предмета, параллельны одноименным аксонометрическим осям, поэтому при построении аксонометрических проекций удобно использовать прямые, параллельные аксонометрическим осям. Как и на комплексном чертеже, полые детали в аксонометрии рекомендуется выполнять с разрезом (вырезом части) (рис. 4.17). 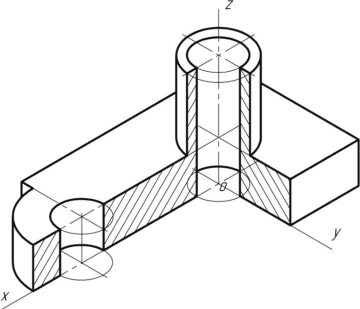 Рис. 4.17 Если окружность неполная, то для ее изображения вычерчивают тонкой линией полный овал или эллипс, а затем обводят нужную часть овала (рис. 4.17). Как начертить изометрию? Практически все, кому довелось изучать черчение и инженерную графику сталкивались с необходимостью произвести построение изометрической проекции детали. Разбирем основные моменты, которые нужно знать, чтоб начертить изометрию. В вашей детали может быть большее количество построений, но основные принципы останутся неизменными. Но построение изометрии скорее всего будет вам не под силу, если вы еще не освоили построение третьего вида и построение простого разреза. Вы должны уже уметь хорошо ориентироваться в трех видах на чертеже. Начнем с того, что определимся с направлением осей в изометрии. 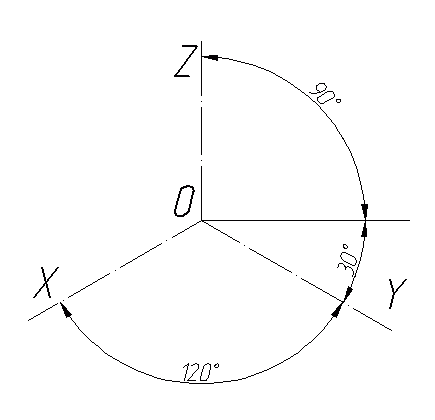 На следующей схеме показано соответствие направлений, по которым откладываются размеры в изометрии по отношению к размерам на чертеже. 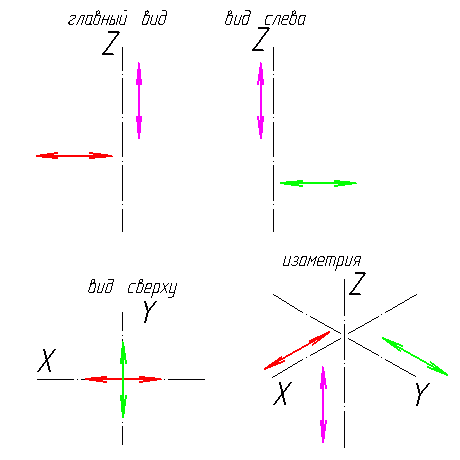 Возьмем для примера не очень сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм. 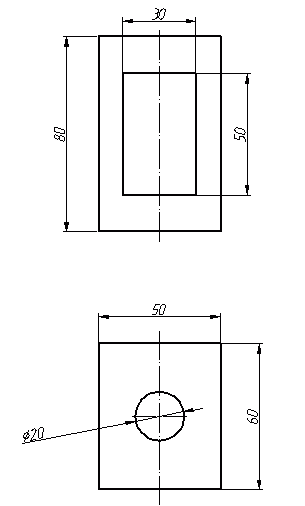 Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок параллельный оси У длиной 60 мм. Отложим по оси У 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру. 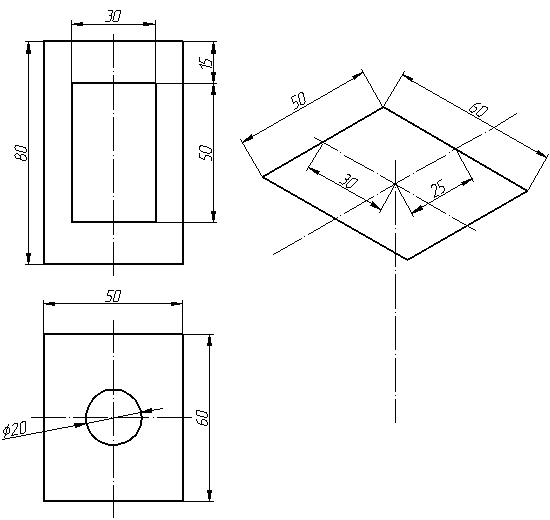 Мы получили верхнюю грань фигуры. Не хватает только отверстия диаметром 20 мм. Построим это отверстие. В изометрии окружность изображается особым образом - в виде эллипса. Это связано с тем, что мы смотрим на нее под углом. В изометрии окружности проецируются в эллипсы с размерами осей a=1,22D и b=0,71D. Эллипсы, обозначающие окружности на горизонтальных плоскостях в изометрии изображаются с осью а расположенной горизонтально, а ось b - вертикально. При этом расстояние между точками расположенными на оси Х или У равно диаметру окружности (смотри размер 20 мм). 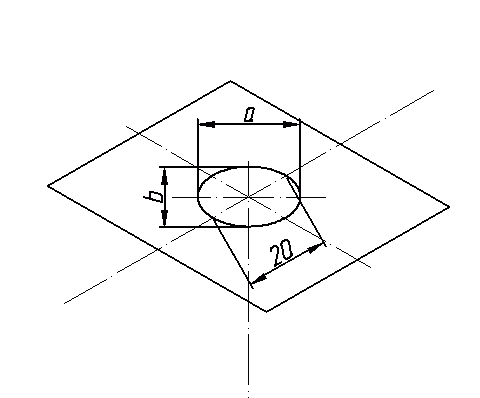 Теперь, из трех углов нашей верхней грани начертим вниз вертикальные ребра - по 80 мм и соединим их в нижних точках. Фигура почти полностью начерчена - не хватает только прямоугольного сквозного отверстия. 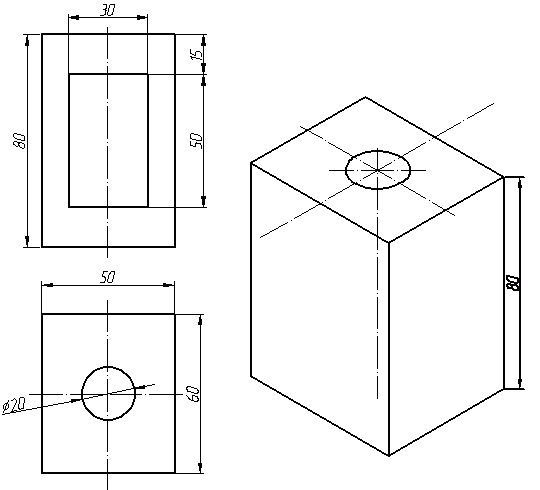 Чтобы начертить его опустим вспомогательный отрезок 15 мм из центра ребра верхней грани (указан голубым цветом). Через полученную точку проводим отрезок 30 мм параллельный верхней грани (и оси Х). Из крайних точек чертим вертикальные ребра отверстия - по 50 мм. Замыкаем снизу и проводим внутреннее ребро отверстия, оно параллельно оси У. 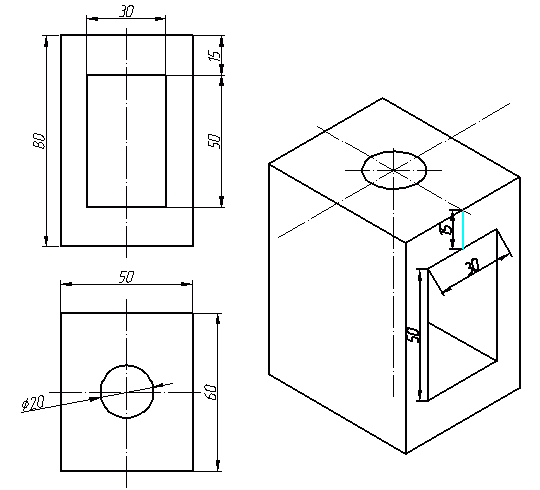 На этом простая изометрическая проекция может считаться завершенной. Но как правило, в курсе инженерной графики выполняется изометрия с вырезом одной четверти. Чаще всего, это четверть нижняя левая на виде сверху - в этом случае получается наиболее интересный с точки зрения наблюдателя разрез (конечно же все зависит от изначальной правильности компоновки чертежа, но чаще всего это так). На нашем примере эта четверть обозначена красными линиями. Удалим ее.  Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили). 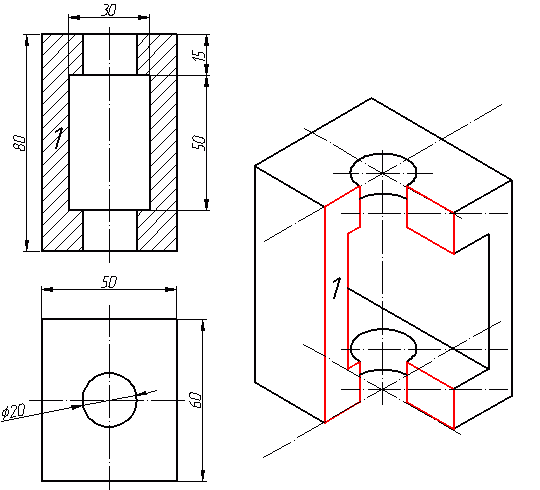 |
