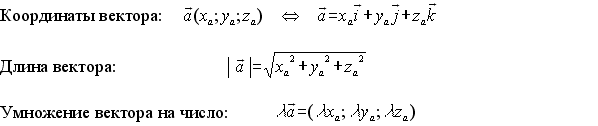|
|
Лекция. Прямоугольная система координат. Векторы в пространстве. Координаты вектора. Прямоугольная система координат. Векторы в пространстве. Координаты вектора
Прямоугольная система координат. Векторы в пространстве. Координаты вектора.
Прямоугольная система координат.
Векторы в пространстве. Координаты вектора
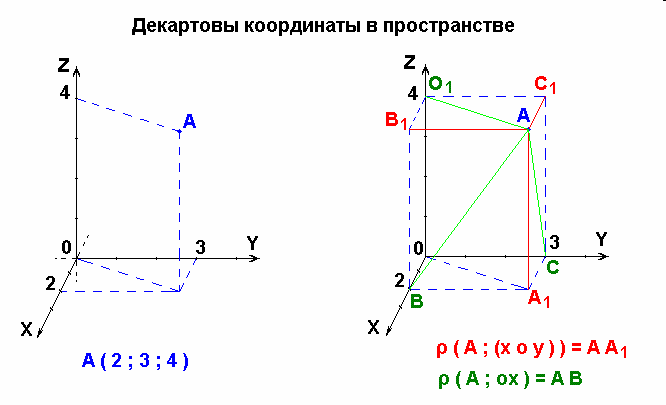
Прямые x, y, z называются координатными осями (или осями координат),
точка их пересечения O – началом координат,
а плоскости xOy, xOz и yOz – координатными плоскостям.Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями.
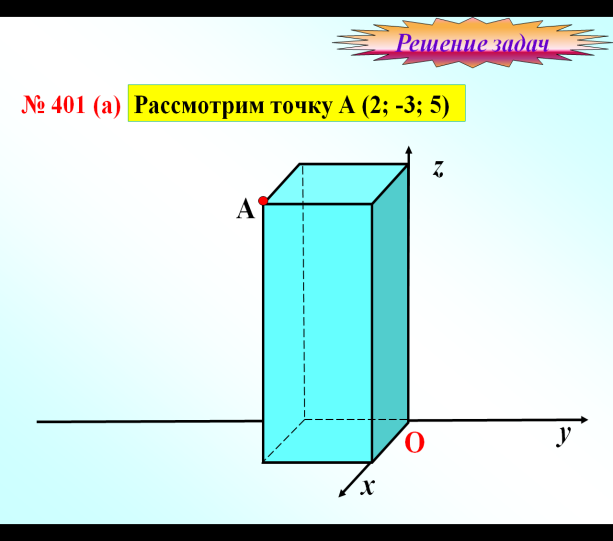
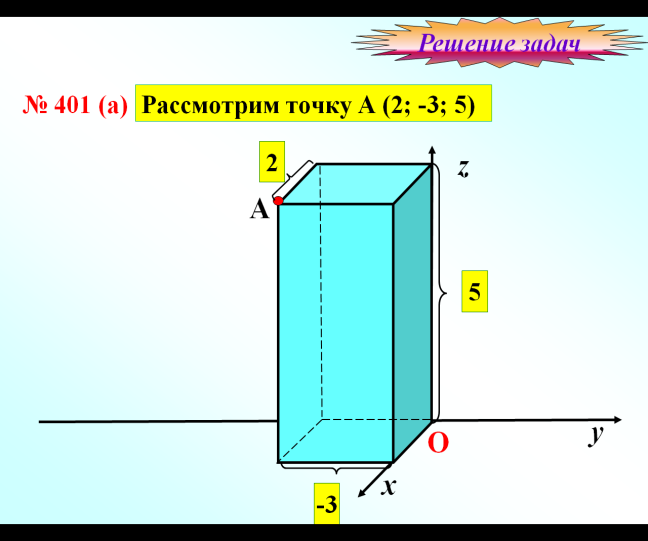
Определение. Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OAx: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси. Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).
|
|
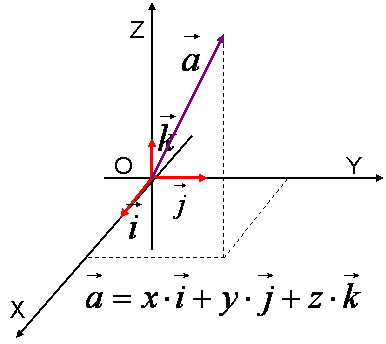
Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси.
Вектора i , j , j , k , k называются координатными векторами. Любой вектор можно разложить по координатным векторам: называются координатными векторами. Любой вектор можно разложить по координатным векторам: 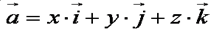 Коэффициенты разложения определяются единственным образом и называются координатами вектора Коэффициенты разложения определяются единственным образом и называются координатами вектора 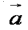 в данной системе координат. в данной системе координат.
Единичный вектор, направленный вдоль оси x, обозначается i . .
Единичный вектор, направленный вдоль оси y, обозначается j . .
Единичный вектор, направленный вдоль оси z, обозначается k . .
|
|
Координаты нулевого вектора равны нулю.
Координаты равных векторов соответственно равны.
Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов.
Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов.
Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число. 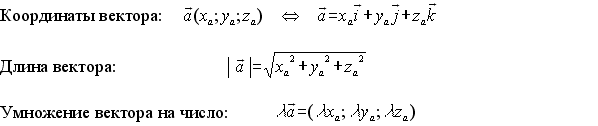
Задание
Пример
Задание. Найти длину вектора 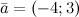
Решение. Используя формулу, получаем:
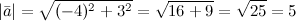
Пример
Задание. Найти длину вектора 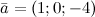
Решение. Используя формулу, получаем:
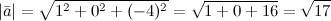
Пример
Запись 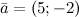 означает, что вектор означает, что вектор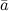 имеет следующие координаты: абсцисса равна 5, ордината равна -2. имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Пример
Задание. Заданы векторы 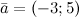 и и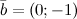 . Найти координаты вектора . Найти координаты вектора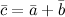
Решение. 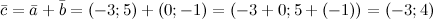
Пример
Задание. Вектор 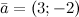 . Найти координаты вектора . Найти координаты вектора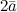
Решение. 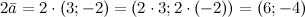
|
| |
|
|
 Скачать 192.5 Kb.
Скачать 192.5 Kb.