Задачи цилиндр. R12r2 h23h1

• Название: R12r2 h23h1
• Дата: 23.03.2022
• Размер: 0.91 Mb.
• Имя файла: Задачи цилиндр.rtf
• Тип: Документы; #411027

1. 
   Два прямых круговых цилиндра C1 и C2 известно, что у C1 радиус основания в два раза больше, чем у C2, но у C2 высота в три раза больше, чем у C1. Найдите отношение объёма цилиндра C2 к объёму C1.
   
   Обозначим высоту цилиндра C1 через h1, а высоту цилиндра C2 через h2. Обозначим радиус основания цилиндра C1 через r1, а радиус основания цилиндра C2 через r2. Тогда
   r1=2*r2 h2=3*h1
   Объём цилиндра C1 равен πr12h1=4πr22h1, а объём цилиндра C2 равен объём цилиндра C2 равен 3πr22h1, тогда
   
   тогда VC2/VC1=3πr2²h1/4πr2²h1=0,75
   

Ответ: 0,75

2. 
   Объем цилиндра равен 64π, а площадь боковой поверхности равна 32π. Найдите площадь полной поверхности цилиндра, деленную на π.
   
   

Формулы для нахождения объема и боковой поверхности цилиндра: V=πR2h, б о к Sбок=2πRh. Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: б о к V/Sбок=πR²h/2πRh=R2=64π/32π=2 ⇒ R=4. Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований: п о л н Sполн=2πRh+2πR2=32π+2⋅16π=64π. Осталось разделить полученный объем на π, тогда окончательно получаем 64. Ответ: 64

3. 
   Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на π.
   Площадь боковой поверхности цилиндра вычисляется по формуле Sбок=2πRh где h – высота цилиндра,  R– радиус.
   

Тогда Sбок= 2п*7*10=140п

Следовательно,  140п/п=140

Ответ: 140.  

4. 
   Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
   
   
5. 
   В цилиндрический сосуд налили 1200 см³  воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? Ответ выразите в см³.
   

Vцилиндра = πr²h
1 мл=1см³
Sоснования =1200:12=100 (см²)
По закону Архимеда объем детали будет равен объёму "вытесненной" жидкости. Найдём объём жидкости.
V=S×h=100×10=1000 (см³)

6. 
   Даны две круж­ки ци­лин­дри­че­ской формы. Пер­вая круж­ка в пол­то­ра раза ниже второй, а вто­рая вдвое шире первой. Во сколь­ко раз объём вто­рой круж­ки боль­ше объёма первой?
   

V1=π*r²*h
V2=π*(2r)²*(1.5h)=π*4*r²*1.5h=6π*r²*h
V2/V1=6π*r²*h/(π*r²*h)=6 раз

7. 
   Радиус ос­но­ва­ния цилиндра равен 26, а его об­ра­зу­ю­щая равна 9. Сечение, па­рал­лель­ное оси цилиндра, уда­ле­но от неё на расстояние, рав­ное 24. Най­ди­те площадь этого сечения.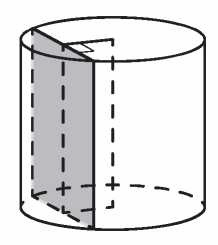
   

Из прямоугольного треугольника OHA, AH=OA²−OH²​=29²−20²​=21, следовательно, AB=2AH=2 * 21=42, AB=2AH=2⋅21=42. Учитывая, что по условию AC=50, получаем площадь сечения S=50⋅42=2100.