Рабочая тетрадь 1. Рабочая тетрадь 1
 Скачать 371.64 Kb. Скачать 371.64 Kb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| «Информатика – это наука о методах и процессах сбора, хранения, обработки, передачи, анализа и оценки информации с применением компьютерных технологий, обеспечивающих возможность ее использования для принятия решений». Большая российская энциклопедия, 2008. |
| «Информация – это сведения, независимо от формы их представления, воспринимаемые человеком или специальными устройствами как отражение фактов материального мира в процессе коммуникации». ГОСТ 7.0-99. |
| 1. Теоретический материал | |
| Бит – это минимальная единица измерения информации. Бит может принимать только два значения 0 или 1 [1, 2]. В вычислительных системах приняты следующие единицы измерения представления цифровых данных: 8 бит = 1 байт (1 Б), 1024 байт (1024 Б ) = 1 килобайт (1 Кбайт), 1024 килобайт (1024 Кбайт) = 1 мегабайт (1 Мбайт), 1024 мегабайт (1024 Мбайт) = 1 гигабайт (1 Гбайт), 1024 гигабайт (1024 Гбайт) = 1 терабайт (1 Тбайт). | |
| 2. Пример | |
| Задача: | |
| | Сколько битов в 3 Мбайт? |
| Решение: | |
| | 3 Мбайт = 3 * 1024 Кбайт = 3* 1024 * 1024 Б = = 3* 1024 * 1024 * 8 бит = 25165824 бит |
| Ответ: | |
| | 25165824 бит |
| 3. Задания | ||
| 1. | Задача: | |
| | Сколько битов в 4 Мбайт? | |
| Решение: | ||
| | 4 Мб = 4 * 1024 Кб = 4 * 1024 * 1024 * 8 бит = 33 554 432 бит | |
| Ответ: | ||
| | 33 554 432 бит | |
| 2. | Задача: | |
| | Сколько байтов в 2 Гбайт? | |
| Решение: | ||
| | 2 Гб = 1024 * 1024 * 1024 * 2 байт = 214 484 000 байт | |
| Ответ: | ||
| | 214 484 000 байт | |
| 3. | Задача: | |
| | Переведите 6291456 байт в Мбайт? | |
| Решение: | ||
| | 6 291 456 / (1024 * 1024) = 6 | |
| Ответ: | ||
| | 6 Мб | |
| 1. Теоретический материал |
| Формула N = log2K, где K – количество возможных состояний, а N – минимальное количество информации в битах, необходимое для описания состояний системы – формула Хартли [1, 2]. При вычислении по формуле Хартли может получено нецелое значение N. В этом случае значение необходимо округлить вверх до целого значения. |
| 2. Пример | |||
| 1. | Задача: | ||
| |
| ||
| Решение: | |||
| | Если не различать буквы Е и Ё, то в русском алфавите 32 буквы. Тогда: log232= 5 . Получилось целое число. | ||
| Ответ: | |||
| | 5 бит | ||
| 2. | Задача: | ||
| | Сколько бит нужно отвести на кодирование букв русского алфавита, если различать буквы Е и Ё? | ||
| Решение: | |||
| | Если различать буквы Е и Ё, то в русском алфавите 33 буквы. Тогда: log233 = 5,044 . Получилось не целое число. Поэтому округлим в верхнюю сторону до 6. | ||
| Ответ: | |||
| | 6 бит | ||
| 3. Задания | |||
| 1. | Задача: | ||
| |
| ||
| | Решение: | |
| | Log(2)26 5 | |
| Ответ: | ||
| | 5 бит | |
| 2. | Задача: | |
| | Сколько бит нужно отвести на кодирование гласных букв английского алфавита? | |
| Решение: | ||
| | Log(2)5 3 | |
| Ответ: | ||
| | 3 Бита | |
| 3. | Задача: | |
| | Сколько бит нужно отвести на кодирование согласных букв английского алфавита? | |
| Решение: | ||
| | Log(2)21 5 | |
| Ответ: | ||
| | 5 bit | |
| 1. Теоретический материал | |
| Пусть теперь система может находиться в одном из K состояний с разными вероятностями [1]. В состоянии 1 с вероятностью 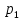 , в состоянии 2 с вероятностью , в состоянии 2 с вероятностью 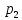 и продолжая рассуждения в состоянии K с вероятностью и продолжая рассуждения в состоянии K с вероятностью 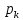 , где , где 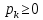 . Тогда ценность знания, что система находится в состоянии . Тогда ценность знания, что система находится в состоянии 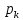 зависит от распределения вероятностей [1]. зависит от распределения вероятностей [1].Фундаментальное понятие теории информации – энтропия информации. Под энтропией понимается мера неопределенности системы. Энтропией по Шеннону называется число 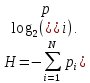 Прирост информации – это уменьшение энтропии. | |
| 2. Пример | |
| Задача: | |
| | Если двоечник не поступил в РТУ МИРЭА, то тут мало информации, потому что «мы это и так знали», а вот если он поступил, то это «новость»! Полагая, что двоечник не поступает с вероятностью 0,9, а поступает с вероятностью 0,1, найдите энтропию по Шеннону [1]. |
| Решение: | |
| | Частная энтропия для не поступления равна: -0,9 * log20,9 = 0,137, а для поступления равна: -0,1 * log20,1 = 0,332. А общая энтропия равна: H = 0,137 + 0,332 = 0,469. |
| Ответ: | |
| | H = 0,469. |
| 3. Задания | ||
| 1. | Задача: | |
| | Найти энтропию подбрасывания одной монеты. | |
| Решение: | ||
| | -0,5 * log(2)0,5 = 0,5 | |
| | Ответ: | |
| | 0,5 | |
| 2. | Задача: | |
| | Найти энтропию подбрасывания игральной кости. | |
| Решение: | ||
| | -(1/6)*log(2)(1/6) = 0,43 | |
| Ответ: | ||
| | 0,43 | |
| 3. | Задача: | |
| | Имеется очень загруженный сервер. Из-за этого с вероятностью 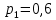 сервер принимает запрос на обработку данных и с вероятностью сервер принимает запрос на обработку данных и с вероятностью 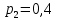 отвергает его. Найти частные энтропии и общую энтропию системы. отвергает его. Найти частные энтропии и общую энтропию системы. | |
| Решение: | ||
| | Частные 0,53-0,44 = 0,09 Общая 0,97 | |
| Ответ: | ||
| | | |


