1. Теоретический материал
|
Кодирование – это процесс преобразования данных в цифровой формат для хранения, передачи и обработки в вычислительных системах.
Вся цифровая информация в вычислительных системах представляется в двоичном коде – наборе нулей и единиц. Двоичный код – это кодирование каждого объекта последовательностью бит.
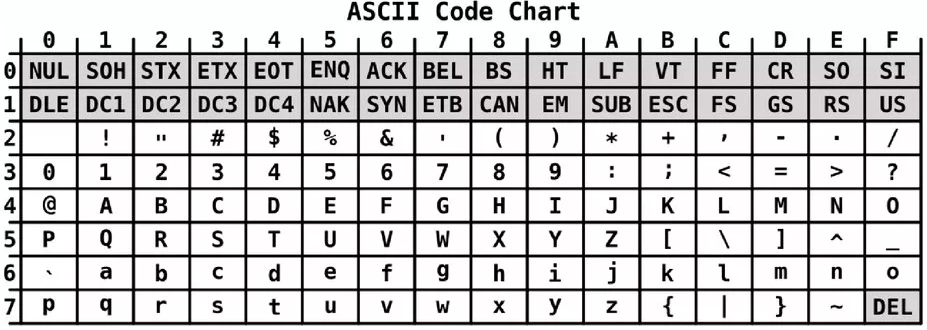
На рисунке представлена таблица ASCII кодов символов английского алфавита с учетом прописных букв, знаков препинания, чисел, арифметических операций и некоторых других вспомогательных символов.
Таблица ASCII однозначно определяет 128 символов, расширенная ASCII таблица содержит 256 символов (1 байт) и включает русский алфавит.
При кодировании символов всех алфавитов (японского, китайского и других) одного байта недостаточно, поэтому применяется Unicode, который измеряется двумя байтами – количество символов 216 = 65536.
|
2. Пример
|
Задача:
|
|
Найти ASCII код символа N
|
Решение:
|
|
Символ N находится на пересечении строки 4 и столбца E, поэтому он кодируется 4E16 в шестнадцатеричной системе счисления.
|
Ответ:
|
|
4E16
|
3. Задания
|
1.
|
Задача:
|
|
Найти ASCII код символа w(строчная буква).
|
Решение:
|
|
|
Ответ:
|
|
7716
|
2.
|
Задача:
|
|
Найти символ по ASCII коду 7516.
|
Решение:
|
|
|
Ответ:
|
|
u
|
3.
|
Задача:
|
|
Запишите слово student набором символов ASCII кода.
|
Решение:
|
|
s = 7316
t = 7416
u = 7516
d = 6416
e = 6516
n = 6E16
t = 7416
|
Ответ:
|
|
7316 7416 7516 6416 6516 6E16 7416
|
1. Теоретический материал
|
Важная задача кодирования – это возможность обнаружения ошибок, которые возникают в процессе хранения и/или передачи информации [1].
Рассмотрим простейший способ обнаружения однократной ошибки – бит четности. Например, байт представлен восьмью битами. Тогда в пересылаемом сообщении добавляется девятый бит – бит четности, который равен единице, если количество бит в исходном байте нечетно и нулю, если количество бит четно.
Исходное сообщение
|
Пересылаемое сообщение
|
Полученное сообщение
|
Проверка
|
01101101
|
011011011
|
011011011
|
Ок. Чётное число единиц
|
01010101
|
010101010
|
010101010
|
Ок. Чётное число единиц
|
01011101
|
010111011
|
010011011
|
Ошибка. Нечётное число единиц
|
01011101
|
010111011
|
010111010
|
Ошибка. Нечётное число единиц
|
|
2. Пример
|
Задача:
|
|
Добавьте бит чётности к следующему сообщению: 01101011 .
|
Решение:
|
|
В сообщении не четное число бит, поэтому в конце к нему нужно дописать единицу, чтобы пересылаемое сообщение содержало чётное число единиц, т.е. 011010111
|
Ответ:
|
|
011010111
|
3. Задания
|
1.
|
Задача:
|
|
Добавьте бит чётности к следующему сообщению: 11001001 .
|
Решение:
|
|
|
Ответ:
|
|
11001010
|
2.
|
Задача:
|
|
Добавьте бит чётности к следующему сообщению: 10100001 .
|
Решение:
|
|
|
Ответ:
|
|
101000011
|
3.
|
Задача:
|
|
Было принято следующее сообщение: 101011010 . Содержит ли оно ошибку?
|
Решение:
|
|
Нечетное число единиц = ошибка
|
Ответ:
|
|
да
|
1. Теоретический материал
|
Рассмотрим еще подход к обнаружению ошибки – троировании бита в передаваемом сообщении. Пусть имеется один байт 10010010, тогда при передаче сообщения каждый бит будет троирован и сообщение примет вид (111)(000)(000)(111)(000)(000)(111)(000). Скобки в примере применены для наглядности представления записи. Каждая скобка соответствует одному биту исходного сообщения закодированного по методу троирования. Искажение одного бита в скобке позволит выявить возникшие ошибки (101)=1, (100)=0.
|
2. Пример
|
1.
|
Задача:
|
|
Используя кодирование с избытком, закодируйте следующее сообщение: 10101101, троированием битов.
|
Решение:
|
|
111
|
000
|
111
|
000
|
111
|
111
|
000
|
111
|
|
Ответ:
|
|
111000111000111111000111
|
2.
|
Задача:
|
|
В предположении, что в трех идущих подряд битах не может быть более одной ошибки, восстановите следующее сообщение: 101000111001111101001111 .
|
Решение:
|
|
до
|
101
|
000
|
111
|
001
|
111
|
101
|
001
|
111
|
после
|
111
|
000
|
111
|
000
|
111
|
111
|
000
|
111
|
результат
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
|
Ответ:
|
|
10101101
| |
 Скачать 374.5 Kb.
Скачать 374.5 Kb.