Главная страница
Навигация по странице:

  • 10111

  • З адание 2

  • X

  • Y

  • Задание 3

    		•

    Бухалова сети. 10111(2) Прямой код 15(10) Z10010111


    Скачать 112.93 Kb.
    Название10111(2) Прямой код 15(10) Z10010111
    Дата04.09.2022
    Размер112.93 Kb.
    Формат файлаdocx
    Имя файлаБухалова сети.docx
    ТипДокументы
    #660982

    Задание 1. Выполнить арифметические действия, рассматривая операнды как ЧФЗ справа от МЗР в формате одного байта. Определить модуль результата. Формат результата – 2 байта.



    Операция сложения:

    Z=X+Y=20(10)+43(10)=63(10)

    X=20(10) =10100(2); Y=43(10)= 101011(2)

    Z = 0001.0100+0010.1011=111111 = 63

    Операция вычитания:

    Z=X-Y=20(10)-43(10)=-23(10)

    X=20(10) =10100(2);

    Y=-43(10)= 101011(2) Прямой код переводим в дополнительный

    Y= 11010101(2)

    00010100 + 11010101 = 11101001(2) Дополнительный код переводим в прямой
    11101001(2) Инверсия всех разрядов, исключая знаковый

    10010110 +00000001 = 10010111(2) Прямой код = -15(10)

    Z=10010111(2) = 15(10)
    Операция умножения:

    Z=X*Y=20(10)*43(10)=860 (10)




    Z=00001101011100(2)=860(2)

    З адание 2. Выполнить арифметические действия, рассматривая операнды как ЧПЗ с основанием 2 в следующем формате: несмещенный порядок – 4 бита, мантисса – 8 бит. Формат результата – тот же. Округление
    производить после приведения операнда к нормализованной форме. Результат нормализовать.


    X=20.34 Y=43.20

    Преобразуем дробную часть X, равную 0.34 в двоичное число

    2*0.34 = 0.68 0

    2*0.68 = 1.36 1

    2*0.36 = 0.72 0

    2*0.72 = 1.44 1

    2*0.44 = 0.88 0

    2*0.88 = 1.76 1

    2*0.76 = 1.52 1

    2*0.52 = 1.04 1
    0.34(10)=0.01010111(2), а Y=20.34 = 00010100.01010111(2)

    Представим X в формате ЧПЗ, округлив значение мантиссы до 8 разрядов (ненормализованное число)

    X = 0000*10100.011

    PнормХ = Pх + 5

    X = 0101*0.10100011
    Преобразуем дробную часть Y, равную 0.20 в двоичное число

    2*0.20 = 0.40 0

    2*0.40 = 0.80 0

    2*0.80 = 1.60 1

    2*0.60 = 1.20 1

    2*0.20 = 0.40 0

    2*0.40 = 0.80 0

    2*0.80 = 1.60 1

    2*0.60 = 1.20 1
    0.20(10)=0.00110011(2), а Y=43.20 = 00101011.00110011(2)

    Представим Y в формате ЧПЗ, округлив значение мантиссы до 8 разрядов (ненормализованное число):

    Y = 0000*101011.01

    PнормY = Yх + 6

    Y = 0110*0.10101101
    Сложение:

    Z=X+Y= 20.34(10) + 43.20(10) = 63.54(10).

    Y = 0110 0.10101101

    X = 0101 0.10100011
    0110 0.01010001

    + 0.10100011

    0.11110100

    Z = 0110*0.11110100 = 26*0.953125 = 63.5(10)
    Операция вычитания

    Z = X-Y = 20.34-43.20 = -22.86 (10)
    X = 20.34 0101 0 10100011

    0110 0 01010001
    Y= -43.20 0110 1 10101101 ПК

    0110 1 01010011 ДК

    +

    0110 0 01010001 Х

    0110 1 10100100

    0110 1 01011011 Инверсия

    Z = (-) 0110*0.01011011=-26*0.3571875=-22.86(10)

    Операция умножения:

    Z=X*Y=20.34*43.20=878.688

    X= 0101 0.10100011 Y= 0110 0.10101101

    Перемножим мантиссы сомножителей (вариант умножения младшими разрядами вперед):

    qx=0.10100011

    qy=0.10101101
    10100011 P1

    010100011 Сдвиг вправо

    +00000000 P2

    010100011 Сумма P1,P2
    00101000 11 Свдиг вправо

    +10100011 P3

    1100101111 Сумма P1,P2,P3
    01100101 111 Сдвиг вправо

    +10100011 P4

    10001000111 Сумма P1,P2,P3,P4

    00100010 00111 Сдвиг вправо на 2 разраяда (P5)

    +10100011 P6

    1100010100111 Сумма P1,P2,P3,P4,P5,P6

    00110001 0100111 Сдвиг вправо на 2 разряда (P7)

    +10100011 P8

    11010100 0100111 Сумма P1,P2,P3,P4,P5,P6,P7,P8

    011010100 0100111
    Сложим порядки множителей

    0101 px

    0110 py

    1011 px+py

    Нормализуем произведение

    Pнорм = 1010 0.11010100

    Z= 1010*0.11010100 = 210*0.85809375 = 878.688(10)

    Задание 3. Выполнить арифметические действия над операндами,
    представив их в двоично-десятичном коде.


    Операция сложения:

    Z=X+Y=204+432=636

    X = 204(10) =0010 0000 0100(2-10) Y=432(10)= 0100 0011 0010(2-10)
    0010 0000 0100 X

    +0100 0011 0010 Y

    0110 0011 0110 X+Y
    Z= 011000110110(2-10) = 636(10)
    Операция вычитания:

    Z=X-Y=204(10)-432(10)=-228(10)
    Представим |Y| в ДК с избытком 6

    Yок 1011 1100 1101

    0001

    Yдк 1011 1100 1110
    Хпк 0010 0000 0100

    Yдк+ 1011 1100 1110

    Zдк’ 1101 1101 0011
    Zдк’ 1101 1101 0011

    Z̅дк’ 0010 0010 1100

    + 0010

    Zпк’ 0010 0010 1110
    Zпк’ 0010 0010 1110

    +0000 0000 1010

    0010 0010 1000

    Z = 0010 0010 1000(2-10) = -228(10)

    Операция умножения:

    Z=X*Y=204*432=88128

    X = 204(10) =0010 0000 0100(2-10) Y=432(10)= 0100 0011 0010(2-10)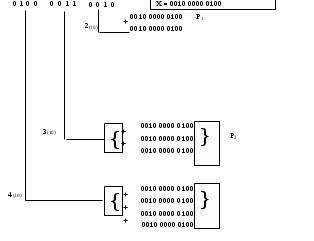



    0010 0000 0100 первое слагаемое P1

    +0010 0000 0100 второе слагаемое P1

    0100 0000 1000 P1 коррекции не требуется
    0010 0000 0100 первое слагаемое P2

    +0010 0000 0100 второе слагаемое P2

    0100 0000 1000

    +0010 0000 0100 третье слагаемое P2

    0110 0000 1100 P2 коррекции не требуется

    0010 0000 0100 первое слагаемое P3

    +0010 0000 0100 второе слагаемое P3

    0100 0000 1000

    +0010 0000 0100 третье слагаемое P3

    0110 0000 1100

    +0010 0000 0100 четвертое слагаемое P3

    1000 0001 0000 требуется коррекция

    +0000 0000 0110

    1000 0001 0110 P3
    P1 0000 0000 0100 0000 1000

    P2+ 0000 0110 0000 1100

    0000 0110 0100 1100 1000

    P3+ 1000 0001 0110

    1000 0111 1010 1100 1000

    + 0000 0000 0110 0110 0000 коррекция

    1000 1000 0001 0010 1000
    Z= 1000 1000 0001 0010 1000(2-10) = 88128(10)

    написать администратору сайта