|
|
Рабочая тетрадь 6-1. Рабочая тетрадь 6
Рабочая тетрадь № 6
Релейно-контактная схема представляет собой схематическое изображение некоторого устройства, состоящего из переключателей, соединяющих их проводников, входов в схему и выходов из нее. В релейно-контактной схеме любой переключатель имеет только два состояния: замкнутое и разомкнутое.
|
1. Теоретический материал
|
Простейшая схема состоит из одного переключателя X, одного входа и одного выхода. Переключателю X ставится в соответствие высказывание x – «Переключатель X замкнут». Если x истинно, то схема проводит электрический ток, в противном случае – не проводит. Если принимать во внимание только значение высказывания, то любому высказыванию x можно поставить в соответствие следующую двухполюсную релейно-контактную схему

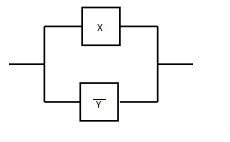
Отрицание высказывания x будем изображать двухполюсной схемой

Конъюнкцию двух высказываний x и y можно представить двухполюсной схемой с последовательным соединением переключателей X и Y
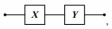
а дизъюнкцию – двухполюсной схемой с их параллельным соединением
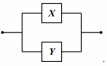
Любая формула алгебры логики может быть представлена в нормальной форме, следовательно, любой формуле алгебры логики можно поставить в соответствие некоторую релейно-контактную схему, и наоборот, каждой релейно-контактной схеме можно поставить в соответствие некоторую формулу алгебры логики.
|
2. Пример
|
Задача:
|
|
Дана логическая формула 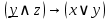 . Составьте для неё релейно-контактную схему. . Составьте для неё релейно-контактную схему.
|
Решение:
|
|
Упросим логическую формулу:
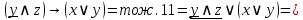
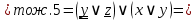
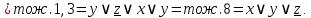
Таким образом, релейно-контактная схема будет иметь следующий вид:
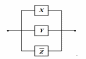
|
Задача:
|
|
Упростить релейно-контактную схему:
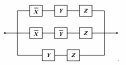
|
Решение:
|
|
Заменим релейно-контактную схему на логическую формулу:
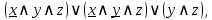
и упростим её:
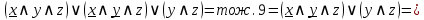
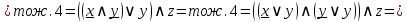
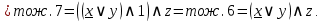
Теперь заменим упрощённую логическую формулу обратно на релейно-контактную схему:
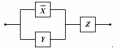
|
Задача:
|
|
Составить релейно-контактную схему, соответствующую импликации.
|
Решение:
|
|
Выразим операцию импликации через основные логические операции «И», «ИЛИ» и «НЕ»:
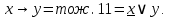
Построим по логической формуле контактно-релейную схему:
|
Задача:
|
|
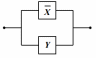
Дана логическая формула:
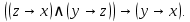
Составьте для неё релейно-контактную схему.
|
Решение:
|
|
Упростим логическую формулу с помощью равносильных преобразований:
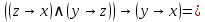
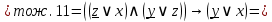
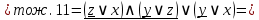
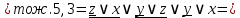
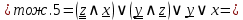
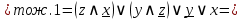
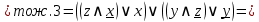
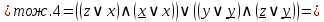
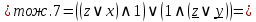
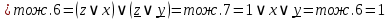
Составим по упрощённой логической формуле контактно-релейную схему:
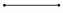
|
Задача:
|
|
Построить релейно-контактную схему, соответствующую f(x, y, z), если известно, что: f(1, 0, 0) = f(0, 1, 1) = f(0, 1, 0) = f(0, 0, 0) = 1.
Для остальных комбинаций аргументов значения функции равны нулю.
|
Решение:
|
|
Составим таблицу истинности для 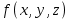 и запишем по ней СДНФ. и запишем по ней СДНФ.
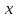
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
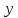
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
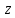
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
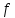
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
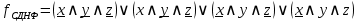
Упростим получившуюся СДНФ:
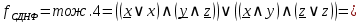
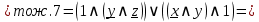
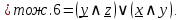
Теперь построим контактно-релейную схему.
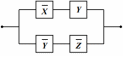
|
Задача:
|
|
Упростить релейно-контактную схему:
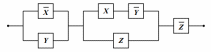
|
Решение:
|
|
По контактно-релейной схеме запишем логическую формулу и далее упростим её:
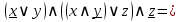
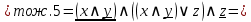
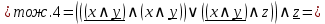
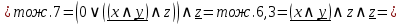
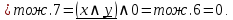
Составим по упрощённой логической формуле контактно-релейную схему.

|
Задача:
|
|
Доказать равносильность следующих релейно-контактных схем:
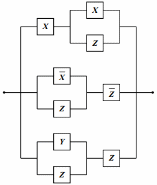
и
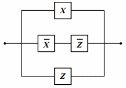
|
Решение:
|
|
Запишем для каждой контактно-релейной схему логическую формулу и упростим их для дальнейшего сравнения.
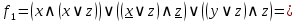
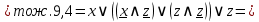
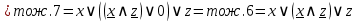
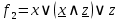
Видно, что  , а следовательно они эквиваленты. Отсюда контактно-релейные схемы также эквивалентны. , а следовательно они эквиваленты. Отсюда контактно-релейные схемы также эквивалентны.
|
3. Задания
|
1.
|
Задача:
|
|
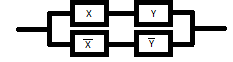
Составить релейно-контактную схему, соответствующую эквивалентности.
|
Решение:
|
|
        x ↔ y =( x → y) & ( y → x) = ( x ∨ y) & ( x ∨ y) = x & x ∨x& y ∨ x & y ∨y& y = x & y ∨ x & y x ↔ y =( x → y) & ( y → x) = ( x ∨ y) & ( x ∨ y) = x & x ∨x& y ∨ x & y ∨y& y = x & y ∨ x & y
|
2.
|
Задача:
|
|
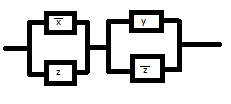
Составить релейно-контактные схемы, соответствующие следующим формулам:
1) 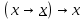 ; ;
2) 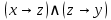 . .
|
Решение:
|
|
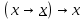 = (¬x∨¬x)→x = ¬x→x =¬¬x∨x= x∨x=x = (¬x∨¬x)→x = ¬x→x =¬¬x∨x= x∨x=x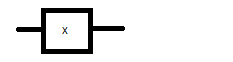
2) 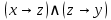 = (¬x ∨ z) & (¬z ∨ y) = (¬ x ∨ z) & ( y ∨¬z) = (¬x ∨ z) & (¬z ∨ y) = (¬ x ∨ z) & ( y ∨¬z)
|
3.
|
Задача:
|
|
Построить релейно-контактные схемы для логических функций 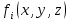 если известно, что: если известно, что:
1) 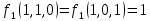 ; ;
2) 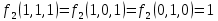 ; ;
3) остальные значения функций 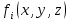 равны нулю. равны нулю.
|
Решение:
|
|
x&y& ¬z∨x&¬y&z =x& (y&¬z∨¬y&z) = x & ( y ∨¬y) & ( y ∨ z) & (¬y ∨¬z) & (z ∨¬z) = x & ( y ∨ z) & (¬y ∨¬z)
x&y&z∨x&∨ ¬y&z∨ ¬x&y& ¬z = x& (y∨ ¬y) &z∨ ¬x&y& ¬z = x&z∨ ¬x&y& ¬z
|
4.
|
Задача:
|
|
Упростите релейно-контактную схему:
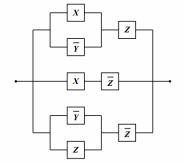
|
Решение:
|
|
( x ∨¬y) & z ∨ x &¬z ∨ (¬y ∨ z) &¬z = x & z ∨¬y & z ∨ x &¬z ∨¬y &¬z ∨z&¬z = x & (z ∨¬ z) ∨¬y & z ∨¬ y & z ∨ 0 = x ∨¬y & (z ∨¬z) = x ∨¬y
|
5.
|
Задача:
|
|
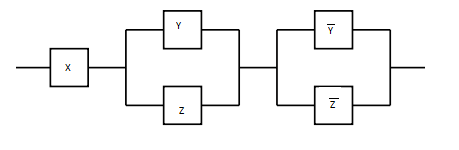
Докажите эквивалентность следующих релейно-контактных схем:
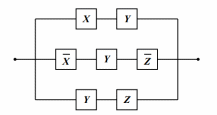
и

|
Решение:
|
|
F1≡x&y∨¬x&y&¬z∨y&z
F2=y
F1= x&y∨ ¬x&y& ¬z∨y&z≡y& (x∨ ¬x& ¬z∨z) ≡y& (( x∨ ¬x) & ( x∨ ¬z) ∨z) ≡y& ( x∨ ¬z∨z) ≡y& 1 ≡y≡F2
| |
|
|
 Скачать 1.6 Mb.
Скачать 1.6 Mb.