|
|
Рабочая тетрадь 6. Рабочая тетрадь 6
1. Теоретический материал
|
Любое вычислительное устройство состоит из набора так называемых «вентилей» – минимальных логических устройств, способных преобразовывать входные сигналы в выходные. Ниже в таблице 1 представлены основные обозначения логических вентилей в различных стандартах.
Таблица 1 – Логические вентили и их условные графические обозначение в стандартах «ГОСТ 2.743-91», «IEC 60617-12: 1997» и «US ANSI 91-1984»
Название вентиля
|
Условные графические обозначения (УГО)
|
ГОСТ 2.743-91
|
IEC 60617-12: 1997
|
US ANSI 91-1984
|
НЕ
|

|

|

|
И
|

|

|

|
ИЛИ
|

|

|

|
НЕ И
|

|

|

|
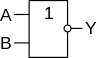
НЕ ИЛИ
|
|

|

|
исключающее ИЛИ
|

|
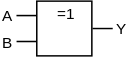
|

|
Маленькие кружочки в УГО обозначают инверсию сигнала (т.е. отрицание НЕ). Они могут стоять и на входе вентиля, обозначая инверсию входного сигнала.
Рассмотрим первое простое устройство, которое можно собрать на вентилях: полусумматор. Его таблица истинности и схема представлена на рисунке 1.
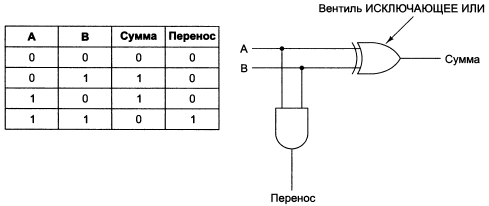
Рисунок 1 – Таблица истинности для сложения одноразрядных чисел
и схема полусумматора
Полусумматор предназначен для нахождения суммы двух бит. При необходимости сложения чисел, состоящих из двух и более разрядов, эта схема уже не работает (нельзя просто взять необходимое число полусумматоров, т.к. в этой схеме не предусмотрен учёт переноса из младшего разряда в старший). Для этого нужно уже соединять между собой так называемые полные сумматоры. Таблица истинности и схема полного сумматора представлена на рисунке 2.
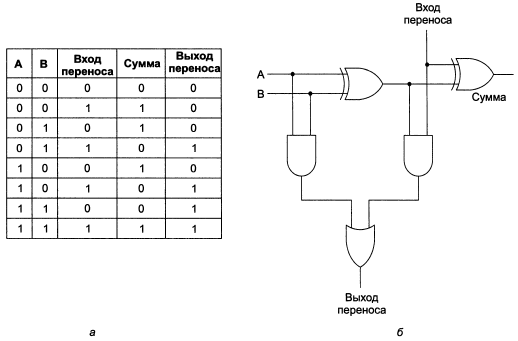
Рисунок 2 – Таблица истинности для полного сумматора (а);
схема для полного сумматора (б)
В вычислительной технике также можно встретить применение мультиплексоров. Мультиплексор имеет один выход и две группы входных линий: информационные и адресные. Код, подаваемый на адресные линии, определяет, какой из информационных входов в данный момент подключен к выходному выводу. Поскольку n-разрядный двоичный код может принимать 2n значений, то если число адресных входов мультиплексора равно n, число его информационных входов должно равняться 2n. УГО мультиплексора с 8 информационными входными линиями 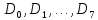 , 3 адресными входными линиями , 3 адресными входными линиями 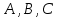 и 1 выходной линией и 1 выходной линией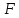 приведено на рисунке 3. приведено на рисунке 3.
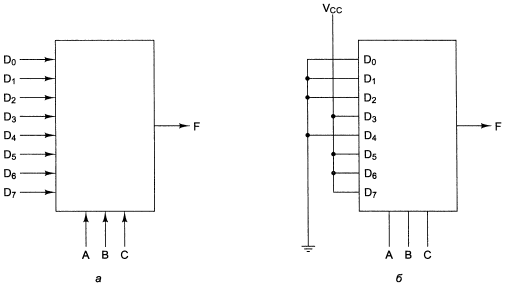
Рисунок 3 – Мультиплексор 8 в 1
Используя мультиплексор можно реализовывать логические функции (пример ниже).
|
2. Пример
|
1.
|
Задача:
|
|
Нарисовать схему (от руки или в любом графическом редакторе), реализующую следующую логическую функцию:
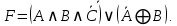
|
Решение:
|
|
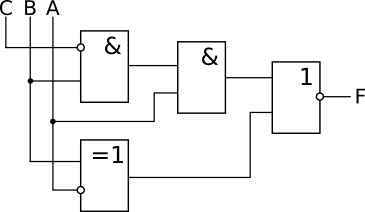
|
2.
|
Задача:
|
|
Записать логическую формулу (формулы) и таблицу истинности для следующей схемы:
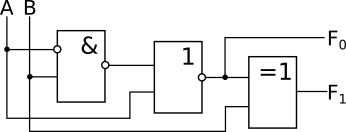
|
Решение:
|
|
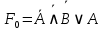 , ,
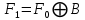 . .
A
|
B
|
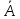
|
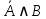
|
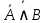
|
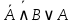
|
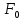
|
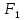
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
|
3.
|
Задача:
|
|
Нарисовать схему (от руки или в любом графическом редакторе), позволяющую суммировать трёхбитовые двоичные числа (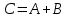 , , 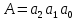 , , 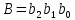 и C и C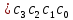 ). ).
|
Решение:
|
|
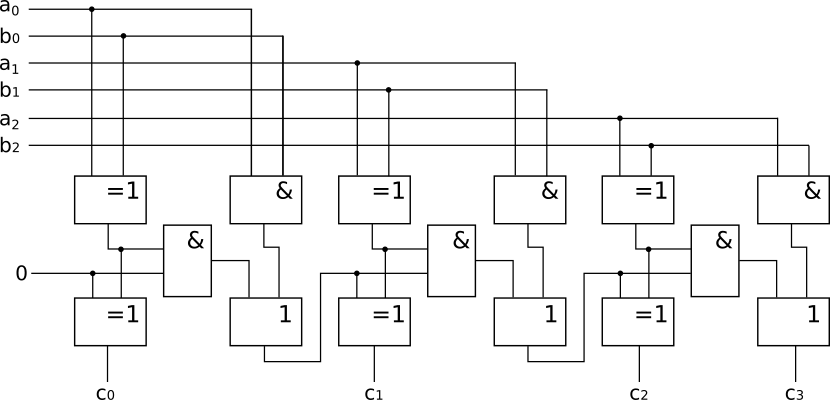
|
4.
|
Задача:
|
|
Используя мультиплексор, нарисовать схему (от руки или в любом графическом редакторе), реализующую функцию большинства от трёх логических переменных.
|
Решение:
|
|
Таблица истинности для функции большинства
|
Схема, реализующая необходимую логическую функцию
|
A
|
B
|
C
|
F
|

|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
|
3. Задания
|
1.
|
Задача:
|
|
Нарисовать схему (от руки или в любом графическом редакторе), реализующую следующую логическую функцию:
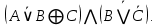
|
Решение:
|
|
|
2.
|
Задача:
|
|
Записать логическую формулу (формулы) и таблицу истинности для следующей схемы:
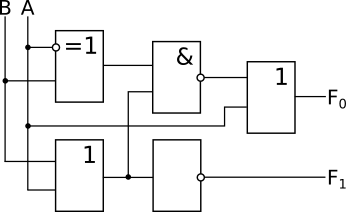
|
Решение:
|
|
|
3.
|
Задача:
|
|
Используя мультиплексор, нарисовать схему (от руки или в любом графическом редакторе), реализующую функцию импликации 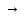 . .
|
Решение:
|
|
|
4.
|
Задача:
|
|
Нарисовать схему (от руки или в любом графическом редакторе), позволяющую умножать двухбитовые двоичные числа.
|
Решение:
|
|
| |
|
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.