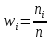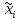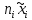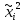рабочая тетрадь. Рабочая тетрадь по математической
 Скачать 40.36 Kb. Скачать 40.36 Kb.
|
|
РАБОЧАЯ ТЕТРАДЬ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ Студента ____________________________ (Фамилия И.О.) Группа _________ Вариант № ________  Оценка ________________________ Преподаватель__________________ Оценка ________________________ Преподаватель__________________   План выполнения типового расчёта План выполнения типового расчётаПостроение статистического распределения выборки. Вычисление точечных оценок математического ожидания и дисперсии. Построение гистограммы относительных частот. Проверка гипотезы о нормальном распределении случайной величины. Нахождение доверительных интервалов для математического ожидания и дисперсии. Перед началом выполнения типового расчёта по математической статистике повторите (или изучите) следующие темы. Дискретные случайные величины. Закон распределения вероятностей дискретной случайной величины. Числовые характеристики дискретной случайной величины. Непрерывные случайные величины. Функция распределения, плотность распределения, их взаимосвязь и свойства. Нормальный закон распределения непрерывных случайных величин, правило «трех сигм». Числовые характеристики непрерывных случайных величин. Генеральная совокупность и выборка. Вариационный ряд. Гистограмма, эмпирическая функция распределения выборки. Статистическое оценивание параметра распределения по выборке. Точечные оценки и их характеристики: несмещённость, эффективность, состоятельность. Интервальные оценки. Доверительные интервалы. Интервальное оценивание параметров нормального распределения. Статистические гипотезы, их виды. Понятие о проверке статистических гипотез. Ошибки 1-го и 2-го рода. Критерий согласия Пирсона. Построение статистического распределения выборкиДанную выборку преобразуйте в вариационный (интервальный) ряд. Для этого: 1. Упорядочите выборку, т.е. запишите все значения 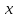 случайной величины случайной величины 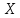 в возрастающем порядке. Если какое-либо значение повторяется, запишите его столько раз, сколько оно Вам встретилось. в возрастающем порядке. Если какое-либо значение повторяется, запишите его столько раз, сколько оно Вам встретилось.
2. Вычислите объем выборки 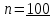 ; минимальное значение ; минимальное значение 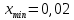 ; максимальное значение ; максимальное значение 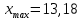 . .3. Разбейте диапазон изменения случайной величины 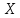 на интервалы. Число интервалов определяется по формуле на интервалы. Число интервалов определяется по формуле 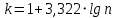 с округлением до ближайшего целого: с округлением до ближайшего целого: 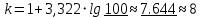 . .Ширину каждого интервала 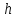 выберите с точностью выборки и округлите в сторону завышения выберите с точностью выборки и округлите в сторону завышения 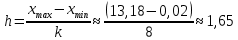 Границы интервалов вычислите по формулам 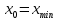 , , 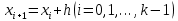 . .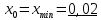 ; ; 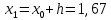 ; ; 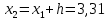 ; ; 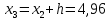 ; ;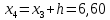 ; ;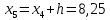 ; ;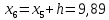 ; ;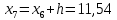 ; ; 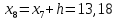 . .4. Вычислите частоту каждого интервала 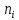 – количество элементов – количество элементов 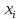 , попавших в , попавших в 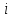 -й интервал. Если элемент совпадает с границей интервала, то он относится к интервалу с меньшим порядковым номером. -й интервал. Если элемент совпадает с границей интервала, то он относится к интервалу с меньшим порядковым номером.5. Вычислите относительные частоты интервалов по формулам 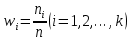 . .Полученные данные занесите в четыре первые столбца таблицы 1. Вычисление точечных оценок математического ожидания и дисперсииДля вычисления оценок заполните таблицу 1. Здесь 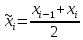 Таблица 1
|