Организация и планирование эксперимента. Работа 5. Гудков А.В. НМТМ-122201. Работа 5. Полный факторный эксперимент первого порядка
 Скачать 27.69 Kb. Скачать 27.69 Kb.
|
|
Работа №5. Полный факторный эксперимент первого порядка Целью эксперимента является определение зависимости скорости нагрева металла в мартеновской печи y(Vi) от величины абсолютного избытка воздуха X1( 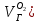 и тепловой нагрузки X2(Qт) в период чистого кипения. и тепловой нагрузки X2(Qт) в период чистого кипения.Уравнение регрессии имеет следующий вид 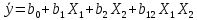 . (1) . (1)Выбираем уровни варьирования факторов из соображений возможности реализации опытов в пределах технологических ограничений и получения значимых эффектов, превышающих ошибки эксперимента (табл. 2). Таблица 2 – Уровни варьирования факторов
Составляем матрицу планирования и карту проведения эксперимента (табл. 3). Таблица3 – Таблица полного факторного эксперимента для двух факторов
После составления матрицы планирования проводится эксперимент на выбранном объекте исследования. Опыты проводятся в случайном порядке в соответствии с принципом рандомизации. В нашем случае в первой серии опытов первым был реализован опыт с порядковым номером 4, в котором избыток воздуха и тепловая нагрузка поддерживались на верхних уровнях, при этом получена скорость нагрева 97 °C/ч, вторым реализован опыт номер 1, в котором оба фактора X1и X2поддерживались на нижних уровнях, а скорость нагрева оказалась равной 60 °C/ч, и т.д. Таким образом, после проведения двух серий опытов (в каждой по четыре опыта с неповторяющимися комбинациями уровней факторов) оказались заполненными столбцы значений выхода 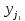 и и 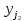 . .Теперь есть все необходимое для обработки и статистического анализа результатов эксперимента. Теперь есть все необходимое для обработки и статистического анализа результатов эксперимента. Рассчитывают построчные средние, функция СРЗНАЧ 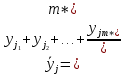 , (16) , (16)где 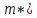 – число повторных опытов. – число повторных опытов.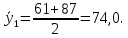 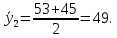 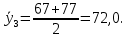 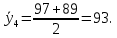 Результаты расчета заносят в столбец 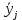 карты проведения эксперимента (табл. 3). карты проведения эксперимента (табл. 3).Далее определяются построчные дисперсии (дисперсии воспроизводимости), функция ДИСП.В 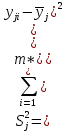 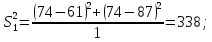 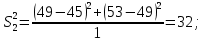 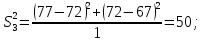 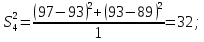 Сумма построчных дисперсий: 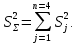 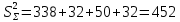 . .Проверяют воспроизводимость опытов по критерию Кохрена. рассчитывается экспериментальное значение критерия 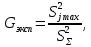 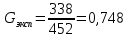 теоретическое значение G;m;n. Для =0,05, m=m*-1=2-1 и n=4 значение G0,05;1;4=0,9096. из сравнения экспериментального и теоретического значения критерия Кохрена делается заключение об однородности дисперсий. В случае неравноточности опытов необходимо увеличить число повторных экспериментов или повысить их точность. Осуществляется расчет коэффициентов в уравнении регрессии: 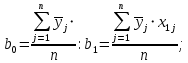 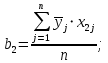 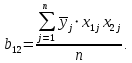 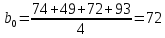 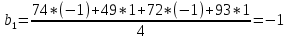 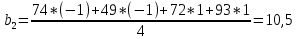 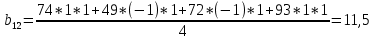 Осуществляется проверка значимости коэффициентов регрессии. Предварительно определяется дисперсия воспроизводимости (дисперсию отклика): 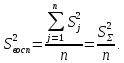 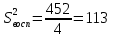 Дисперсия коэффициентов уравнения регрессии 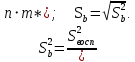 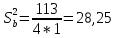 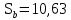 Находится значение доверительного интервала для коэффициентов регрессии 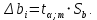 Здесь m=n(m*-1)=4(2-1)=4, тогда теоретическое значение критерия Стьюдента t0,05;4=2,78. 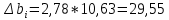 Коэффициент значим, если его абсолютное значение больше доверительного интервала, т.е. коэффициент должен быть больше ошибки его определения. В результате определения уравнения регрессии может получиться так, что один (или несколько) коэффициентов не очень большие и окажутся незначимыми. Факторы, имеющие коэффициенты, незначимо отличающиеся от нуля, могут быть выведены из состава уравнения, так как их влияние на параметры отклика будет отнесено к ошибке эксперимента. Учитывая ортогональность плана, оставшиеся коэффициенты уравнения регрессии можно не пересчитывать. Результаты расчета выходных параметров по уравнению полученной модели 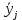 заносятся в табл. 3. заносятся в табл. 3.Проверяют адекватность (пригодность) модели, т.е. насколько хорошо полученное уравнение описывает результаты эксперимента в исследуемой области. Для этого применяют критерий Фишера F | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

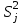 ,
,