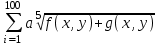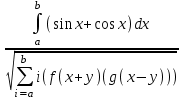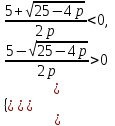Лабораторная работа номер 4. Лабораторная работа Лучина 4. Работа с редактором формул Microsoft Equation 0

• Название: Работа с редактором формул Microsoft Equation 0
• Анкор: Лабораторная работа номер 4
• Дата: 18.10.2021
• Размер: 41.16 Kb.
• Имя файла: Лабораторная работа Лучина 4.docx
• Тип: Лабораторная работа; #250138

Лабораторная работа №4
Тема: Работа с редактором формул Microsoft Equation 3.0
Цель работы: научится работать с редактором формул Microsoft Equation 3.0

Оборудование: IBM PC

Порядок выполнения работы.

1. 
   Используя средства Редактора формул, создать документы с формульными фрагментами:
   

а) по образцу 1;

б) по образцу 2;

б) по образцу 3 (воспользоваться только средствами Microsoft Word, а не редактора формул);

в) по образцу 4 (воспользоваться только средствами Microsoft Word, а не редактора формул);

г) по образцу 5;

д) по образцу 6;

2. 
   Оформить формулы, созданные по предлагаемым образцам, следующим образом:
   

а) вставить формулу в рамку;

б) оттенить формулу фоном.

Результат сохранить в своей папке (каждый образец в отдельный файл).

Образец 1 ФОРМУЛА 1

ФОРМУЛА 2

Образец 2 Система неравенств

Образец 3 H2SO4 — серная кислота H2SO3 — сернистая кислота H2S — сероводород BaSO4 — сульфат бария NaOH — гидрат натрия H2O – вода

Образец 4

Формальной грамматикой называется четверка

<V_N, V_T, P, >,

где V_N – конечное множество нетерминальных символов;

V_T – конечное множество терминальных символов;

P – конечное множество правил подстановки;

P={, где V_N, (V_N U V_T)⁺};

 – аксиома грамматики; V_N.

Образец 5

Теорема. Решение уравнения (1) содержит max(0,) + max(0,) – r произвольных комплексных постоянных и находится по формуле: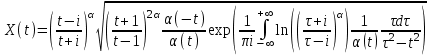



Представим матрицу S^A,B в виде: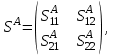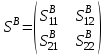



Образец 6

Электродинамические свойства специальных блоков перехода описываются матрицей рассеяния вида:

S_n =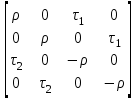

с элементами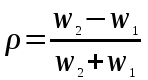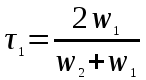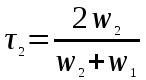

, , ,

где W₁ и W₂ – волновые сопротивления граничащих сред, связанные с материальными параметрами сред, заполняющих блоки, соотношениями:

W_1,2 = .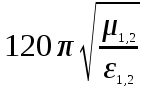

Блоки контакта с границей имеют выход на один виртуальный волновод и описываются матрицей рассеяния

S_b = ,

где r = -1 для идеально проводящей стенки и r = 1 для идеальной магнитной стенки. Конечная проводимость металла может быть учтена путем использования в матрице рассеяния коэффициента отражения r вида:

r =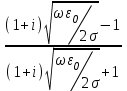

3. 
   Показать выполненную работу преподавателю, оформить отчет о проделанной работе.
   
4. 
   Закрыть все программы, выключить компьютер