расчет цепи постоянноготока. Расчет цепей постоянного тока

• Название: Расчет цепей постоянного тока
• Анкор: расчет цепи постоянноготока
• Дата: 22.11.2020
• Размер: 70.49 Kb.
• Имя файла: Prakticheskoe_Raschet_tsepi_postoyannogo_toka.docx
• Тип: Контрольная работа; #152735

15.05.2020 г Практическое занятие гр. ТЭО-19з

Тема: Расчет цепей постоянного тока

Контрольная работа содержит задачи соответствующие изученным разделам и темам. После изучения цепей постоянного тока студент должен уметь:

- по индивидуальным заданиям определить эквивалентное сопротивление электрической цепи со смешанным соединением элементов.

- произвести расчет электрической цепи, применяя законы Ома и Кирхгофа, составить баланс мощностей. В контрольной работе для этого заданы задачи 1 и 2.

Электрические цепи подразделяют на простые и сложные. К признакам, определяющим простую цепь, можно отнести:

- наличие только одного источника энергии;

- возможность до расчётов указать истинные направления токов во всех ветвях;

- соединение элементов цепи выполнено по правилам последова­тельного, параллельного и смешанного соединений.

Отсутствие любого из этих признаков может переводить цепь в категорию сложных.

Для расчета простых цепей используется метод свёртки (упрощения) схемы цепи относительно зажимов источника (он же метод эквивалентного сопротивления) При свертывании следует знать и учитывать свойства способа соединения элементов цепи между собой. Свертка нужна в том случае, если в задаче дана ЭДС источника или напряжение на его зажимах. А для определения тока в каждом сопротивлении надо знать его напряжение. Свернув схему узнают эквивалентное сопротивление всей цепи к которому и приложено напряжение или ЭДС источника. Теперь можно узнать ток, вытекающий из источника, затем выполнить расчет других токов. Для всех узловых точек можно проверять себя, используя 1закон Кирхгофа. Сумма токов втекающих в узел, равна сумме вытекающих токов. Направления токов в схеме задает источник. Стрелка ЭДС направлена к клемме + источника. И токи от этой клеммы растекаются по всем ветвям и возвращаются к клемме – источника. Если источник не показан на схеме, то + выбираем сами произвольно. Индексы токов обычно присваивают такими, как у сопротивлений по которым они протекают. Перед решением задач посмотрите примеры задач с решениями.

Если в задаче даны ток или напряжение на каком- либо сопротивлении, то решение начинают с этого участка. Затем изучают соседние участки, и используя свойства последовательного или параллельного соединений как бы развертывают схему и находят другие токи и напряжения.

Пример 1 Дана электрическая цепь постоянного тока. Необходимо найти эквивалентное сопротивление R_ЭКВ.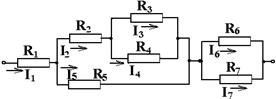
 

1.Для этого на параллельно соединенных резисторах R₃ и R₄ найдем их общее сопротивление: их произведение разделим на их сумму:

R₃₄ = (R₃ ∙ R₄) / (R₃ + R₄)

Затем точно также на параллельных участках R₆ и R₇ найдем их общее сопротивление

R₆₇ = (R₆ ∙ R₇) / (R₆ + R₇)

Резисторы R₂ и R₃₄ соединены последовательно, значит, их надо сложить:

R₂+ R₃₄ = R₂₃₄

Резисторы R₂₃₄ и R₅ соединены параллельно. Поэтому (как для двух параллельных) их произведение разделим на их сумму:

R₂₃₄₅ = (R₂₃₄ ∙ R₅) / (R₂₃₄ + R₅)

Получаем, что резистор R₁ и эквивалентно рассчитанные участки сопротивлениями R₂₃₄₅ и R₆₇ соединены последовательно, их сложим и найдем полное сопротивление, т. е. эквивалентное сопротивление всей цепи:

R_ЭКВ = R₁ + R₂₃₄₅ + R₆₇

2. Зная напряжение (или ток), подведенное к цепи, найдем ток (или напряжение) цепи из закона Ома для участка цепи. U = I∙ R или I = U / R

3. Т. к. участки с сопротивлениями R₁, R₂₃₄₅ и R₆₇ соединены последовательно, то ток на этих участках одинаков:

I₁ = I₂₃₄₅ = I₆₇ = I

4. Значит, можем найти напряжение на этих же участках, умножив ток (ток одинаков на последовательных участках цепи!) на сопротивления участков.

U₁ = I₁∙ R₁

U₂₃₄₅ = I₁∙ R₂₃₄₅ = U₂₃₄ = U₅ , т. к. на параллельных участках цепи напряжение одинаково.

U₆₇ = I₁∙ R₆₇ = U₆ = U₇ , т. к. на параллельных участках цепи напряжение одинаково.

Зная напряжения на резисторе R₅ и участке R₂₃₄, найдем токи на них: I₅ = U₅ / R₅ ; I₂₃₄ = U₂₃₄ / R₂₃₄

Аналогично (заметьте, напряжение на них одинаково, но сопротивление разное, поэтому и токи разные!):

I₆ = U₆ / R₆ I₇ = U₇ / R₇

Проверка: а) должно быть, чтобы сумма токов I₆ и I₇ равно току I₆₇ на этом участке с сопротивлением R₆₇, согласно первому закону Кирхгофа. I₆₇ = I₆ + I₇

б) должно быть, чтобы сумма токов I₂₃₄ и I₅ равно току I₂₃₄₅ на этом участке с сопротивлением R₂₃₄₅,

т. е. I₂₃₄₅ = I₂₃₄ + I₅

Но токи на последовательно соединенных участках R₂ и R₃₄ цепи одинаковы,

т. е. ток I₂ равен току на I₃₄, но I₃₄ = I₃ + I₄ . Запишем это: I₂ = I₃₄ = I₃ + I₄

5. Напряжения на последовательно соединенных участках R₂ и R₃₄ цепи равно сумме напряжений

U₂₃₄ = U₂ + U₃₄ . Но U₃₄ = U₃ = U₄

Зная ток I₂ на R₂, найдем напряжение U₂ на нем U₂ = I₂∙ R₂

Также, зная ток I₃₄, найдем напряжение U₃₄ на участке U₃₄ = I₃₄∙ R₃₄

Проверка. Должно быть, что напряжения U₃₄ = U₃ = U₄ , т. к. напряжение на параллельных участках одинаково. Отсюда найдем из закона Ома токи на резисторах R₃ и R₄.

Пример 2

Определить эквивалентное сопротивление, напряжение, силу тока на каждом участке электрической цепи напряжением 100В. Сопротивления проводников равны: R₁=5,2 Ом, R₂=5 Ом, R₃=4 Ом, R₄=12 Ом, R₅=12 Ом.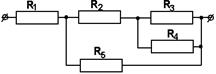

 Рис. 1 Решение.

Первая часть. Резисторы с сопротивлениями R₃ и R₄ соединены параллельно. Заменим их эквивалентным сопротивлением R₃₄.

Тогда получаем: 

Вычислим: R₃₄ = 3 Ом. Получим эквивалентную схему цепи: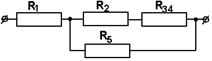

 Рис.2

Сопротивление последовательно соединенных резисторов R₂ и R₃₄равно их сумме:

R₂₃₄ = R₂ + R₃₄.Вычислим:R₂₃₄ = 5 Ом + 3 Ом = 8 Ом.

Эквивалентная схема будет такой: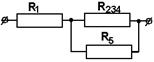

Рис.3

Заменим параллельныеучасткиR₂₃₄ и R₅ эквивалентным сопротивлением R_{234 5}


Вычислим: R_{2 34 5} = 4,8 Ом.

Получим эквивалентную схему:

Сопротивление последовательно соединенных резисторов  R₁ и R_{234 5} равно их сумме: R_{1234 5} = R₁ + R_{234 5}. Вычислим: R₁₂₃₄₅ = 5,2 Ом + 4,8 Ом = 10 Ом.

Эквивалентная схема будет такой:

Получаем эквивалентное (или полное) сопротивление цепи:

R_ЭКВИВ. = R_{1234 5}.= 10 Ом.

Вторая часть. Перейдем к расчету токов и напряжений.

а)Зная полное сопротивление, напряжение цепи можно по закону Ома для участка электрической цепи найдем ток в цепи

 Вычислим: I = 100 В / 10 Ом = 10 А = I₁ = I₂₃₄₅

Т. к. резистор R₁ и участок сопротивлением R_{234 5} соединены последовательно, то токи в них одинаковы, и, значит, равны I = I₁ = I₂₃₄₅ =10 А.

б) Зная сопротивления на R₁и R₂₃₄₅и токи, можем найти напряжения исходя из закона Ома U = I •R, т. е.U₁ =I ∙R₁ иU₂₃₄₅ = I₂₃₄₅ • R₂₃₄₅

Вычислим: U₁ = 10 А • 5,2 Ом = 52 В и U_{234 5} = 10 А • 4,8 Ом = 48 В

в) На параллельных участках R₂₃₄ и R₅напряжения будут одинаковы и равны напряжению

U₂₃₄₅ = U₅ = U₂₃₄ = U₅ = 48 В.

Тогда можем найти ток на последовательно соединенных участках сопротивлениями R₂и R₃₄, где токи одинаковы и равны:I₂ = I₃₄ = U₂₃₄/ R₂₃₄ Вычислим: I₂ = I₃₄ = 48 В / 8 Ом = 6 А.

г)Найдем напряжения на .R₂и R₃₄, исходя из закона Ома.

U₂ =I₂ ∙R₂ и U₃₄ =I₃₄ ∙R₃₄ Вычислим: U₂ =6 А ∙ 5 Ом = 30 В и U₃₄ = 6 А ∙ 3 Ом = 18 В.

Сумма напряжений U₂ и U₃₄должна быть равна напряжению на участкеU₂₃₄,

т. е. U₂ + U₃₄ = U ₂₃₄, так оно и есть: .U₂₃₄ = 48 В = 30 В + 18 В.

д) Напряжения на параллельных резисторахR₃ и R_4, должны быть равны: U₃=U₄ = U₃₄ =18 В

Токи:: I₄ = U₄/ R₄и I₃=U₃ /R₃ Вычислим:I₄ = 18 В / 12 Ом = 1,5 А. I₃ = 18 В / 4 Ом = 4,5 А.

Проверим: т. к. R₃ и R₄ параллельны, то сумма токов I₃ + I₄на этом участке должна быть равна токуI₂ илиI₃₄, т. е. I₂ = I₃₄ = I₃ + I₄ =1,5 А + 4,5 А = 6 А.

е) Зная напряжение U₅ и сопротивление R₅,найдем ток на этом параллельном участке. I₅ = U₅ / R₅ = 48 В / 12 А = 4 А.

Сумма токов (I₂₃₄ +I₅) = I_{234 5} на параллельных участках с сопротивлениями R₂₃₄ и R₅ должна быть равна току на участке R_{234 5} или I₁, т. е. всего участка цепи I = I₁ = I_{234 5} = I₅ +I₂₃₄= 4 А + 6 А = 10 А.

Ответ. Нашли значения эквивалентного (полного) сопротивления, напряжения и токи на всех участках цепи. Записать ответы по порядку.

Пример 3

Дано:R₁ = 30 Ом, R₂ = 70 Ом, R₃ = 19 Ом, R₄ = 40 Ом, U = 40 В

Найти: эквивалентное сопротивление цепи; все токи напряжения на резисторах, если первые два соединены параллельно, третье и четвертое к ним последовательно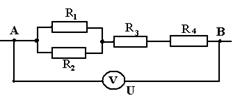

 Решение.

1. R₁ и R₂ соединены параллельно. Найдем сопротивление R₁₂ для этих двух ветвей на этом участке цепи. Оно равно   или полученной преобразованием этой формулы:   . Вычислим: R₁₂= (30 Ом ∙ 70 ом) / (30 Ом + 70 ом) = 21 Ом.

2. Получим эквивалентную схему цепи из проводников R₁₂, R₃ и R₄ , присоединенных последовательно.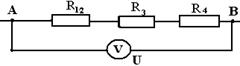



Чтобы найти полное эквивалентное сопротивление всей цепи надо сложить сопротивленияR₁₂, R ₃ и R ₄: R _эквив. = R _АВ =R₁₂₃₄ = R₁₂ +R ₃ + R ₄ = 21 Ом + 19 Ом + 40 Ом = 80 Ом.

Получим эквивалентную схему цепи: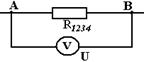



3. Теперь используя закон Ома для участка цепи (сила тока на участке электрической цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна его сопротивлению) I=   . Найдем токи на последовательных участках. Сила тока на последовательных участках цепи одинакова, поэтому:

I_AB =I₁₂= I₃ = I₄ = U_AB / R_AB = 40 B / 80 Ом = 0,5 A

1.Найдем напряжения на участках R₁₂, R₃ и R₄.

Т. к. напряжения на параллельных участках цепи одинаковы, то

U₁₂ = R₁₂ ∙ I₁₂ = U₁ = U₂ = 0,5А ∙ 21 Ом = 10,5 В.

U₃ = R₃ ∙ I₃= 19 Ом ∙ 0,5А = 9,5 В.

U₄ = R₄ ∙ I₄ = 40 Ом ∙ 0,5А = 20 В.

Сумма напряжений на последовательных участках равна напряжению на участке АВ.

Проверим: U_АВ = 10,5 В + 9,5 В + 20 В = 40 В.

2.Найдем силу тока на параллельных ветвях с проводниками R₁ и R₂.
I₁= U₁/ R₁= 10,5B / 30 Oм = 0,35A.

I₂= U₂/ R₂= 10,5 B / 70 Oм = 0,15 А

Проверим правильность того, что сумма токов I₁ + I₂, протекающих по ветвям, равна силе тока в неразветвленной части цепи:

I₁₂ = I₁ + I₂ = 0,35A +0,15 А = 0, 5 А.

3.Запишем полученные ответы.

R _экв. = R _АВ =R₁₂₃₄ = 80 Ом;

I_AB =I₁₂= I₃ = I₄ = 0, 5 А

I₁ = 0,35A

I₂ = 0,15 А

I₁₂ = I₁ + I₂ = 0,35A +0,15 А =0,5 А.

U₃ = 9,5 В

U₄ = 20 В

U₁₂ = U₁ = U₂ = 10,5 В