электрика. РАСЧЕТ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА С МАГНИТНО-СВЯЗАННЫМИ КАТУШКАМИ. Расчет цепи синусоидального тока с магнитносвязанными катушками
 Скачать 133.4 Kb. Скачать 133.4 Kb.
|
|
РАСЧЕТ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА С МАГНИТНО-СВЯЗАННЫМИ КАТУШКАМИ Для электрической схемы, выполнить следующее: 1. Составить и решить систему уравнений по законам Кирхгофа без учета магнитных связей между катушками. 2. Составить и решить систему уравнений по законам Кирхгофа с учетом магнитных связей между катушками. 3. Составить и решить систему уравнений по методу контурных токов с учетом магнитных связей между катушками. 4. Построить векторную диаграмму токов и топографическую диаграмму напряжений вдоль любого контура. 5. Составить уравнение баланса активных и реактивных мощностей.  Рис.1.Схема задания. Дано:  = 10*1 = 10 B = 10*1 = 10 B = 10*4 = 40 B = 10*4 = 40 B = 5*1 = 5 Ом = 5*1 = 5 Ом = 5*2 = 10 Ом = 5*2 = 10 Ом = 5*6 = 30 Ом = 5*6 = 30 Ом 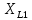 = 3*1 = 3 Ома = 3*1 = 3 Ома = 3*4 = 12 Ом = 3*4 = 12 Ом = 3*6 = 18 Ом = 3*6 = 18 Ом = 4*3 = 12 Ом = 4*3 = 12 Омf = 50 Гц k=0,4 Решение: 1. Составить и решить систему уравнений по законам Кирхгофа без учета магнитных связей между катушками.  Рис.2.Расчётная схема по законам Кирхгофа без учёта магнитных связей. Решаем в символической форме (для действующих значений) Определяем комплексы действующих значений э.д.с. 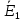 = =  = 10 = 10 B B = =  = 40 = 40 B BСоставим систему уравнений по законам Кирхгофа для двух узлов (“a” и “b”) и трёх контуров   - -  = 0 = 0 - - 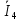 - - = 0 = 0 *( *( + j + j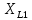 ) + ) +  *(- j *(- j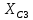 ) = ) = 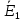 -  *(- j *(- j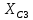 )+ )+ * * + +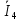 * j * j = =  - 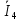 * j * j + +  *( *(  + j + j ) = - ) = -  В  - -  - -  = 0 = 0 - - 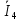 - - = 0 = 0 *( *( + j + j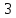 ) + ) +  *(- j *(- j ) = ) =  -  *(- j *(- j )+ )+ * * + +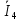 * j * j = =  - 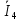 * j * j + +  *( *(  + j + j ) = - ) = -  Решение системы  = 1,13 – j1,46 = = 1,13 – j1,46 =  A A = 1,45 – j1,46 = = 1,45 – j1,46 = 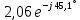 A A = -0,325 – j0,000812 = = -0,325 – j0,000812 =  A A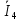 = 1,54 – j2,12 = 2,62 = 1,54 – j2,12 = 2,62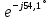 A A = -0,085 +j0,666= 0,672 = -0,085 +j0,666= 0,672 A A2. Составить и решить систему уравнений по законам Кирхгофа с учетом магнитных связей между катушками.  Рис.3.Расчётная схема по законам Кирхгофа с учётом магнитных связей. Реактивное сопротивление взаимоиндукции 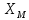 = k* = k*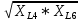 = 0,4* = 0,4* = 5,88 Ом = 5,88 ОмСоставим систему уравнений по законам Кирхгофа для двух узлов (“a” и “b”) и трёх контуров   - -  = 0 = 0 - - 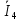 - - = 0 = 0 *( *( + j + j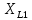 ) + ) +  *(- j *(- j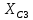 ) = ) = 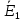 -  *(- j *(- j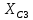 )+ )+ * * + +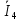 * j * j - -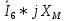 = =  - 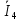 * j * j + +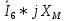 + +  *( *(  + j + j ) - ) -  = - = -  В  - -  - -  = 0 = 0 - - 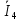 - - = 0 = 0 *( *( + j + j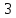 ) + ) +  *(- j *(- j ) = ) =  -  *(- j *(- j )+ )+ * * + +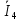 * j * j - -  *j5,88 = *j5,88 =  - 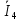 * j * j + + *j5,88 + *j5,88 +  *( *(  + j + j ) - ) - 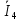 *j5,88 = - *j5,88 = -  Решение системы  = 1,31 – j1,21 = = 1,31 – j1,21 =  A A = 1,48 – j1,2 = = 1,48 – j1,2 =  A A = -0,177 – j0,014 = = -0,177 – j0,014 = 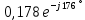 A A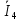 = 1,28 – j1,79= 2,2 = 1,28 – j1,79= 2,2 A A = 0,208 +j0,595= 0,63 = 0,208 +j0,595= 0,63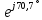 A A3. Составить и решить систему уравнений по методу контурных токов с учетом магнитных связей между катушками.  Рис.4.Расчётная схема методом контурных токов с учётом магнитных связей. 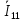  + j + j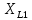 - j - j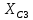 ) + ) + 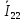 * j * j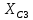 = = 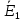 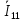 * j * j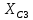 + +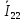 * * + j + j - j - j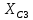 ) + ) + * (-j * (-j - - = =  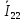 * * + + * ( * ( + j + j = = 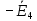 В 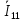 *( *( + j + j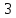 - j - j ) + ) + 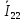 * j * j = =  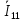 * j * j + +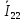 * * + j + j - j - j ) + ) + * (-j * (-j – – = =  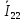 * * + + * ( * ( + j + j = =  Решение системы 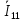 = 1,31 – j1,21 = = 1,31 – j1,21 =  A A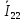 = 1,48 – j1,2 = = 1,48 – j1,2 =  A A = 0,208 +j0,595= 0,63 = 0,208 +j0,595= 0,63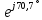 A AТоки ветвей  = =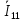 = 1,31 – j1,21 = = 1,31 – j1,21 =  A A = =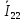 = 1,48 – j1,2 = = 1,48 – j1,2 =  A A = = = 1,31 – j1,21 – (1,48 – j1,2 ) = - 0,177 – j0,014 = = 1,31 – j1,21 – (1,48 – j1,2 ) = - 0,177 – j0,014 = 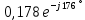 A A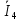 = = = 1,48 – j1,2 –(0,208 +j0,595) = 1,28 – j1,79= 2,2 = 1,48 – j1,2 –(0,208 +j0,595) = 1,28 – j1,79= 2,2 A A = = = 0,208 +j0,595= 0,63 = 0,208 +j0,595= 0,63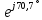 A AПостроить векторную диаграмму токов и топографическую диаграмму напряжений вдоль любого контура. Построим топографическую диаграмму напряжений для внешнего контура для чего рассчитаем напряжения на элементах  = =  * * = =  *5 = *5 = 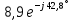 B B = =  *j *j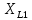 = =  * * = = 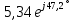 B B = =  * * = =  *10 = *10 =  B B = =  *j *j = 0,63 = 0,63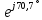 * *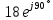 = =  B B = =  * * = 0,63 = 0,63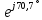 * * = =  B B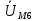 = - = - 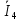 *j *j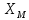 = -2,2 = -2,2 * *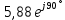 = = B B  Рис.5. Векторная диаграмма токов и топографическая диаграмма напряжений Составить уравнение баланса активных и реактивных мощностей. Мощность источников  = = 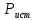 + j + j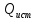 = = 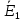 * * + +  * * = 10 = 10 * * +40 +40 *2,2 *2,2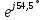 = == 64,1 +j83,8 BA Мощность потребителей Активная 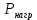 = = 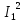 * * + +  * * + +  * * = = 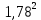 * * + + 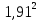 * * + +  * * = 64,1 Вт = 64,1 ВтРеактивная  = = 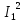 * *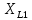 - - 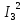 * *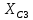 + +  * * + +  * * – 2* – 2*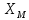 * * *cos( *cos( - -  ) = ) == 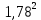 * *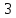 - -  * * + +  * * + +  * * - 2*5,88*2,2*0,63* cos( - 2*5,88*2,2*0,63* cos( ̊ ̊ ) = ) == 83,8 вар Баланс выполняется |
