Практическое задание 1. Расчет деревянных элементов по первой группе предельных состояний на изгиб, сжатие, растяжение и сложное сопротивление
 Скачать 191.19 Kb. Скачать 191.19 Kb.
|
Практическое задание 1Расчет деревянных элементов по первой группе предельных состояний на изгиб, сжатие, растяжение и сложное сопротивление Тема 2.1. Напряженно-деформированное состояние деревянных элементов Задание Выполнить задачи 1.1, 1.2, 1.3 и сделать выводы к каждой задаче. Требования к оформлению практического задания 1: 1. Работа оформляется в программе Microsoft Word. 2. Формулы набираются в редакторе формул. 3. Чертежи выполняются в графическом редакторе (любом) и вставляются в работу. 4. Запрещается вставлять в работу отсканированные (сфотографированные) материалы. Задача 1.1 Расчет центрально-растянутых элементов (расчет на растяжение) 1. Определить несущую способность центрально-растянутого деревянного элемента (рисунок 1) сечением b x h, ослабленного шестью отверстиями, выходящими на пласть, диаметром d с исходными данными согласно варианту. 2. Проверить на прочность по первой группе предельных состояний центрально-растянутый деревянный элемент, если растягивающее усилие N = 70 кН (исходные данные те же). Пример выполнения задачи 1.1 1. Проверить несущую способность центрально-растянутого деревянного элемента (рисунок 1) сечением b x h = 120 мм x 300 мм, ослабленного шестью отверстиями, выходящими на пласть, диаметром d = 16 мм со следующими исходными данными: a = 210 мм; c = 300 мм; е = 120 мм; материал элемента: клен; условия эксплуатации: А1; сорт древесины: 2. Решение 1. Несущую способность элемента при заданных условиях задачи вычисляем по формуле: N = m0 mп mв Rртабл Fнт, где m0 – коэффициент, учитывающий наличие ослаблений, равен 0,8 (п. 5.2 СП 64.13330.2011); mп – коэффициент перехода на породу дерева, для клена равен 1,3 (таблица 5 СП 64.13330.2011); mв – коэффициент, учитывающий условия эксплуатации (группу конструкций), равен 1,0 (таблица 7 СП 64.13330.2011); Rртабл – расчетное сопротивление древесины на растяжение, принимается по таблице 3 СП 64.13330.2011 и равно 7 МПа. Для вычисления Fнт выбираем самый опасный участок, где на расстоянии 200 мм имеет место наибольшая площадь ослаблений (не попадающих при перемещении вдоль волокон одно на другое). Такой участок будет на участке с отверстиями 4, 5 и 6. Согласно п. 6.1 совмещаем сечения 4, 5 и 6 в одно сечение. Fнт = Fбр – Fослаб = bh – 3db = 12•30 – 3•1,6•12 = 302,4 см2. Несущая способность растянутого элемента: N = 0,8•1,3•1,0•70•0,0302 = 0,21986 мН = 219,86 кН. Вывод: несущая способность деревянного элемента равна 219,86 кН. 2. Расчет центрально-растянутого элемента по первой группе предельных состояний проводим по формуле: 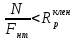 , ,где N – расчетная продольная сила, равна 70 кН; Fнт = 302,4 см2 (см. предыдущий пример); 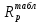 – расчетное сопротивление древесины на растяжение, принимается по таблице 3 СП 64.13330.2011 и равно 7 МПа; – расчетное сопротивление древесины на растяжение, принимается по таблице 3 СП 64.13330.2011 и равно 7 МПа;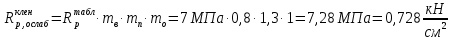 . .Проверяем условие: 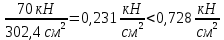 Вывод: условие выполнено, следовательно, элемент удовлетворяет условию прочности. И 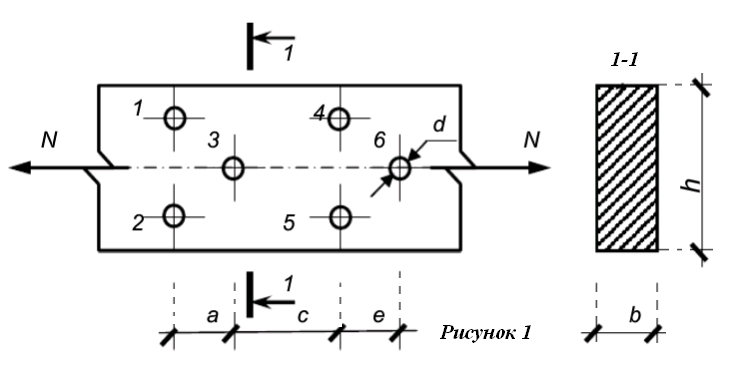 сходные данные к задаче 1.1
Варианты к задаче 1.1 студенты выбирают по следующим правилам: По первой букве фамилии студента выбираются параметры:
По первой букве имени студента выбираются параметры:
Задача 1.2 Расчет центрально-сжатых элементов (расчет на сжатие) Определить несущую способность центрально-сжатого деревянного элемента (рисунок 2) сечением bxh, ослабленного двумя отверстиями, выходящими на пласть, диаметром d с исходными данными согласно варианту. Пример выполнения задачи 1.2 Определить несущую способность центрально-сжатого деревянного элемента (рисунок 2) сечением bx h, ослабленного двуми отверстиями, выходящими на пласть, диаметром d с исходными данными: h = 20 см; b = 12,5 см; а = 15 см; ℓ = 3,0 м; d = 4 см; условия закрепленияконцов стержня в плоскостях Х – Х и У – У: шарнирное (Ш – Ш); материал элемента: береза; условия эксплуатации: 2; сорт древесины: 2. Решение 1. Несущая способность центрально-сжатого стержня с учетом устойчивости подсчитывается по формуле: 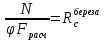 Для этого определим сначала расчетное сопротивление березы: 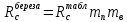 , ,где mп – коэффициент перехода на породу дерева, для березы равен 1,1 (таблица 5 СП 64.13330.2011); mв –коэффициент, учитывающий условия эксплуатации (группу конструкций), равен 0,9 (таблица 1,7, Приложение Г СП 64.13330.2011); Rртабл – расчетное сопротивление древесины, принимается по таблице 3 СП 64.13330.2011 и равно 7 МПа. Следовательно, 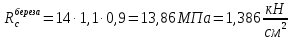 Для вычисления Fослаб участки ослабления принимаем совмещенными, т. к. расстояние между ними меньше 200 мм. 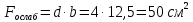 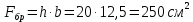 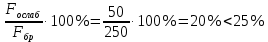 Следовательно, Fрасч = Fбр = 250 см2 (см. п. 6.2 СП 64.13330.2011). Для определения φ – коэффициента продольного изгиба – необходимо сначала определить гибкость элемента. Гибкость элементов цельного сечения определяют по формуле: 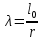 , ,где l0 – расчетная длина элемента; r – радиус инерции сечения элемента с максимальными размерами брутто относительно осей Х и У. Расчетную длину элемента l0 следует определять умножением его свободной длины l на коэффициент μ0: 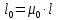 . .Согласно п. 6.23 СП 64.13330.2011 для шарнирного опирания 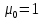 . .Отсюда 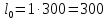 . .Радиус инерции сечения элемента с максимальными размерами определятся из формул: 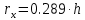 ; ;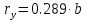 . .Максимальная гибкость элемента будет в плоскости Y – Y, следовательно 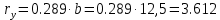 . .Значит, 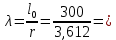 83,04. 83,04.Так как 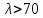 , где коэффициент А = 3000 для древесины, то согласно п. 6.3 СП 64.13330.2011 , где коэффициент А = 3000 для древесины, то согласно п. 6.3 СП 64.13330.2011 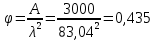 . .Несущая способность сжатого элемента: 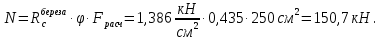 2. Несущая способность центрально-сжатого стержня с учетом прочности подсчитывается по формуле: 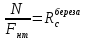 ( (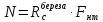 ), ),где 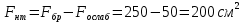 . .Следовательно, 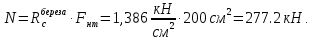 Вывод: Несущая способность центрально-сжатого деревянного элемента 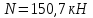 (выбирается минимальная несущая способность элемента). (выбирается минимальная несущая способность элемента).И 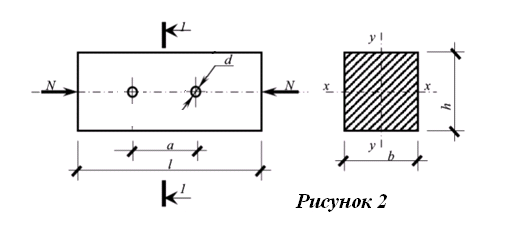 сходные данные к задаче 1.2
* Примечание: ш – шарнирное закрепление; з – защемление; о – свободное, без закреплений Варианты к задаче 1.2 студенты выбирают по следующим правилам: По первой букве фамилии студента выбираются параметры:
По первой букве имени студента выбираются параметры:
Задача 1.3 Расчет деревянных элементов, подверженных поперечному изгибу (расчет на изгиб) Подобрать сечение прямоугольной деревянной брусчатой шарнирно опертой балки (рисунок 3), нагруженной равномерно распределенной нагрузкой с исходными данными согласно варианту. Сечение подобрать из условия прочности по нормальным напряжениям и проверить на прочность по касательным напряжениям (на скалывание). Сечение подобрать из условия 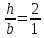 . .Пример выполнения задачи 1.3 Подобрать сечение прямоугольной деревянной брусчатой шарнирно опертой балки (рисунок 3), длиной 5 м, нагруженной равномерно распределенной нагрузкой q = 6 кН/м, порода балки – береза, класс эксплуатации – А1, сорт древесины – 2. Сечение подобрать из условия прочности по нормальным напряжениям и проверить на прочность по касательным напряжениям (на скалывание). Сечение подобрать из условия 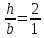 . .Р 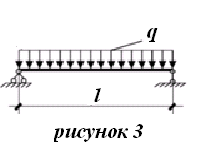 ешение П 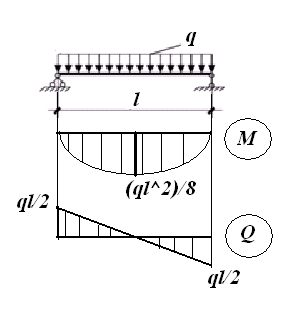 редварительно определим внутренние усилия и геометрические характеристики сечения. Для определения усилий построим эпюры внутренних усилий. редварительно определим внутренние усилия и геометрические характеристики сечения. Для определения усилий построим эпюры внутренних усилий.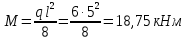 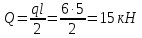 Далее определим геометрические характеристики сечения. 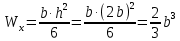 Определим расчетное сопротивление: 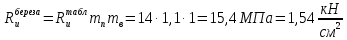 , ,где mп – коэффициент перехода на породу дерева, для березы равен 1,1 (таблица 5 СП 64.13330.2011); mв – коэффициент, учитывающий условия эксплуатации (группу конструкций), равен 1 (таблица 1,7 Приложения Г СП 64.13330.2011); Rитабл – расчетное сопротивление древесины, принимается по таблице 3 СП 64.13330.2011 и равно 14 МПа. 1. Прочность по нормальным напряжениям проверяется по формуле: 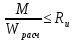 Из этого условия найдем величину b: 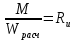 , ,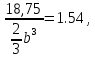 получаем получаем 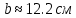 . .Примем b = 12.5 см, следовательно, h = 25 см. Выполним проверку подобранного сечения 12,5 х 25 на прочность по нормальным напряжениям: 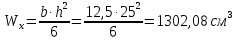 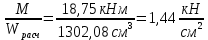 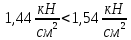 Условие выполняется, значит, прочность по нормальным напряжениям обеспечена. 2. Проверим подобранное сечение на прочность по касательным напряжениям (на скалывание). Проверка выполняется по формуле: 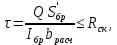 где Q – расчетная поперечная сила; S´бр – статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси; Iбр – момент инерции брутто поперечного сечения элемента относительно нейтральной оси; bрас – расчетная ширина сечения элемента; Rск – расчетное сопротивление скалыванию при изгибе. 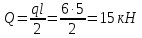 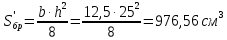 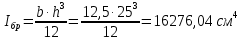 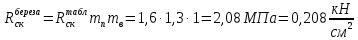 , ,где mп – коэффициент перехода на породу дерева, для березы равен 1,3 (таблица 5 СП 64.13330.2011); mв – коэффициент, учитывающий условия эксплуатации (группу конструкций), равен 1 (таблица 1,7 Приложения Г СП 64.13330.2011); Rсктабл – расчетное сопротивление древесины, принимается по таблице 3 СП 64.13330.2011 и равно 1,6 МПа. 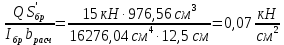 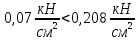 Условие выполнено, следовательно, прочность по касательным напряжениям обеспечена. Вывод: подобрано сечение прямоугольной деревянной брусчатой шарнирно опертой балки размером 12,5 см на 25 см, которое удовлетворяет условию прочности по нормальным и касательным напряжениям. Исходные данные к задаче 1.3 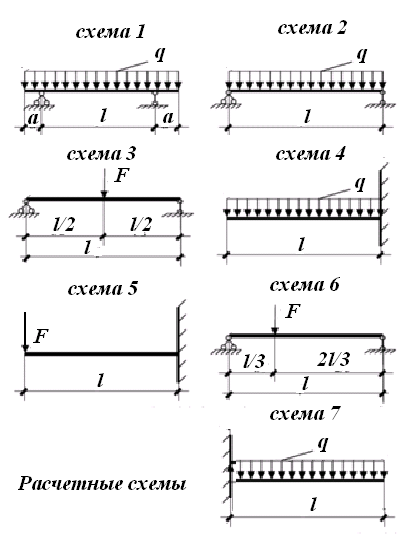
Варианты к задаче 1.3 студенты выбирают по следующим правилам: По первой букве фамилии студента выбираются параметры:
По первой букве имени студента выбираются параметры:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
