Перевод статей(Сницерук Павел). Расчет дифракции шести пучков в слоистых средах с использованием полиномов основных миноров
 Скачать 353.73 Kb. Скачать 353.73 Kb.
|
|
2.3 Представление коэффициентов пересчета Распределение энергии падающей волны между волнами SH 1 , SV 1 , P 1 , SH 2 , SV 2 , P 2 характеризуем коэффициентами преобразования упругих волн C gh = ∣∣||чA 0 г ∣|||2 , g = 1, 2, 3, h = 1, ..., 6 (10) где обозначения A h определяются формулой (8). В частности, C 11 , C 22 и C 33 представляют коэффициенты отражения SH-, SV- и P-волн соответственно. Подстановка выражений (9) в формулу (5) дает систему алгебр уравнения Брейка относительно амплитуд A h , h = 1, ..., 6. Решение этой системы дает следующее представление для коэффициентов преобразования: C gh = ∣∣||Д чД ∣∣∣|2, D = ∣∣∣∣∣||д 11··· д 16.........д 61··· д 66|||||||, D h = ∣∣∣∣∣||··· d 1 (h − 1)f 1d 1 (h + 1) ..................··· d 6 (ч − 1)f 6д 6 (ч + 1) ...|||||||, (11) где h = 1, ..., 6; определители D, D h состоят из элементов dgl = {6ΣJ = 1t gj b jl , если l = 1, 2, 3,−b gl ,если l = 4, 5, 6,f g = -6ΣJ = 1t gj b j0 , g = 1, ..., 6, (12) и t gj являются элементами матрицы переноса (6). Методика расчета матрицы переноса рассматривается в следующем разделе. Методика расчета Основное свойство экспоненциальной функции позволяет нам представлять матрицу (6) следующим образом: T = [exp (W d / m)] m . Мы используем обозначения: W d / m ≡ V ≡ v gh , exp V ≡ A ≡ a gh . Передаточная матрица Т шестого порядка согласно [5, 6] можно рассчитать по формулам: T = A m , A =5Σл = 0V л (1 л! + ЛΣг = 0p 6 − l + g (v qr )6 + N,ΣJ = 6B j − 1 − g (v qr )J!). (13) Здесь p j (v qr ) обозначают коэффициенты характеристического уравнения для матрицы V. Полиномы B l (v qr ) определяются рекуррентными соотношениями [7]: B 0 (v qr ) = ... = B 4 (v qr ); B 5 (v qr ) = 1; B j (v qr ) =6ΣI = 1p i (v qr ) B j − i (v qr ). (14) Начинается процедура вычисления матрицы A согласно (13–14) от выбора параметра масштабирования m = 2 j и числа N (см. формулу (13)). Эти значения должны удовлетворять условиям [5]: m> n ≡ 8.5ωd√ρ макс S GH , ε м ≡ η N + 1м N (6 + N) ∏ Nч = 1 (6 + ч)<10 −3 . (15) Вторым из соотношений (15) является оценка ошибки усечения ϵ m в расчете на матрицу Т по формулам (13). Это отражает тот факт, что погрешность измерений плотности ρ и тензорных составляющих S gh равна обычно больше 10 -3 . Расчеты матриц V 2 , ..., V 5 и коэффициентов p j являются формируется по методу Ле Верье [7]. Алгоритмы вычисления полиномов B j (v qr ), j = 6, ..., N + 5 и матрица A по уравнениям (14) и (13), соответственно действительно, очевидны. Наконец, передаточная матрица T = A 2 j находится по формуле: A 2 j= (... ((A) 2 ) 2 ...) 2 ,если j <6, (16) =н-1Σч = 0ччасΣг = 0p n − h + g (a qr ) B 2 j −1 − g (a qr ), если j ≥ 6, (17) где полиномы В J (а дг ) определяются уравнениями , подобными (14) (V дг являются заменено на qr ). Предложение 2. Пусть N 1 и N 2 - числа арифметических сложений и умножения, которые требуются для вычислений A 2 j по формулам (16) (j-кратный квадрат) и (17) соответственно. Существует алгоритм для вычисления A 2 jпо формуле (17), в которой N 2 Доказательство. Примером такого алгоритма для матриц второго порядка был представлен в [6]. Аналогичный подход для матриц шестого порядка дает N 1 / N 2 > 396j / (1563 + 122j). Таким образом, (17) более эффективно, чем (16), если j ≥ 6. 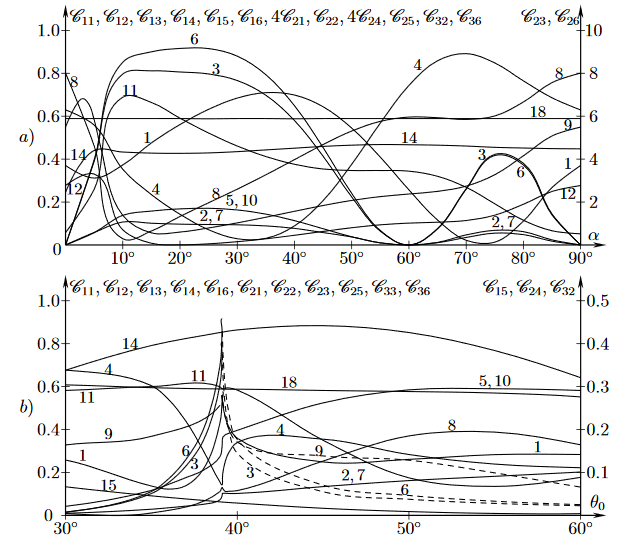 Рисунок 2. Коэффициенты преобразования: а) C gh (α), если θ 0 = 39,13 ◦ ; б) C gh (θ 0 ), если α = 20 ◦ Приведен пример результатов расчетов по формулам (11) - (17) на рис. 2. Здесь приведены зависимости коэффициентов пересчета C gh от углов падения для кристаллического слоя Si. Плоскость z = 0 совпадает с поверхностью кристалла (001). В кристалле Si ненулевые компоненты соответствия тензор согласно [3] имеет значения: S 11 = S 22 = S 33 = 7,69 · 10 -12 м 2 / Н, S 12 = S 13 = S 23 = -2,14 · 10 -12 м 2 / Н, S 44 = S 55 = S 66 = 12,58 · 10 -12 м 2 / Н. Значения ρ = 2.329 · 10 3 кг / м3, d = 10 −4 м, ω = 3π10 7 Гц, ρ 1 = ρ 2 =2,65 · 10 3 кг / м 3 , λ 1 = λ 2 = 1,67 · 10 10 Н / м 2 , μ 1 = μ 2 = 3,27 · 10 10 Н / м 2, имеют также был использован в расчетах. Функциональные кривые C 11 (θ 0 , α), C 12 (θ 0 , α), C 13 (θ 0 , α), C 14 (θ 0 , α), C 15 (θ 0 , α), C 16 (θ 0 , α), C 21 (θ 0 , α), C 22 (θ 0 , α), C 23 (θ 0 , α), C 24 (θ 0 , α), C 25 (θ 0 , α), C 26 (θ 0 , α), C 31 (θ 0 , α), C 32 (θ 0 , α), C 33 (θ 0 , α), C 34 (θ 0 , α), C 35 ( 0 , α), C 36 ( 0 , α) имеют номера 1, 2, ..., 18. соответственно. Значения C 26 (θ 0 , α = 20), C 31 , C 34 , C 35 не показаны, поскольку они значительно меньше чем другие коэффициенты C гч . Амплитуда рассеянной волны A j может быть больше, чем амплитуда падающая волна A 0 (см., например, кривые 9 и 12 на рис. 2а). Это согласно с законом сохранения потока энергии v 0 cosθ 0 = (C g1 + C g2 ) v S 1 cos θ S 1 + (C g4 + C g5 ) v S 2 cos θ S 2 +2ΣJ = 1C g (3 × j) v P j cos θ P j . Если падающая волна имеет тип SH или SV, амплитуды продольных волн иметь максимальные значения при критических углах падения, которые определены по условиям sin θ 0 C= k P j / k 0 , j = 1, 2. В рассматриваемом случае они равны θ 0 C = 39,13 ◦ . Если θ 0 > θ 0 C , то распространяются неоднородные плоские продольные волны вдоль интерфейсов z = 0 (в области z <0) и z = d (в области z> d). Зависимости C 13 (θ 0 ), C 16 (θ 0 ), C 23 (θ 0 ) для этих неоднородных волн имеют вид показано на рис. 2б пунктирными линиями. В заключение отметим, что метод расчета коэффициентов пересчета не требует нахождения кинематических характеристик волн в анизотропный слой. Это упрощает расчеты и делает их более надежными. Список литературы [1] WM Ewing, WS Jardetzky, F. Press, Упругие волны в слоистых средах, McGraw-Hill Book Company, Нью-Йорк, 1957. [2] К. Ари, П. Г. Ричардс, Количественная сейсмология, Университетские научные книги, Саусалито, 2002. [3] E. Dieulesaint, D. Royer, Ondes ´Elastiques Dans Les Solides, приложение au traitment du signal, Masson, Paris, 1974. [4] Л.М. Бреховских, О.А. Годин, Акустика слоистых сред I, Springer- Верлаг, Берлин, 1990. http://dx.doi.org/10.1007/978-3-642-52369-4 [5] Ю.Н. Беляев, Передаточная матрица шестого порядка, Учеб. Int. Conf. Дней по дифракции, (2014), 37 - 42. http://dx.doi.org/10.1109/DD.2014.7036420 [6] Ю.Н. Беляев, Рекуррентные соотношения между симметрическими полиномами n-го порядка, Прикладные математические науки, 8 (2014), 5195 - 5202. http://dx.doi.org/10.12988/ams.2014.47525 [7] Ю.Н. Беляев, О вычислении функций матриц, Математика Notes, 94 (2013), 177 - 184. Ссылка на статью: http://www.m-hikari.com/ams/ams-2015/ams-109-112-2015/p/belyayevAMS109-112-2015.pdf |
