39_Архангельск ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. Расчёт электрического поля, усилий, энергии и электрических параметров простейших конструкций
 Скачать 445.57 Kb. Скачать 445.57 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования «Северный (Арктический) федеральный университет имени М.В. Ломоносова» ________________________ВШЭНиГ_____________________________ (наименование высшей школы / филиала / института / колледжа) КОНТРОЛЬНАЯ РАБОТА №1
Архангельск 2019 СОДЕРЖАНИЕ
1 РАСЧЁТ ЭЛЕКТРИЧЕСКОГО ПОЛЯ, УСИЛИЙ, ЭНЕРГИИ И ЭЛЕКТРИЧЕСКИХ ПАРАМЕТРОВ ПРОСТЕЙШИХ КОНСТРУКЦИЙ 1.1Цель задания Целью задания является закрепление теоретического материала, излагаемого в первой части курса – физические основы электротехники (ФОЭ). Теоретическая часть расчётов базируется на уравнениях поля в интегральной форме. Особенности конструкций элементов (сферическая и цилиндрическая симметрия) существенно упрощают расчётную часть и позволяют при выполнении задания сосредоточить внимание на физической стороне процессов. 1.2 Содержание задания В соответствие с буквенной литерой (А, m – 1, n – 3) выбирается расчётный вариант, заданный геометрией элемента, номерами условий задания и номерами самого задания в соответствии с таблицей 1 Таблица 1  2 ЗАДАНИЕ №1 Найти зависимости электрического смещения D, напряжённости электрического поля Е, поляризованности Р и потенциала U в произвольной точке как функции расстояния r (d). Начало отсчёта (r или d = 0) считать в центре сфер или на оси цилиндрических поверхностей (в плоском конденсаторе от верхней пластины). Построить графики зависимостей  ; ;  ; ;  ; ;  и объяснить характер их изменений во всех областях и на границах этих областей. и объяснить характер их изменений во всех областях и на границах этих областей.Найти выражения объёмной плотности энергии электрического поля 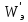 во всех областях. Построить график во всех областях. Построить график 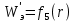 . .Решение По объему проводящего заряженного шара однородно распределен заряд q. Внутри проводящего шара (область 1) поле отсутствует. Найдём зависимость электрического смещения  . Основа для расчёта – постулат Максвелла: . Основа для расчёта – постулат Максвелла: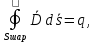 (1.1) (1.1)где  - объемная плотность заряда, - объемная плотность заряда, V – объем заряженного проводящего шара. В силу симметрии поля смещение и напряженность на поверхности нулю, т.е.  , ,тогда 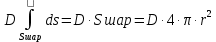 Тогда из вышеприведенного постулата Максвелла получим: 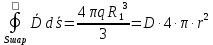 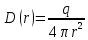 Это выражение справедливо в пределах от 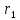 до бесконечности. Так как область 2 и область 3 – диэлектрики. до бесконечности. Так как область 2 и область 3 – диэлектрики.Напряжённость электрического поля найдём из соотношения.  (1.2) (1.2)Вектор 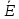 также совпадает с направление также совпадает с направление  . .Поляризованность диэлектрика в области 2 и в области 3 можно определить на основе выражения (1.3): 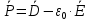  Окончательно: 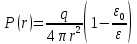 (1.3) (1.3)Для определения потенциала электрического поля воспользуемся выражением, принимая потенциал внутри заряженного шара равным нулю. Поскольку вектор 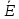 совпадает по направлению с совпадает по направлению с  , выражение перепишем в виде , выражение перепишем в виде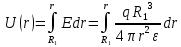 (1.4) (1.4)Путь интегрирования от R1 до произвольной точки r проходит в областях с различной диэлектрической проницаемостью, то при переходе из области 2 в область 3 подынтегральная функция меняется скачком. Поэтому при 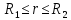  При 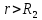 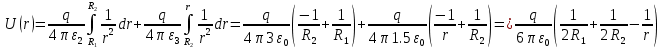 Для построения графиков подставим известные постоянные значения. Из условия задачи найдем    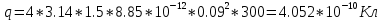 Определим объёмную плотность энергии электрического поля.  (1.5) (1.5)Таблица 2
Таблица 3
Ниже изображены графики – эпюры полученных зависимостей с указанием номера области. На графике объёмной плотности энергии видно, что при переходе из области 2 в область 3 происходит скачёк, что объясняется скачкообразным изменением свойств среды на границе двух диэлектриков. 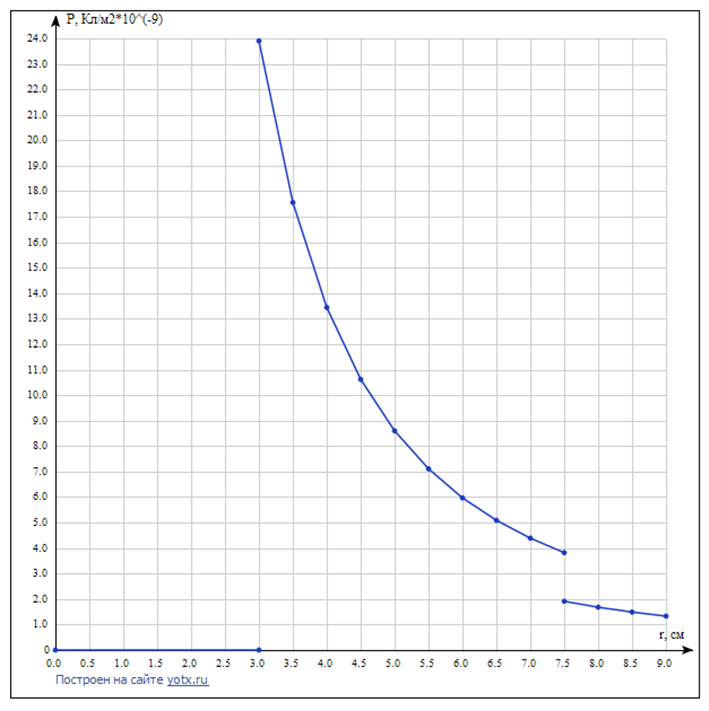   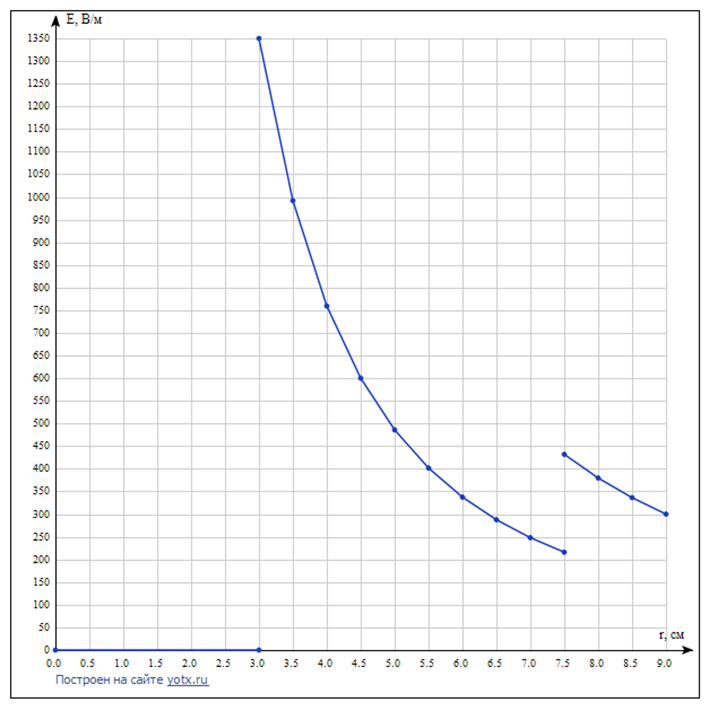 3 ЗАДАНИЕ №4 В области 2 определить полную энергию электрического поля для сферических конструкций и энергию электрического поля на единицу длины для плоских и цилиндрических конструкций. Для m=1 найти потенциал заряженного тела относительно бесконечно удалённой точки. Условия задания: В точке с координатой 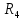 (или (или  ) напряжённость электрического поля равна ) напряжённость электрического поля равна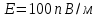 . .1 – проводящий шар радиусом  ; ;2 – оболочка из диэлектрика с внешним радиусом  , и диэлектрической проницаемостью , и диэлектрической проницаемостью 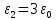 ; ;3 – окружающее пространство – диэлектрик с диэлектрической проницаемостью  при m нечётном и при m нечётном и 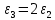 при m чётном; при m чётном;R4 – точка с координатой 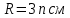 . .При m=1 и n=3 имеем:  ; ; ; ; ; ;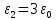 ; ;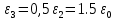 ; ; . . . .Конструкция 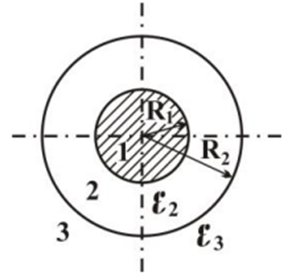 Решение Предусмотрен расчет энергии электрического поля в области 2.   = = Для m=1 найти потенциал заряженного тела относительно бесконечно удалённой точки. Для заряженного шара потенциал равен: Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы и равны потенциалу на поверхности шара. 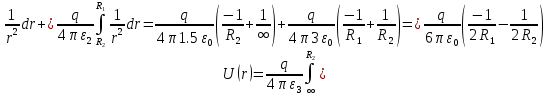  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||