G1N4 Закиров Тагир зэмк1-18. Расчет и моделирование регулирующего аппарата
 Скачать 112.52 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский государственный энергетический университет» КОНТРОЛЬНАЯ РАБОТА по дисциплине «Электрические и электронные аппараты» Тема: Расчет и моделирование регулирующего аппарата Выполнил: Закиров Т.И. Группа: зЭМК-1-18 Проверил: Варенов А.А. Казань 2023 Оценка устойчивости САР частоты синхронного генератора Определить передаточную функцию разомкнутой системы, используя ССДМ (рисунок 1); найти выражение характеристического уравнения замкнутой системы по формуле А(s)= В(s)+ D(s) = 0; определить численные значения коэффициентов а3, а2, а1, а0 этого уравнения, используя значения исходных параметров системы; оценить устойчивость САР по критерию Гурвица и определить критическое значение коэффициента передачи Ккр, при котором система находится на границе устойчивости. 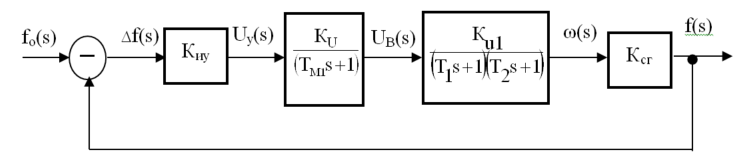 Рис.1.ССДМ системы стабилизации частоты б). Решение задачи. - определение передаточной функции разомкнутой САР 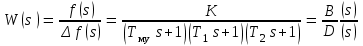 - расчет параметров передаточной функции по исходным параметрам системы, которые определяются каждым студентом по своему варианту: Значения исходных параметров: Постоянные параметры
Варьируемые параметры:
Варьируемые параметры вычисляются в зависимости от номера группы G и номера в журнальном списке N 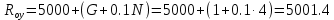 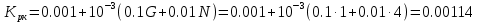 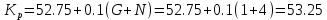 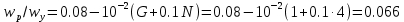 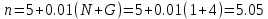 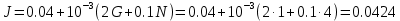 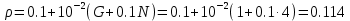 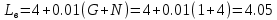 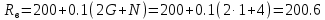 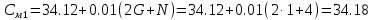 Значения параметров передаточных функций 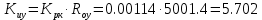 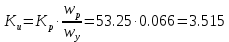 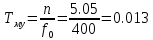 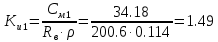 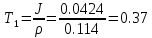 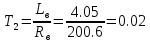 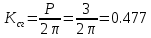 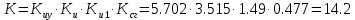 - нахождение выражения характеристического уравнения замкнутой САР А(s) = В(s) + D(s) = (Тму s+1) (Т1 s+1) (Т2 s+1) + К =  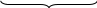 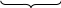 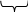 = Тму Т1 Т2 s3 +( Тму Т1+ Т1 Т2+ Т2 Тму) s2 +( Тму + Т1 +Т2) s + 1 + К = 0.а3 а2 а1 а0 - определение численных значений коэффициентов этого уравнения 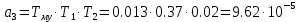 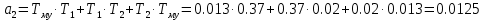 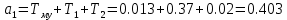 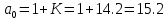 - оценка устойчивости САР по критерию Гурвица а3 > 0; а2 > 0; а1 > 0; а1 > 0 – необходим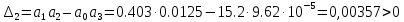ое условие устойчивости;  – достаточное условие устойчивости.Вывод: Система в замкнутом состоянии устойчива. - определение значения Kкр. Из условия 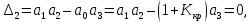 при выполнении которого система находится на границе колебательной устойчивости, выразим Kкр 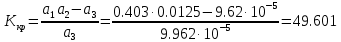 3.2. Разработка схемы моделирования системы стабилизации частоты синхронного генератора в cреде MatLab Целью компьютерного моделирования является получение временных и частотных характеристик, по которым судят об устойчивости и показателях качества систем. Одним из пакетов программ компьютерного моделирования является система MatLab (матричная лаборатория) и ее основной пакет расширения Simulink. Запись уравнений в программе Simulink можно осуществить в виде схемы моделирования, что очень удобно. Схема моделирования, построенная в программе MatLab, представлена на рис.2. 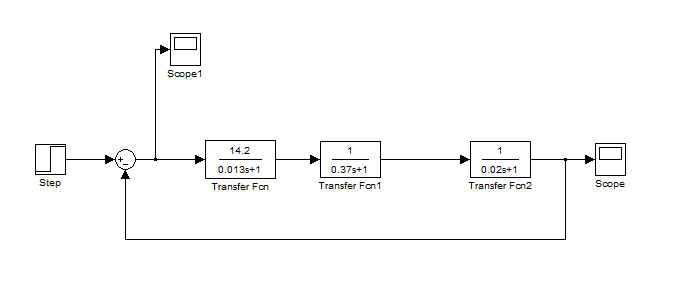 Рис. 2 Схема моделирования ССЧ с числовыми значениями в среде MatLab Переходная характеристика для данного варианта решения задачи показана на рис. 3. 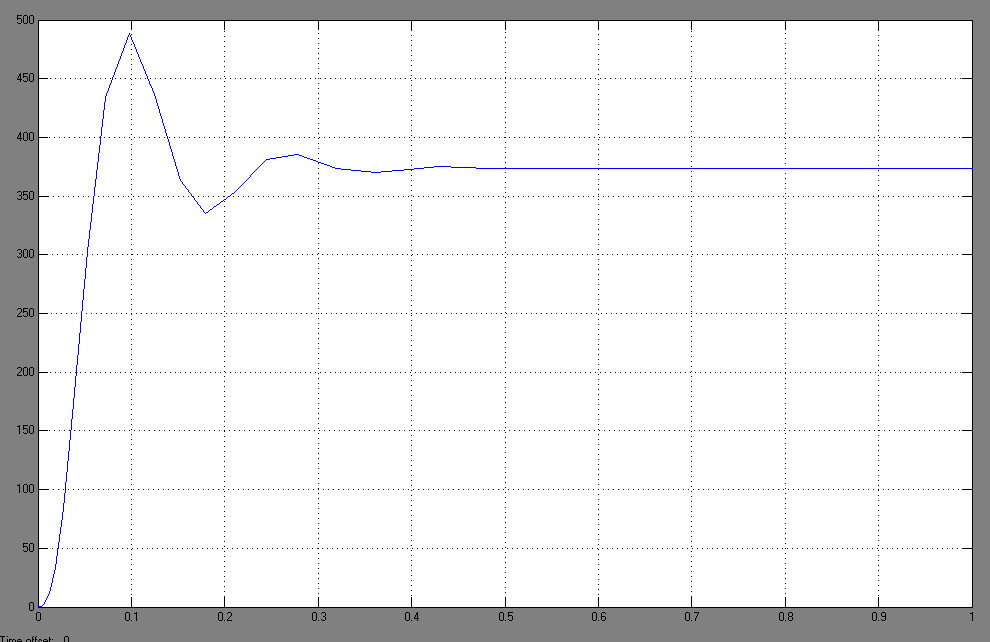 Рис. 3 Переходная характеристика ССЧ По переходной характеристике определяем прямые показатели качества системы: время регулирования tр=0,45 секунды и величину перерегулирования: 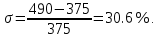 Построение логарифмических частотных характеристик >> num1=[14.2]; >> den1=[0.013 1]; >> sys1=tf(num1,den1) sys1 = 14.2 ----------- 0.013 s + 1 Continuous-time transfer function. >> num2=[1]; >> den2=[0.37 1]; >> sys2=tf(num2,den2) sys2 = 1 ---------- 0.37 s + 1 Continuous-time transfer function. >> num3=[1]; >> den3=[0.02 1]; >> sys3=tf(num3,den3) sys3 = 1 ---------- 0.02 s + 1 Continuous-time transfer function. >> sys=sys1*sys2*sys3 sys = 14.2 --------------------------------------- 9.62e-05 s^3 + 0.01247 s^2 + 0.403 s + 1 Continuous-time transfer function. >> bode(sys) В результате введения этой программы на экране монитора появляется диаграмма Бодэ, показанная на рис. 4. 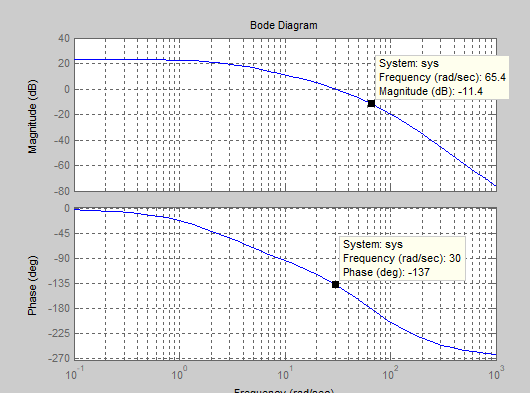 Рис. 4 Диаграмма Бодэ Cделаем вывод об устойчивости системы по критерию Найквиста: Построим диаграмму Найквиста с помощью следующей команды: >> nyquist(sys) На рис.5 представлена диаграмма Найквиста. Поскольку АФЧХ разомкнутой системы не охватывает точку с координатами (-1, j0), то, согласно критерию Найквиста САУ с заданными параметрами является устойчивой. Определим запасы устойчивости по фазе и амплитуде. Как видим по рис.4, запас устойчивости по амплитуде равен 11,4 Дб (Gain Margin=11.4dB), а по фазе 43º (Phase Margin=43 deg). 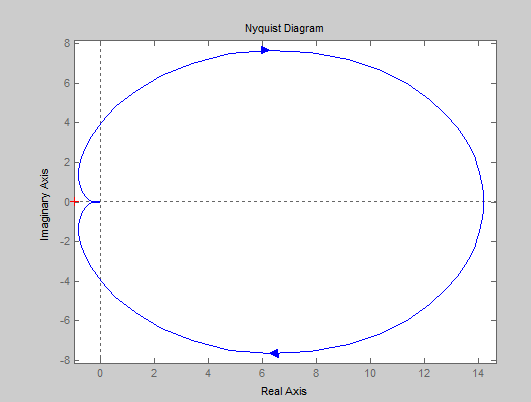 Рис.5 Диаграмма Найквиста Литература Электрические и электронные аппараты: Учебник / Под ред. проф. Варенова А.А., МО РФ,2009, 448с. Солодовников В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем автоматического регулирования. М.: Машиностроение, 1985. |