РАСЧЕТ КОЭФФИЦИЕНТОВ АВТОКОРРЕЛЯЦИИ. Отчет по практической работе(26).НечаевА.Г.БИ-б-о-181.. Расчет коэффициентов автокорреляции

• Название: Расчет коэффициентов автокорреляции
• Анкор: РАСЧЕТ КОЭФФИЦИЕНТОВ АВТОКОРРЕЛЯЦИИ
• Дата: 06.02.2023
• Размер: 235.35 Kb.
• Имя файла: Отчет по практической работе(26).НечаевА.Г.БИ-б-о-181..docx
• Тип: Практическая работа; #923330

ПРАКТИЧЕСКАЯ РАБОТА №26

Нечаев А.Г. БИ-б-о-181

ТЕМА: РАСЧЕТ КОЭФФИЦИЕНТОВ АВТОКОРРЕЛЯЦИИ

Цель: научиться рассчитывать автокорреляционную функцию

временного ряда.

Ход работы.

1. Постановка задачи.

Исходные данные о Величина прожиточного минимума по Республике Крым для всех групп населения (без деления по социально-демографическим группам ) представлены в таблице 1.

Таблица 1
Величина прожиточного минимума по Республике Крым

Год	Квартал №
	1	2	3	4
2016	9717	9794	9696	9502
2017	9542	9936	9803	9126
2018	9289	9808	9904	9814
2019	10309	10748	10509	10258

В ходе выполнения работы необходимо:

1. Построить поле корреляции временного ряда.

2. Рассчитать коэффициенты автокорреляции 1-4 порядка, объяснить их смысл, сопоставить со шкалой Чеддока.

3. Построить коррелограмму, сделать выводы.

4. Оценить на уровне значимости α =0,05

значимость коэффициента автокорреляции первого порядка, используя t – распределение

Стьюдента.

5. Найти коэффициент детерминации и объяснить его смысл.

Решение:

1. Построение поля корреляции временного ряда.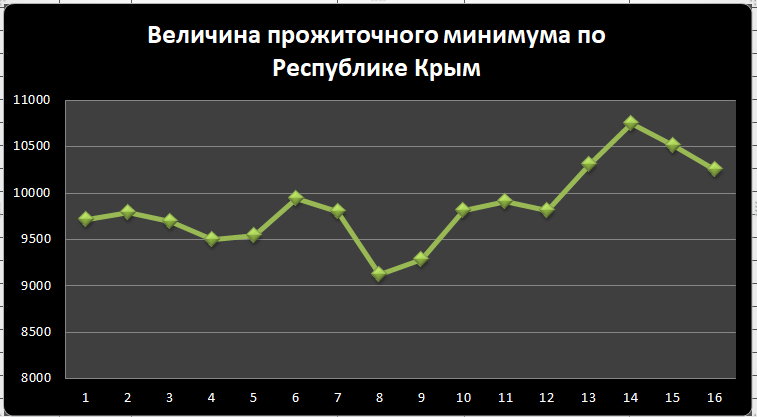



Рис.1. Корреляционное поле

2. Расчет коэффициента автокорреляции первого порядка.

Определим среднее значение: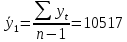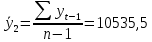





Для дальнейших вычислений построим расчётную таблицу (Рис.2)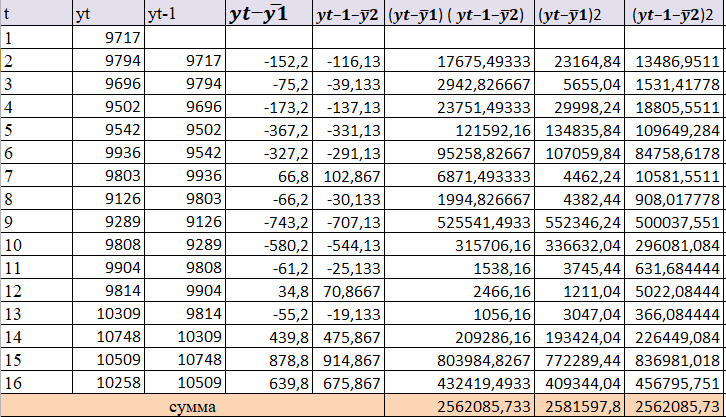



Рис.2. Расчетная таблица для 1 коэффициента автокорреляции

С помощью итоговых сумм рассчитаем величину коэффициента автокорреляции первого порядка: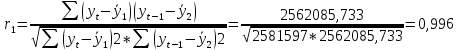



Рассчитаем коэффициент автокорреляции 2-го порядка.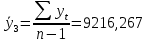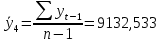





Расчетная таблица для коэффициента второго порядка представлена на рис.3.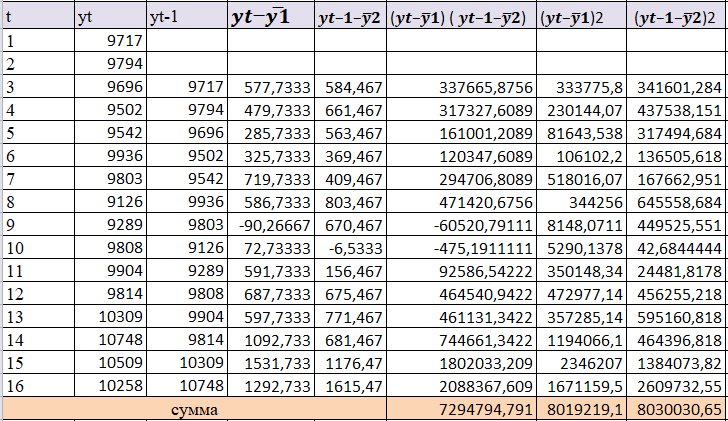



Рис.3. Расчетная таблица для 2 коэффициента автокорреляции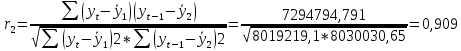



Рассчитаем коэффициент автокорреляции 3-го порядка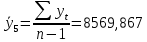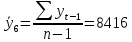





Расчетная таблица для коэффициента третьего порядка представлена на рис.4.



Рис.4. Расчетная таблица для 3 коэффициента автокорреляции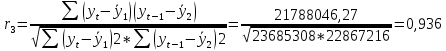



Рассчитаем коэффициент автокорреляции 4-го порядка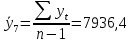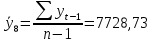





Расчетная таблица для коэффициента четвертого порядка представлена на рис.5.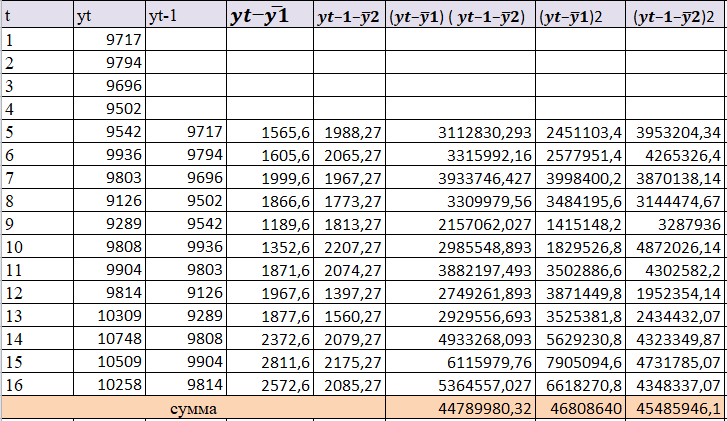



Рис.5. Расчетная таблица для 4 коэффициента автокорреляции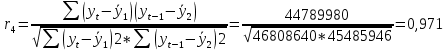



Сопоставим рассчитанные коэффициенты автокорреляции 1-4 порядка со шкалой Чеддока в Таблице 2.

Таблица 2. Коэффициенты автокорреляции

Порядок	1	2	3	4
Величина коэффициента	0,996	0,909	0,936	0,971
Сила связи	Очень высокая	Высокая	Высокая	Очень высокая

3. Построение коррелограммы и выводы о наличии тенденции, циклических колебаний.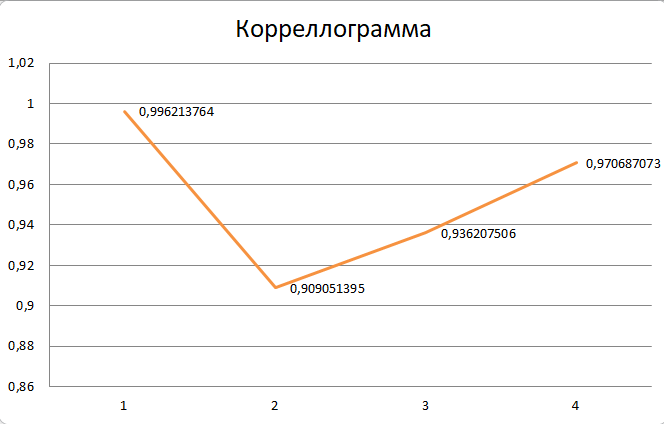



Рис.6. Коррелограмма

Из таблицы со значениями коэффициентов автокорреляции 1-4 порядка и коррелограммы видно, что, что наиболее высокий коэффициент автокорреляции наблюдается при значении лага, равном один, следовательно, наблюдаемый ряд имеет циклические колебания периодичностью в 1 квартал.

4. Оценим на уровне значимости α = 0,05 значимость коэффициент автокорреляции первого порядка используя t – распределение Стьюдента.

Для этого рассчитаем величину t_набл. для коэффициента корреляции первого порядка: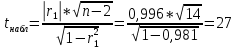



Найдем табличное значение t-критерия Стьюдента на уровне значимости   0,05 при числе степеней свободы n-2. По таблице t распределения Стьюдента: t_табл  t 1;n2  t 0,95;162  1,761.

Так как t_набл. > t_табл., то можно сделать вывод о значимости коэффициента корреляции первого порядка.

5. Найдем коэффициент детерминации.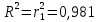



Полученное значение 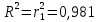говорит о том, что вариация значений временного ряда на 98% объясняется предыдущими значениями этого временного ряда.