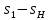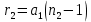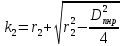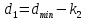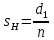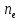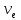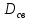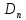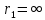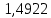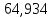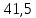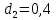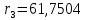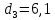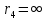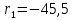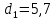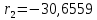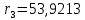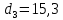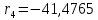Конденсоры. "Расчет конденсорных систем"
 Скачать 211.71 Kb. Скачать 211.71 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ Государственное бюджетное образовательное учреждение Российской Федерации Московский государственный университет геодезии и картографии Кафедра прикладной оптики Расчётно-графическая работа На тему: “Расчет конденсорных систем” Выполнил студент: Петров Владимир Александрович Направление специальности: ФОИСТ ЛТ и ЛТ 3-1б Научный руководитель: Запрягаева Л.А. Москва 2019 г. Расчёт осветительной системы, состоящей из двух плосковыпуклых линз с параллельным ходом лучей между ними. Исходные данные: Марка стекл – ЛК4 S1 = -45,5 β = -2,3 2 σохв = 49º n = 1,4922  Рисунок 1 - Схема конденсора, состоящего из двух плосковыпуклых линз 1.1 Габаритный расчет Рассчитаем диаметр первой линзы: 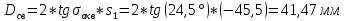 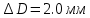 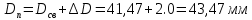 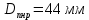 Методом последовательного приближения найдем 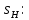 Найдем отрезок 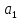 , задавшись , задавшись 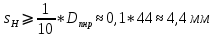 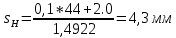
В результате расчета: 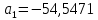 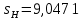 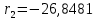 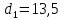 Определим конструктивные параметры линзы Для получения параллельности пучка лучей между линзами, необходимо выполнение условия: 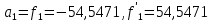 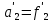 Тогда из уравнения увеличения в параксиальной области: 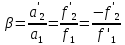 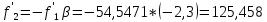 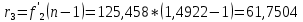 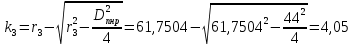 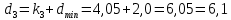 Конструктивные параметры:
1.2 Аберрационный анализ в области аберраций III-го порядка Определение продольной сферической аберрации: Продольная сферическая аберрация определяется суммированием аберраций 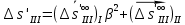 , ,где 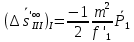 - продольная сферическая аберрация первой линзы в обратном ходе лучей. - продольная сферическая аберрация первой линзы в обратном ходе лучей.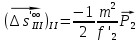 - продольная сферическая аберрация второй линзы в прямом ходе лучей. - продольная сферическая аберрация второй линзы в прямом ходе лучей.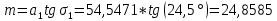 ; ;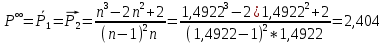 ; ;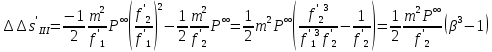 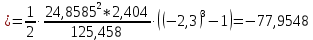 ; ;Определение поперечной сферической аберрации: 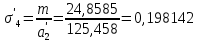 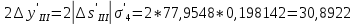 ; ;Кружок рассеяния в плоскости наименьшего кружка: 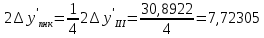 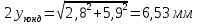 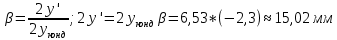 ; ;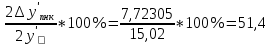 % %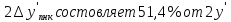 Определим эффективное увеличение оптической системы состоящей из двух бесконечно тонких плосковыпуклых линз в ПНК: 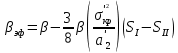 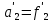 ; ;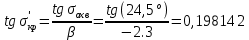  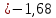 где для БТК: 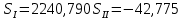 2 Расчет конденсорной системы из апланатического мениска и линзы, рассчитаной на минимум сферической аберрации. Исходные данные: 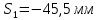 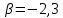 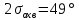 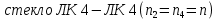 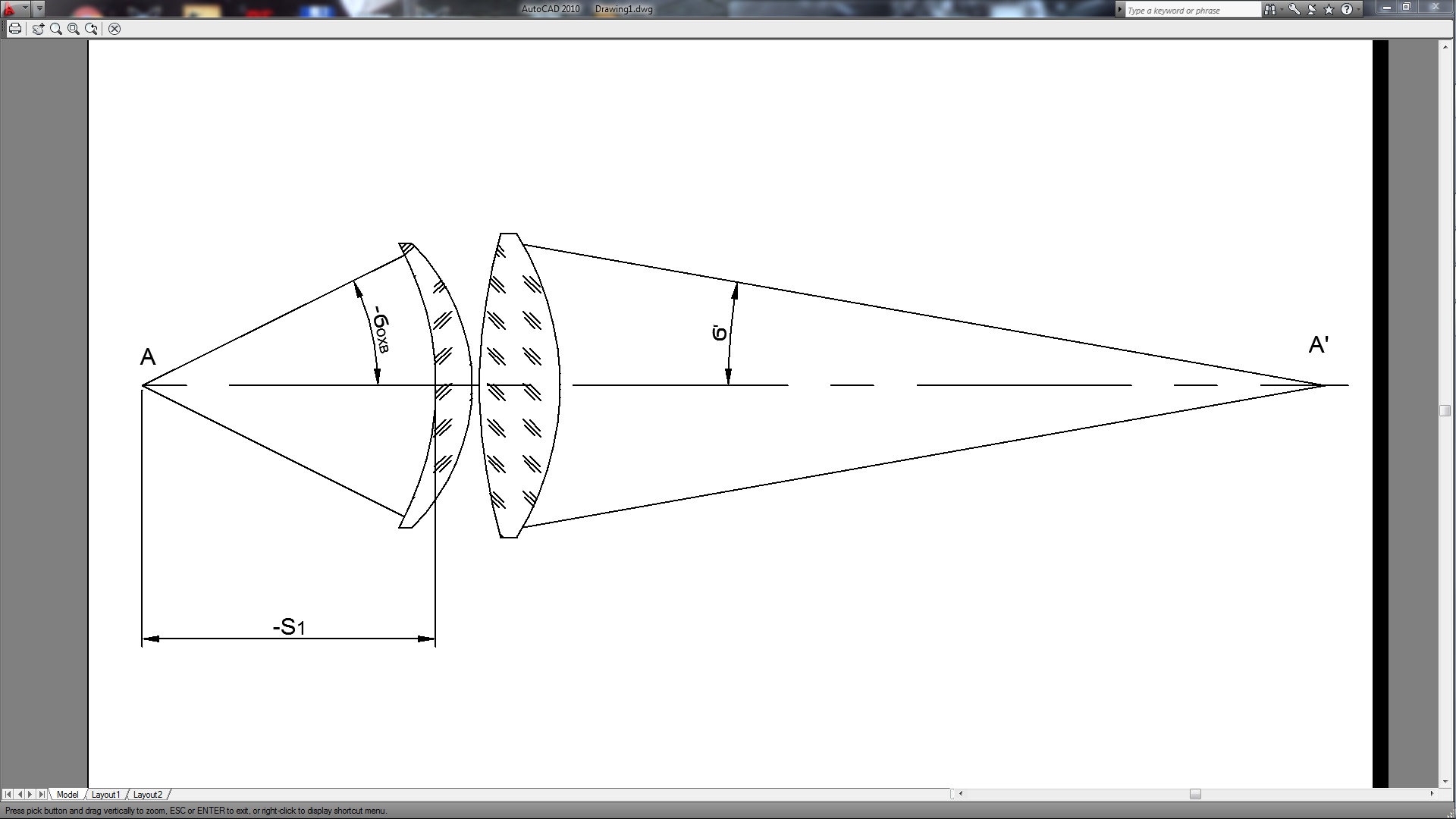 Рис. 1 - Схема конденсорной системы из апланатического мениска и линзы рассчитанной на минимум сферической аберрации 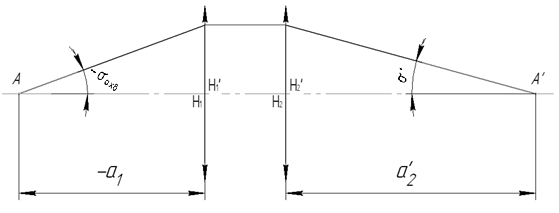 Рис. 2 - Схема конденсорной системы апланатического мениска и линзы на минимум сферической аберрации в тонких компонентах 2.1 Габаритный расчет Рассчитаем диаметр первой линзы: Найдем Dсв: 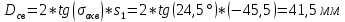 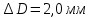 dmin=2,0 мм 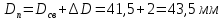 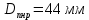 Найдем стрелки прогиба: 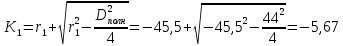 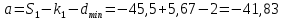 Условие определения радиуса: 1) 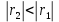 2) 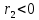 Запишем квадратное уравнение: 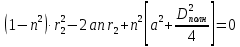 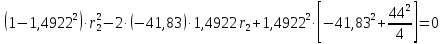 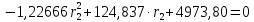 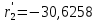 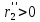 – не удовлетворяет условию – не удовлетворяет условиюНайдем стрелку прогиба: 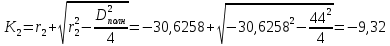 Найдем толщину линзы: 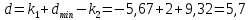 Уточняем значение r2: 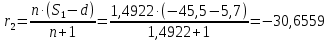 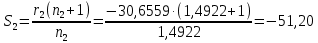 ; ;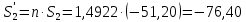 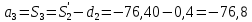 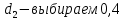 Конструктивные параметры апланатического мениска:
Расчет линзы на min сферической аберрации Если за первым апланатическим мениском стоит линза на минимум сферической аберрации выполняется нормировка 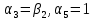 . Линза принимается бесконечно тонкой, при этом d3 = 0, h3 = h4 = h = a3α3 . Линза принимается бесконечно тонкой, при этом d3 = 0, h3 = h4 = h = a3α3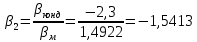 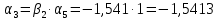 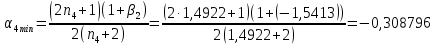 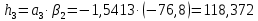 Радиусы кривизны для БТЛ: 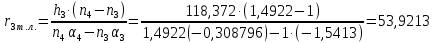 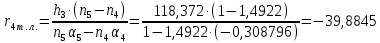 Переходим к линзе конечной толщины: 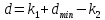 Найдем световой диаметр: Формула для перехода следующей за мениском линзы 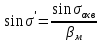 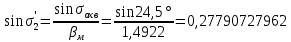 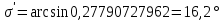 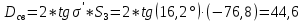 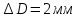 dmin=2 мм 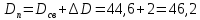 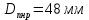 Определим стрелки прогиба: 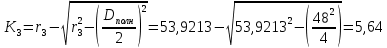 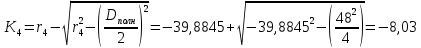 Для реальной системы: 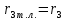 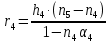 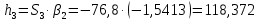 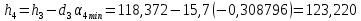 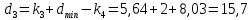 Пересчитаем 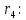 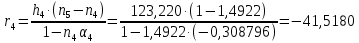 Пересчитаем стрелку прогиба: 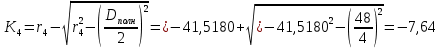 Пересчитаем толщину линзы 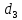 ; ;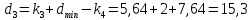 Пересчитаем 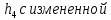 толщиной: толщиной: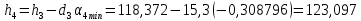 Уточняем 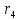 : :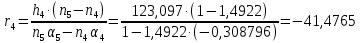 Конструктивные параметры:
Определение продольной и поперечной сферической аберрации 3го порядка 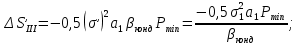 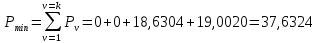 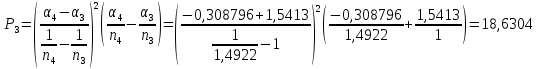 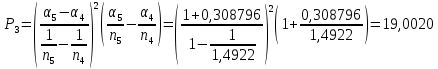 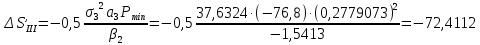 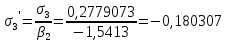 Поперечная сферическая аберрация: 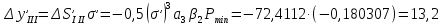 Кружок рассеяния: 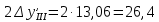 Кружок рассеяния в плоскости наименьшего кружка: 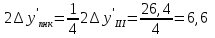 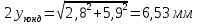 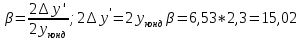 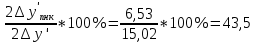 % %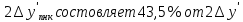 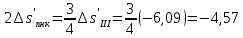 ; ; |