ргр губенко. ГУБЕНКО РГР. Расчет конструкции балочной клетки
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
Министерство науки и высшего образования Российской Федерации федеральное государственное автономное образовательное учреждение высшего образования «Северный (Арктический) федеральный университет имени М.В. Ломоносова» ВЫСШАЯ ИНЖЕНЕРНАЯ ШКОЛА РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
Архангельск 2021 ЛИСТ ДЛЯ ЗАМЕЧАНИЙ ЛИСТ ЗАДАНИЯ СОДЕРЖАНИЕ 1 Выбор схемы балочной клетки 1.1 Нормальная балочная клетка Нормальная балочная сетка (НБК) (рис. 1.1) состоит из колонн, на которые опираются сварные двутавровые главные балки, по которым, в свою очередь, устанавливаются прокатные балки настила. По балкам настила укладывается стальной настил. 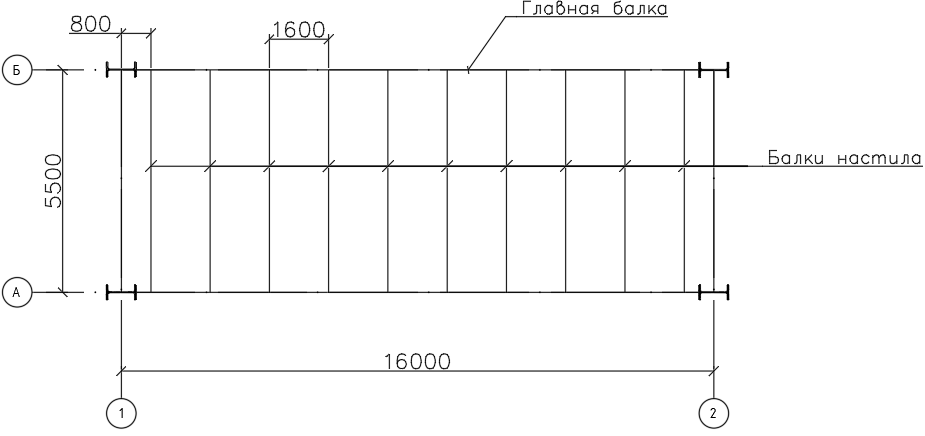 Рисунок 1.1 – Нормальная балочная клетка Шаг балок настила a = 0,6-1,6 м, при этом балка настила не ставится в середине ее пролета. Толщину стального настила определяем с учетом жесткости по формуле  , (1.1.1) , (1.1.1)где lн – пролет настила, м, для нормальной балочной клетки принимаем lн= 1,6 м; tн – толщина настила, м; n0 – величина, обратная предельной деформации, n0 = 200; E1 – приведенный модуль упругости стали с учетом поперечной деформации, E1 = 2,26⋅108 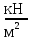 ; ;pn – временная нормативная нагрузка, pn = 28 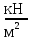 ; ; . .Толщина настила для нормальной балочной клетки 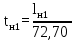 (1.1.2) (1.1.2) 0,0220 м = 22 мм 0,0220 м = 22 ммВ соответствии с ГОСТ 19903 – 74* принимаем tн1=22 мм. Расчетная схема балки настила приведена на рис. 1.2. 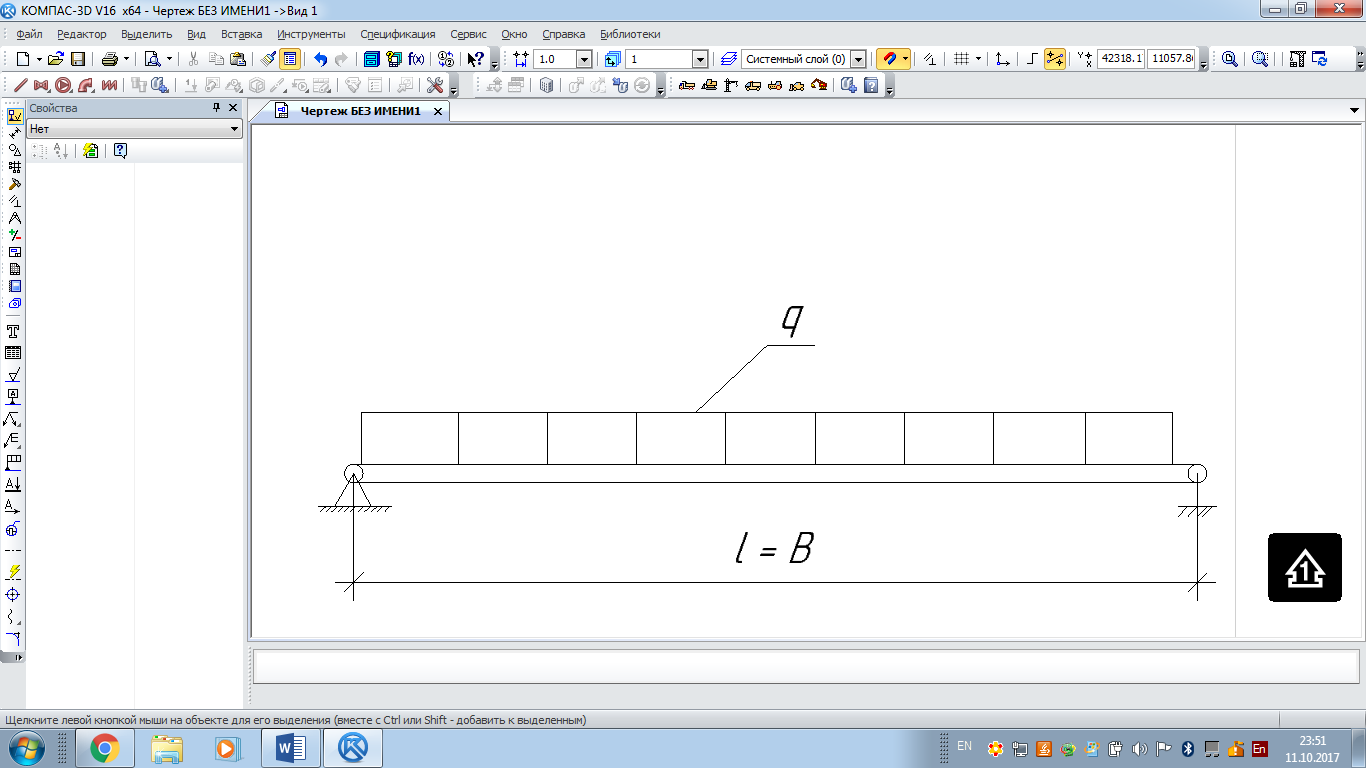 Рисунок 1.2 – Расчетная схема балки настила Подбор сечения балки настила осуществляется следующим образом. Нагрузки на балку настила: - нормативная нагрузка (на 1 м) qн = 1,02 ∙ (tн1 ∙ ρст + pn) ∙ a (1.1.3) где 1,02 – коэффициент, учитывающий собственный вес балки; ρст – плотность стали, ρст = 7825 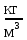 = 78,2 = 78,2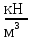 ; ;pn – нормативная нагрузка, 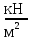 ; ;a – ширина грузовой площади, равная шагу балок настила a = 1,6 м;  30,31 30,31  - расчетная нагрузка 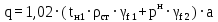 (1.1.4) (1.1.4)где γf1 – коэффициент надежности по материалу для стали, γf1 =1,05; γf2 – коэффициент надежности по временной нагрузке, γf2 =1,2. 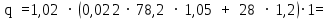 36,11 36,11  Максимальный изгибающий момент Mmax =  (1.1.5) (1.1.5)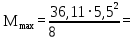 136,54 136,54  . .Требуемый момент сопротивления балки настила из условия прочности на изгиб 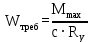 (1.1.6) (1.1.6)Где Ry – расчетное сопротивление по пределу текучести, Ry = 24,5 кН/см2; с – коэффициент пластичности.  506,64 см3. 506,64 см3.По сортаменту подбираем двутавр № 33 с характеристиками: Jx= 9840 см4, Wx =572 см3, вес 1 пог. м балки настила m1 = 42,2 кг. Проверка жесткости (прогиба балки): 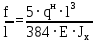 < < 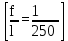 (1.1.7) (1.1.7)где 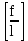 – относительная предельная деформация; – относительная предельная деформация; – модуль упругости, – модуль упругости, 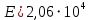 кН/см2. кН/см2.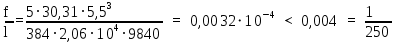 Расход материала по варианту 1: 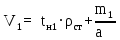 (1.1.8) (1.1.8)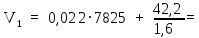 198,525 кг/м2. 198,525 кг/м2.1.2.1 Усложнённая балочная клетка №1 По главным балкам с шагом b = 2 м укладываются вспомогательные балки. По вспомогательным балкам с шагом a'=0,8 м. Необходимые условия: 1) b > a; 2) a'< a.  Условия выполняются. Эскиз усложненной балочной клетки №1 (УБК №1) приведён на рисунке 1.3. Условия выполняются. Эскиз усложненной балочной клетки №1 (УБК №1) приведён на рисунке 1.3. Рисунок 1.3 – Усложненная балочная клетка №1 Толщина настила для усложненной балочной клетки №1  принимаем, используя предыдущие расчеты, из пропорции 8: принимаем, используя предыдущие расчеты, из пропорции 8: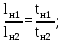 (1.2.1) (1.2.1)Выразим  (1.2.2) (1.2.2)где lн2 – пролет настила для УБК, lн2 = 0,6м. 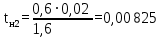 м, м,В соответствии с ГОСТ 19903-74* [2, п. 2.6] принимаем tн2 = 8,5 мм. 1.2.1 Подбор сечения балки настила Определяем нагрузки на балки настила: - нормативная нагрузка рассчитывается по формуле :  , (1.2.3) , (1.2.3) кН/м. кН/м.- расчётная нагрузка рассчитывается по формуле : 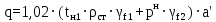 (1.2.4) (1.2.4)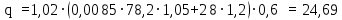 кН/м. кН/м.Максимальный изгибающий момент определяется по формуле 1.1.5: 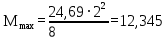 кН/м. кН/м.Требуемый момент сопротивления балки настила из условия прочности на изгиб определяется по формуле 1.1.6: 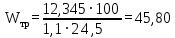 см3. см3.По сортаменту подбираем двутавр № 12 с характеристиками: Jx= 350 см4, Wx = 58,4 см3, вес 1 пог. м балки настила m2 = 11,5 кг. Проверка жёсткости (прогиба балки) по условию 1.1.7: 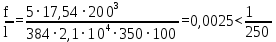 . .Данная балка удовлетворяет требованиям деформативности. 1.2.2 Подбор сечения вспомогательных балок для усложнённой балочной клетки №1 - нормативная нагрузка рассчитывается по формуле:  (1.2.5) (1.2.5)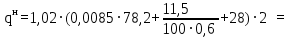 69,26 кН/м; 69,26 кН/м;- расчётная нагрузка рассчитывается по формуле: 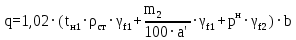 (1.2.6) (1.2.6)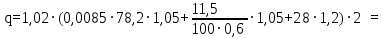 82,80 кН/м. 82,80 кН/м.Максимальный изгибающий момент определяется по формуле 4: 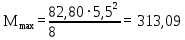 кН/м. кН/м.Требуемый момент сопротивления балки настила из условия прочности на изгиб определяется по формуле 5:  см3. см3.По сортаменту подбираем двутавр № 45 с характеристиками: Jx= 27696 см4, Wx = 1231 см3, вес 1 пог. м балки настила m3 = 66,5 кг. Проверка жёсткости (прогиба балки) по условию 6: 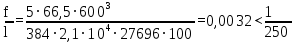 . .Данная балка удовлетворяет требованиям деформативности. Определяем расход материалов по УБК по формуле 13: 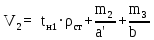 (1.2.7) (1.2.7) кг/м2. кг/м2.1.3.1 Усложнённая балочная клетка №2 По главным балкам с шагом b = 4 м укладываются вспомогательные балки. По вспомогательным балкам с шагом a'=0,6 м Необходимые условия: 1) b > a; 2) a'^< a. Условия выполняются. Эскиз УКБ №2 приведён на рисунке 1.4.  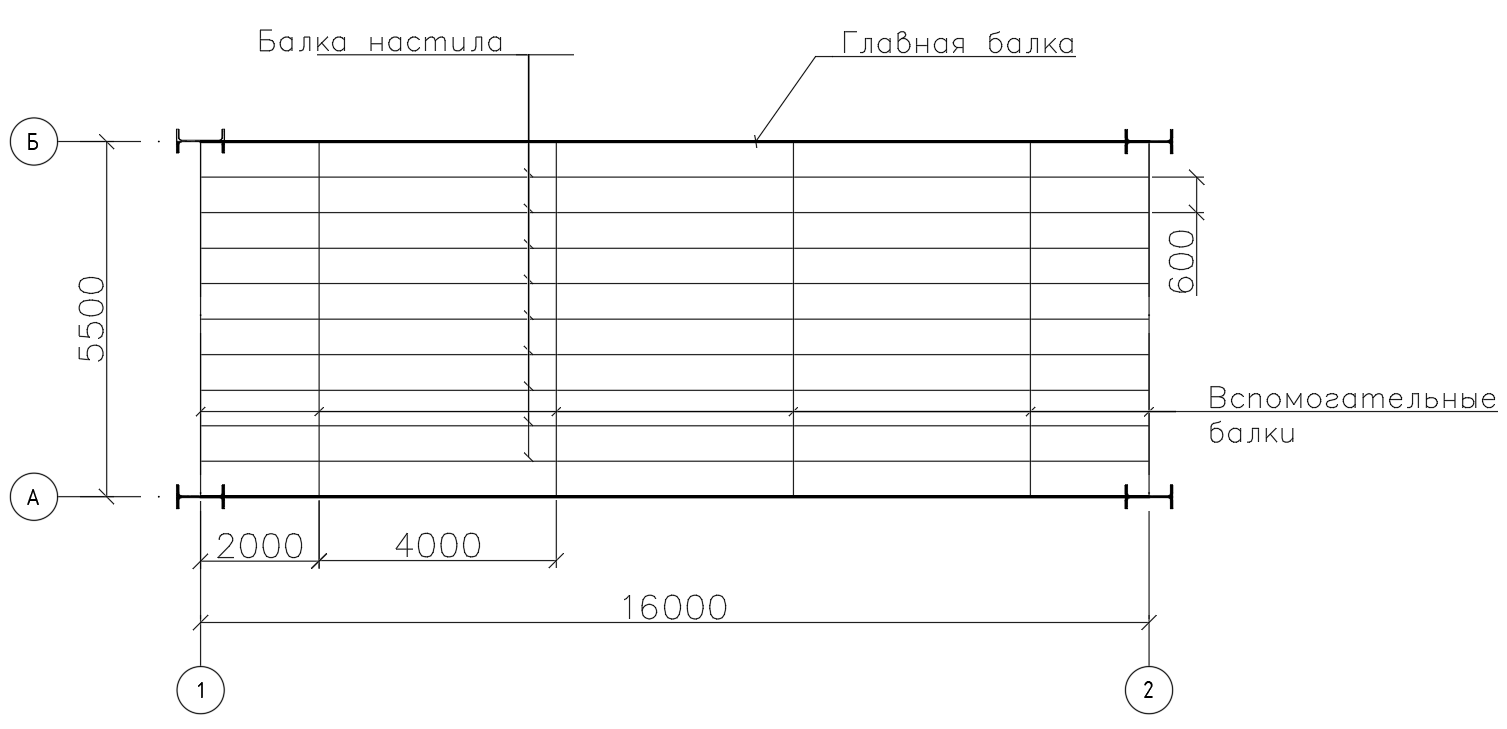 Рисунок 1.4 – Усложненная балочная клетка №2 Толщина настила для усложненной балочной клетки №2  принимаем, используя предыдущие расчеты, из пропорции 1.2.2: принимаем, используя предыдущие расчеты, из пропорции 1.2.2: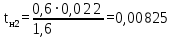 м, м,В соответствии с ГОСТ 19903-74* [2, п. 2.6] принимаем tн2 = 8,5 мм. 1.3.1 Подбор сечения балки настила Определяем нагрузки на балки настила: - нормативная нагрузка рассчитывается по формуле :  , (1.3.1) , (1.3.1) кН/м. кН/м.- расчётная нагрузка рассчитывается по формуле : 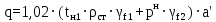 (1.3.2) (1.3.2)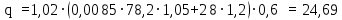 кН/м. кН/м.Максимальный изгибающий момент определяется по формуле 1.1.5:  кН/м. кН/м.Требуемый момент сопротивления балки настила из условия прочности на изгиб определяется по формуле 1.1.6: 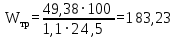 см3. см3.По сортаменту подбираем двутавр № 20 с характеристиками: Jx= 1840 см4, Wx = 184 см3, вес 1 пог. м балки настила m4 = 21,0 кг. Проверка жёсткости (прогиба балки) по условию 6: 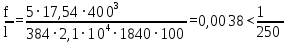 Данная балка удовлетворяет требованиям деформативности. 1.3.2 Подбор сечения вспомогательных балок для усложнённой балочной клетки №2 - нормативная нагрузка рассчитывается по формуле: 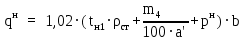 (1.3.3) (1.3.3)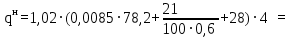 118,38 кН/м; 118,38 кН/м;- расчётная нагрузка рассчитывается по формуле:  (1.3.4) (1.3.4)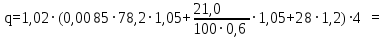 141,43 кН/м. 141,43 кН/м.Максимальный изгибающий момент определяется по формуле : 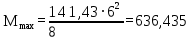 кН/м. кН/м.Требуемый момент сопротивления балки из условия прочности на изгиб определяется по формуле 5:  см3. см3.По сортаменту подбираем двутавр № 60 с характеристиками: Jx= 76806 см4, Wx = 2560 см3, вес 1 пог. м балки настила m4 = 108 кг. Проверка жёсткости (прогиба балки) по условию 6: 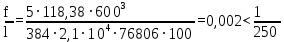 . .Данная балка удовлетворяет требованиям деформативности. Определяем расход материалов по УБК по формуле 14:  (1.3.5) (1.3.5) 128,51 кг/м2. 128,51 кг/м2.К дальнейшей разработке принимаем вариант с меньшим расходом материала, т.е. УБК №2. 2 РАСЧЕТ И КОНСТРУИРОВАНИЕ ГЛАВНОЙ БАЛКИ 2.1 Сбор нагрузок Главная балка проектируется в виде сварного симметричного двутавра. 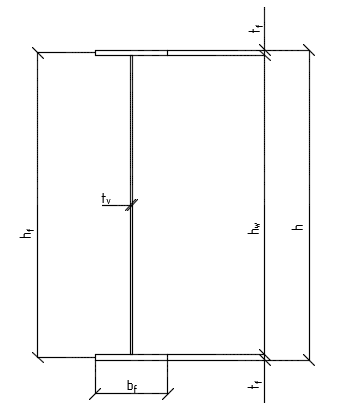 Рисунок 2.1 – Главная балка Определим нагрузки на главную балку. Нормативная нагрузка определяется по формуле:  (2.1.1) (2.1.1)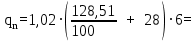 179,22 кН/м 179,22 кН/мРасчетная нагрузка определяется по формуле 15: 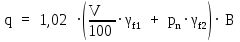 (2.1.2) (2.1.2)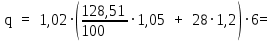 213,89 кН/м 213,89 кН/мОпределим максимальный изгибающий момент по формуле:  кН·м кН·мОпределим максимальную поперечную силу по формуле: 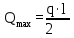 (2.1.3) (2.1.3)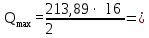 1711,12 кН. 1711,12 кН.Требуемый момент сопротивления балки настила определим по формуле: 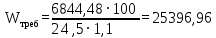 см3. см3.2.2 Выбор высоты главной балки Поскольку момент сопротивления балки выходит за пределы сортамента, то сечение балки проектируем составное, сварное из трех листов. 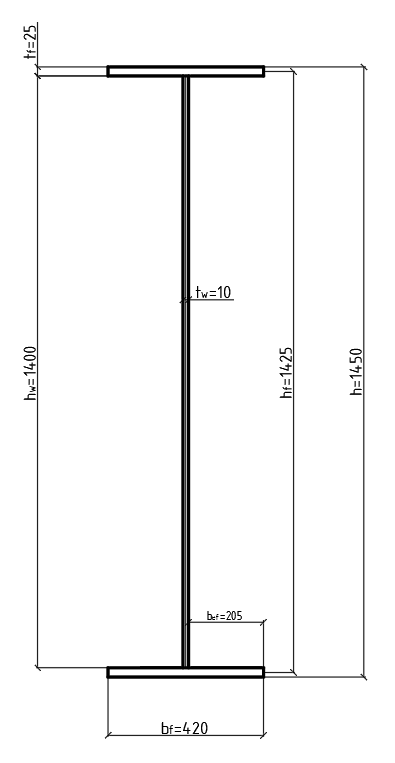 Рисунок 2.2 – Геометрические характеристики сечения главной балки Высота главной балки определяется по двум условиям: h≥hmin; h≈hopt; Первое условие обеспечивает жесткость главной балки, второе условие – наименьшую материалоёмкость балки. Минимальная высота балки определяется по формуле:  (2.2.1) (2.2.1)где l = A – пролет главной балки;  – величина, обратная допустимому относительному прогибу главной балки, – величина, обратная допустимому относительному прогибу главной балки,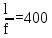 . .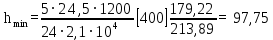 см смОптимальная высота балки из опыта проектирования определяется по формуле: 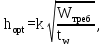 (2.2.2) (2.2.2)где k – коэффициент для сварных балок, k = 1,1 tw – толщина стенки, предварительно принимаем tw = 1см. 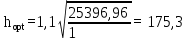 см смПредварительно принимаем высоту балки по максимальной величине h=175,30 см. Задаемся толщиной поясов tf = 25 мм, тогда требуемая высота стенки определяем по формуле 19: 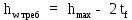 (2.2.3) (2.2.3)hwтреб=175,3 - 2⋅2,5=170,3 см В соответствии с ГОСТ 19903-74* на листовую сталь ([1], п.2.6) принимаем высоту стенки hw=1800 мм. Тогда, окончательная высота балки определяется по формуле : 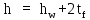 (2.2.4) (2.2.4)h=1800+2⋅25=1850мм 2.3 Компоновка сечения Определяем толщину стенки из условия прочности на срез по формуле :  (2.3.1) (2.3.1)где Qmax – максимальная поперечная сила в балке; Rs – расчетное сопротивление стали срезу, Rs = 0,58∙Ry = 14,79кН/см2; hw– высота стенки балки, см. 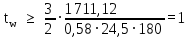 см смПредварительно мы приняли толщину стенки tw=1см, но так как при расчете на срез мы получили tw=1 см, значит толщина стенки была принята правильно. Определим момент инерции стенки балки по формуле:  (2.3.2) (2.3.2) см4 см4Определим требуемый момент инерции для всего сечения балки по формуле: 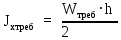 ; (2.3.3) ; (2.3.3) см4 см4Определим требуемый момент инерции поясных листов по формуле 24: 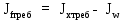 ; (2.3.4) ; (2.3.4) см4 см4Определим требуемую площадь поясных листов по формуле 25: 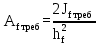 , (2.3.5) , (2.3.5)где hf – расстояние между центрами тяжести поясных листов. 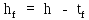 ; (2.3.6) ; (2.3.6)hf=185-2,5=182,5 см Тогда требуемая площадь поясных листов:  111,88 см2 111,88 см2Определим требуемую ширину поясных листов по формуле 26: 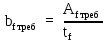 ; (2.3.7) ; (2.3.7)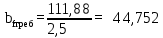 см. см.Окончательно требуемую ширину пояса принимаем в соответствии с ГОСТ 82-70* на листовую сталь ([2], п.2.8) (кратно 5 мм, при этом не меньше 180 мм) принимаем bf = 450мм. Для обеспечения устойчивости пояса должны выполняться условия:  ; ; , ,где bef – свес пояса.  ; (2.3.8) ; (2.3.8) мм мм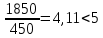 ; ;  Условия выполняются, следовательно, окончательная ширина пояса 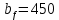 мм. мм.Определим геометрические характеристики принятого сечения по формуле 2.3.9: 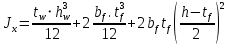 ; (2.3.9) ; (2.3.9)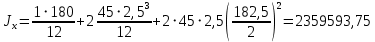 см4 см4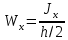 ; (2.3.10) ; (2.3.10)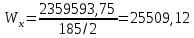 см3 см3Прочность принятого сечения определяем по формуле 2.3.11: 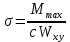 ; (2.3.11) ; (2.3.11)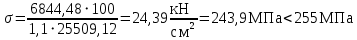 Условие прочности выполняется | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
