Вр. ЖДСУ стрелочная улица (2) (1). Расчет координат стрелочной улицы
 Скачать 330.22 Kb. Скачать 330.22 Kb.
|
|
Ташкентский Государственный транспортный университет Кафедра: «Транспортно-грузовые системы» РГР На тему: « Расчет координат стрелочной улицы» Выполнила:Абдурахмонов А. Ст.гр.ТЛТ-11р Приняла: Эргашева З.В. Ташкент 2023 Содержание: Введение…………………………………………………………………………..3 Назначение стрелочных улиц и их виды и применение……….…………………………………………………………….....4 Координирование центров стрелочных переводов и вершин углов поворота путей………………………………………………………………………………15 Расчет координат стрелочной улицы…………………………………………..16 Список использованной литературы...................................................................19. Введение. Железные дороги нашей страны выполняют большую часть грузовых и пассажирских перевозок, размеры которых непрерывно растут и для успешного освоения их необходимо совершенствовать технические устройства и технологию работы. Станции и узлы являются важнейшими элементами железнодорожного транспорта. На них расположены парки путей, пассажирские и грузовые устройства, локомотивное и вагонное хозяйства, устройства энергоснабжения и водоснабжения, материальные склады, служебно-технические здания и другие сооружения и устройства. Протяжения станционных путей составляет около 60% эксплуатационной длины сети железных дорог. Станции и узлы обеспечивают прием, отправление и пропуск поездов, на станциях выполняются пассажирские и грузовые операции, расформировываются и формируются поезда, ремонтируется подвижной состав, экипируются локомотивы и пассажирские составы, обслуживаются подъездные пути предприятий и другие. Назначение стрелочных улиц и их виды и применение. Стрелочные улицы образуются при последовательной укладке стрелочных переводов на пути для примыкания группы параллельных путей. Стрелочные улицы дают возможность принимать поезда с главного пути на любой путь парка станции, отправлять поезда с любого пути на главный путь, а также переставлять вагоны с одного пути на другой через вытяжной путь. Конструкция стрелочных улиц имеет существенное значение при проектировании крупных станций, она определяет условия работы и влияет в некоторой степени на безопасность движения. От длины стрелочных улиц часто зависят необходимая длина площадки станции и строительные затраты. Классификация стрелочных улиц Стрелочные улицы классифицируются на: простые стрелочные улицы (под углом крестовины, на основном пути); сокращенные стрелочные улицы; под двойным углом крестовины; веерные стрелочные улицы (левосторонние и правосторонние); комбинированные (составные) стрелочные улицы; пучкообразные стрелочные улицы. 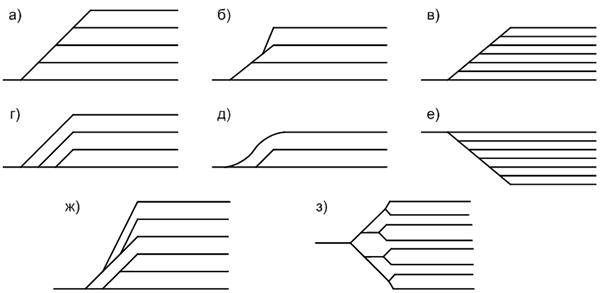 Рис. 1 – Схемы стрелочных улиц: а – под углом крестовины; б – под двойным углом крестовины; в, е – веерные (левосторонняя и правосторонняя); г – на основном пути; д – сокращенная; ж – комбинированная (составная); з – пучкообразная При расчете стрелочных улиц всех видов известными величинами являются расстояния между осями параллельных путей е, радиусы сопрягающих кривых R, данные о стрелочных переводах (тип рельса, марки крестовин, расстояния а, b, Lп). Простые стрелочные улицы Различают два типа простых стрелочных улиц: под углом крестовины (рис. 2, а); расположенную на основном пути (рис. 2, б). 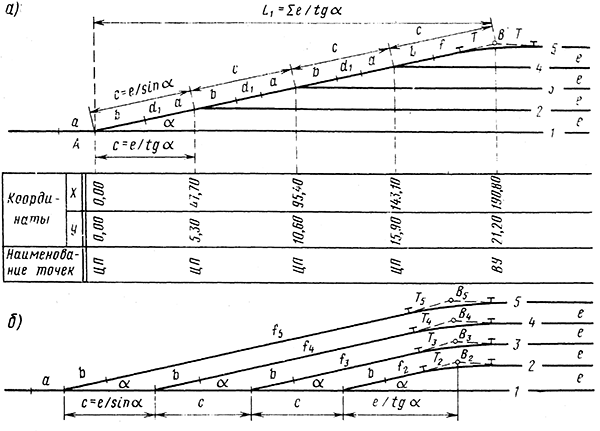 Рис. 2 – Простейшие стрелочные улицы (схемы) При расчете стрелочной улицы под углом крестовины определяют значения С, С1, Т, координаты центров переводов и вершины угла поворота (точки В). Проверяется достаточность вставки f для разгонки уширения колеи. Значения Т, К и f определяются по приведенным формулам предыдущей лекции. Длина соединительной прямой от торца крестовины до стыка рамного рельса следующего перевода d1 = e/sinα – Lп. Длина стрелочной улицы по проекции от центра первого перевода до вершины угла поворота крайнего пути L1 = Σе/tgα = ΣеN. Где N – знаменатель марки крестовины. Центр первого перевода принимают за начало координат и, проецируя на горизонтальную ось X и вертикальную ось Y известные расстояния с учетом угла наклона, находят координаты X и Y центров переводов и вершин углов поворота. Для рассматриваемых точек стрелочной улицы X = Σе/tgα; Y = Σе. Координаты вписывают в горизонтальные графы внизу плана стрелочной улицы или в специальную ведомость координат. Подсчеты ведут с точностью до 0,001 м, результат округляют до 0,01 м. Этот же принцип определения координат центров переводов и вершин углов поворота посредством проекции на две оси применяется и при проектировании всех других видов стрелочных улиц. В стрелочной улице, расположенной на основном пути, кривые путей 2, 3 и т.д. концентричны. Радиус R кривой пути 2 обычно задан. Радиусы кривых в последующих путях возрастают на е, т. е. R3 = R2 + е, R4 = R2 + 2е и т. д. Координаты центров переводов и вершин углов поворота легко определяются при известных значениях е, С и а. Достоинством простых стрелочных улиц является хорошая видимость и удобство обслуживания. Недостаток их – значительное увеличение длины горловины при большом количестве путей (пропорционально числу путей). Поэтому простые стрелочные улицы применяются с переводами марки 1/9 преимущественно в небольших парках (до четырех-пяти путей). Из двух видов простых стрелочных улиц предпочтительней под углом крестовины, который имеет прямые пути в пределах полезной длины, что обеспечивает лучшую видимость при маневрах. Если основной путь 1 стрелочной улицы является в то же время главным, надо применять стрелочную улицу под углом крестовины, чтобы на главном пути укладывать меньше стрелочных переводов. Сокращенные стрелочные улицы Сокращенные стрелочные улицы имеют более крутые наклоны (под углом β > α) посредством укладки дополнительной кривой после первого перевода 1 (рис. 3). Обычно известны: тип перевода, минимальное расстояние от центра перевода до начала кривой b1, расстояние между осями путей е и радиус R сопрягающей кривой. В отдельных случаях первое междупутье может быть уширенным (е1 > е). 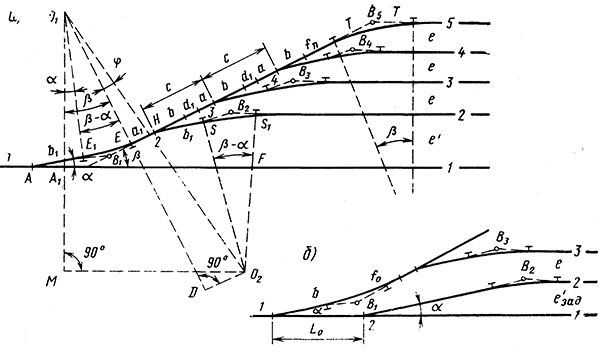 Рис. 3 – Схема сокращенной стрелочной улицы Для определения максимального значения угла наклона β применяются два способа. При первом способе, применяемом обычно, когда первое междупутье е1 больше, чем другие (е), определяется максимальное значение угла β из зависимости sinβ = е/С, где С = Lп + d. Затем находится угол β–α, значение тангенса Т1 для этого угла и значение тангенса Т для угла β: Необходимая расчетная ширина первого междупутья е'р определяется как сумма проекций известных прямолинейных отрезков на вертикальную ось: Приняв что е1 = ер, можно рассчитать координаты центров переводов и вершин углов поворота: 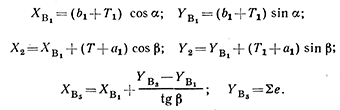 Координаты центров переводов 3, 4 вершин углов поворота на путях 3-4 находятся добавлением к координатам центра перевода 2 проекций на оси X и Y известных отрезков. Особо проверяется величина вставки fп: где Р – расстояние для нормированного уширения колеи в кривой. Если первое междупутье езад задано и больше расчетного е'р, то в первом междупутье укладывается прямая вставка f0: f0 = [(е'зад – е'р] / sinβ. Эта вставка добавляется к а1 при расчете координат Х2 и У2. Если же полученное е'р больше имеющегося междупутья е'зад, необходимо переложить перевод для второго пути на основной путь, как показано на (рис. 3, б) и найти увеличенную f0: f0 = [(е'зад + е) – е'р] / sinβ или рассчитать уменьшенное значение угла β, применив второй способ расчета. Во втором способе расчета определяется значение угла β исходя из заданного размера первого междупутья при вставке f0 = 0. Простейший способ определения угла β основан на построении двух вспомогательных прямоугольных треугольников O1MO2 и O1DO2 общей гипотенузой (рис. 3, а). Из треугольника O1DO2 можно установить вспомогательный угол φ и длину гипотенузы, определив вначале длину катетов O1D и О2D как проекций ломаной линии O1EHSO2: 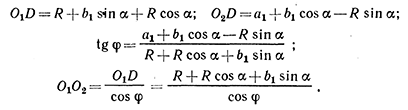 В другом треугольнике O1MO2 вначале надо определить длину катета O1M, выразив его через известные величины b1, R и е, Из построения видно, что Определив угол β при известном угле φ, прежде всего, находят расстояние между центрами стрелочных переводов из условия с = e/sinβ, причем значение с должно быть не менее Lп + d. Дальнейший расчет элементов стрелочной улицы ведется, как и по первому способу. Изложенный метод определения угла β (по второму способу) может применяться для всех сокращенных соединений с обратными кривыми. Достоинством сокращенной стрелочной улицы является то, что она короче по сравнению с простыми стрелочными улицами. Недостаток ее – неудобство маневрирования по путям с обратными кривыми. Применение сокращенной стрелочной улицы целесообразно на путях угольных складов, различных баз, крупных грузовых дворов и на промышленных площадках, где имеются широкие междупутья. Стрелочная улица под двойным углом крестовины Стрелочная улица под двойным углом крестовины (2α), на которой стрелочные переводы 1, 2, 3 (рис. 4) располагаются по схеме попутной укладки. 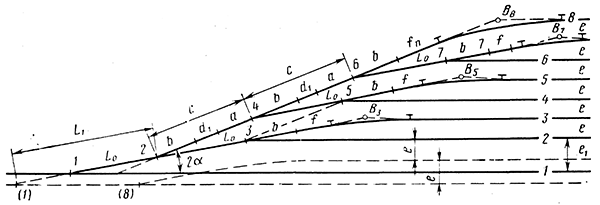 Рис. 4 – Схема стрелочной улицы под двойным углом крестовины В общем случае расстояние между центрами переводов 1-2 и 2-3: L0 = Lп + d. Зная L0, можно определить расчетную ширину первого междупутья и координаты центра перевода 2: Расстояние с между центрами переводов по улице, наклоненной под углом 2α, можно определить, соединив центры переводов 3 и 5 и опустив перпендикуляр из центра перевода 5 на путь 2. Линия 3-5 равна линии 2-4, т. е. равна с. Из построенного вспомогательного треугольника с вершинами в точках 3 и 5 с = 2e/sin2α. Для определения координат центров других переводов и вершин углов поворота используются найденные координаты центра перевода 2, а также известные расстояния с и L0. Координаты вершины угла поворота крайнего пути: Для проверки вставки fп на крайнем пути необходимо вначале определить расстояние от центра перевода 2 до вершины угла поворота на крайнем пути, зная ординату Y2: где Σс – расстояние от центра перевода 2 до центра последнего перевода на прямом участке стрелочной улицы; Тп = Rtgα – тангенс кривой на крайнем пути. В том случае, когда первое междупутье должно быть одинаково с другими, стрелочный перевод 3 для пути 2 укладывается на пути 1 на расстояние e/sinα от стрелочного перевода 1. При нечетном числе путей в парке схема стрелочной улицы изменяется, как показано пунктиром. Расстояние между переводом 1 (при его новом положении) и переводом 2 будет не L0, а несколько больше: Принцип расчета других элементов сохраняется и для измененной схемы. Достоинством стрелочной улицы под двойным углом крестовины является сокращение длины стрелочной зоны, а следовательно, и маневрового рейса. Применяется она преимущественно в горловинах приемо-отправочных парков, имеющих более 4-5 путей. Веерные стрелочные улицы Веерные стрелочные улицы имеют ось в виде ломаной линии; угол направления ее меняется после примыкания каждого следующего пути. Имеются два вида веерных стрелочных улиц: неконцентрические (рис. 5, а); концентрические (рис. 5, б). 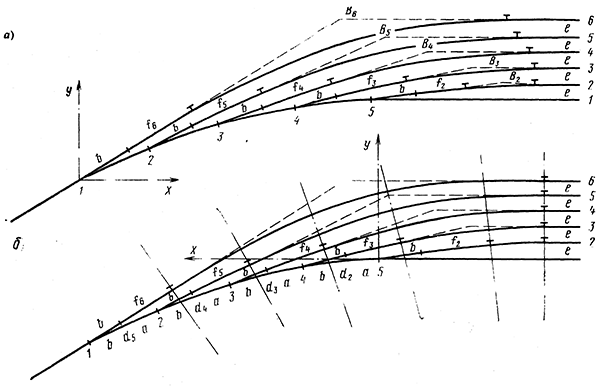 Рис. 5 – Веерные стрелочные улицы (схемы) При расчете неконцентрических стрелочных улиц обычно известно расстояние между осями путей е, радиус R сопрягающей кривой и расстояние между центрами перевода L0, определяемое по схеме попутной укладки. Рассчитывают координаты центров переводов и вершин углов поворота, применяя общий метод проекций на оси X и Y, и определяют элементы кривых для известных углов α, 2α, 3α и т. д. Приняв начало координат в центре перевода 1, получим: 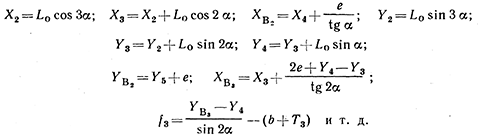 При укладке неконцентрической улицы с постоянным радиусом кривых междупутья в голове парка уширяются, вызывая увеличение объема земляных работ. Для ликвидации этого недостатка можно увеличивать радиусы кривых на каждом последующем пути. При этом надо следить, чтобы междупутья в кривых были не менее допускаемых. В концентрических веерных стрелочных улицах (рис. 5, б) кривые участки концентричны и начинаются в одном створе. Радиус кривой на пути 2 принимают не менее 300 м; для каждого последующего пути радиус кривой возрастает на е. В расчете стрелочной улицы этого вида, кроме координат центров переводов и вершин углов поворота, определяют также длины вставок d и f. Минимальное значение d должно соответствовать требованиям схемы попутной укладки. Недостатком веерной концентрической улицы является изменение вставки d и, как следствие, появление рубок переменной длины при попутной укладке переводов. Веерные улицы применяются в тех случаях, когда из парка надо устроить выход на основной путь, расположенный к парку под углом более 2α, а также для крайних пучков больших парков. Комбинированные (составные) стрелочные улицы Комбинированные (составные) стрелочные улицы возникают при большом числе путей в парках. Чаще всего они представляют собой различные комбинации простых улиц с увеличением угла наклона к основному пути. В качестве примера на (рис. 6) показана улица, которая от стрелочного перевода 2 до стрелочного перевода 4 по своей конструкции является простой улицей под углом крестовины. Участок между переводами 5-7 представляет собой простую улицу на основном пути, но наклоненную к пути 1 под углом α. И наконец, участок, на котором уложены переводы 8-9, представляет улицу под углом крестовины, но наклоненную к пути 1 под углом 3α. Удобно располагать рядом стрелочные улицы 2-4 и 5-7 при ручном обслуживании и устройстве водоотводов от стрелок при электрической централизации. 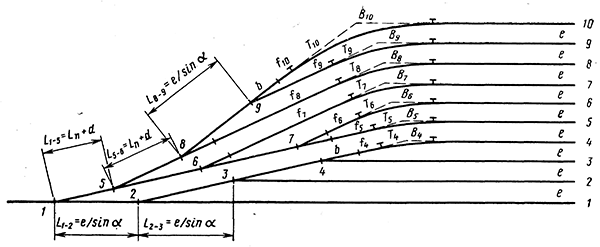 Рис. 6 – Комбинированная (составная) стрелочная улица Расчет координат центров переводов этих улиц весьма прост, так как все углы и расстояния L0 и с известны по предыдущим расчетам. Так же легко определяются координаты вершин углов пов орота. Но в этих стрелочных улицах необходимо проверять возможность вписывания кривых заданных радиусов, для чего надо определить величину вставки между торцом крестовины и началом кривой после наиболее удаленных переводов. В данном случае вставки f на путях 6 и 9 должны быть не меньше k1, а на путях 4, 5 и 10 – не меньше Р. В рассматриваемом примере, зная координаты Х8 и Y8 центра перевода 8, можно определить координаты вершины угла поворота пути 10 и вставку f10: 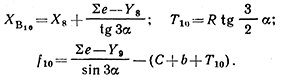 Комбинированные улицы могут также представлять сочетания простых улиц с улицами под углом 2α или веерными. Пучкообразные стрелочные улицы Пучкообразные стрелочные улицы применяются в головах сортировочных парков при наличии горок, укладываются из симметричных стрелочных переводов марки 1/6. При этом головы пучков путей имеют наименьшую длину по сравнению с другими видами улиц. Особенности конструкций пучкообразных улиц рассматриваются в лекциях про сортировочные устройства. 2. Координирование центров стрелочных переводов и вершин углов поворота путей Для уточнения и корректировки масштабной накладки горловины станции, а также определения на местности основных ее элементов, выполняется расчет координат. В качестве осей координат принимается ось одного из главных путей, как правило, главного пути II (ось Х) и ось Y, проходящая через центр первого (по ходу движения) стрелочного перевода, лежащего на оси Х. Таким образом, координаты центра первого стрелочного перевода будут Х (0,00) и Y (0,00). Абсциссы остальных элементов рассчитываются путем сложения или вычитания рассчитанных ранее расстояний между смежными стрелочными переводами к известным уже точкам. Ординаты вычисляются путем суммирования междупутных расстояний. Для того чтобы определиться со знаками «+» и «–», надо представить координатную сетку и разобраться в какой четверти значения X и Yположительные, а в какой отрицательные. Точность расчетов определяется двумя знаками после запятой. Расчет координат приводится в пояснительной записке, а результаты расчета выносят на чертеж. Координатную сетку на чертеже размещают в верхней или нижней частях чертежа. Все координаты выносятся перпендикулярами к соответствующим элементам горловины. Структура и размеры координатной сетки приведены на рис. 1.10.  Рис. 1.10. Структура координатной сетки и ее размеры Расчет координат стрелочной улицы: Р50 1/9 1/11 a=15.42м a=14.43м b= 15.64м b= 19.10м d=6.25м,12.5м X 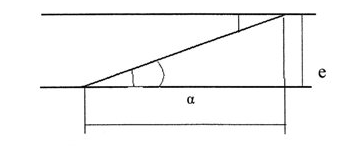 7=460м Y7=0м 7=460м Y7=0м1.X9=X7-  X7-9=460-71,5=388,5 м X7-9=460-71,5=388,5 м X7-9 = X7-9 =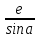 = =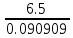 =71,5 м =71,5 мY9=6,5м 2 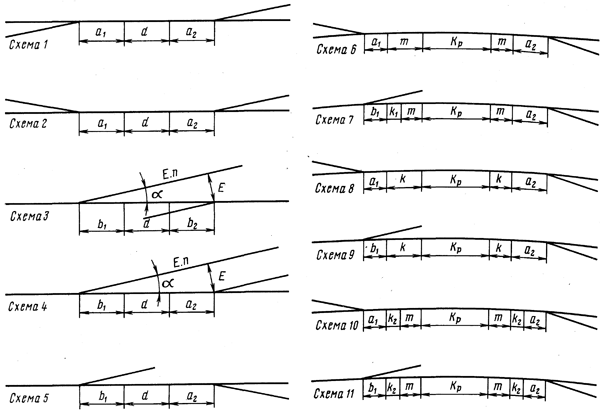 .X11=X9- .X11=X9- X9-11=388,5-43,35=345,1м X9-11=388,5-43,35=345,1м X9-11=a+d+a=14,43+12,5+15,42=43,35м X9-11=a+d+a=14,43+12,5+15,42=43,35мY11=6.5м 3  .X21= X11- .X21= X11- X11-21=345,1-141,2=203,9 м X11-21=345,1-141,2=203,9 м X11-21= X11-21=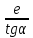 = =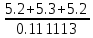 =141,2 м =141,2 мY21=5.3+5.2+5.2=15.7м 4  . XВУ6=X21- . XВУ6=X21- X21-ВУ6=203,9-50,3=153,6 м X21-ВУ6=203,9-50,3=153,6 м X21-ВУ6= X21-ВУ6=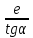 = =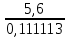 =50.3 м =50.3 м YВУ6=15,7+5,6=21,3м 5 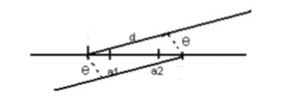 .X15=X 11- .X15=X 11-  X11-15=345,15-47,08=298,07 м X11-15=345,15-47,08=298,07 м X11-15= X11-15=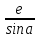 = =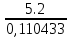 =47,08м =47,08мY15=6,5м 6  .X13=X15+ .X13=X15+ X15-13=298,07+71,5=369,57 м X15-13=298,07+71,5=369,57 м X15-13= X15-13=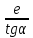 = =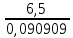 =71,5м =71,5м Y13=0 м 7  . X17=X15- . X17=X15- X15-17=298,07-42,35=255,72 м X15-17=298,07-42,35=255,72 м  X15-17=a+d+a=14,43+12,5+15,42=43,35м X15-17=a+d+a=14,43+12,5+15,42=43,35мY17= 6,5м  8. X19=X17-  X17-19=255,72-46.7=209,02 м X17-19=255,72-46.7=209,02 м X17-19= X17-19=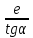 = =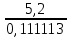 =46,7м =46,7м Y  19= 6,5+5,2=11,7 м 19= 6,5+5,2=11,7 м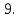 .XВУ4=X19- .XВУ4=X19- X19-ВУ4=209,02-47,7=161,32 м X19-ВУ4=209,02-47,7=161,32 м X19-ВУ4= X19-ВУ4=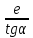 = =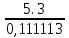 =47.7 м =47.7 мYВУ4=6,5+5,2+5,3=11.7м 1  0. X5=X9+ 0. X5=X9+ X9-5=388,5+44,3=432,8 м X9-5=388,5+44,3=432,8 м X9-5= X9-5=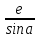 = =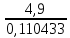 =44,3м =44,3мY5=6,5м 1  1. X3=X5+ 1. X3=X5+ X5-3=432,8+42,35=475,15 м X5-3=432,8+42,35=475,15 м  X5-3=a+d+a=14,43+12,5+15,42=42,35м X5-3=a+d+a=14,43+12,5+15,42=42,35м У3=6,5м У3=6,5м12. X1=X3 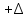 X3-1=475,15+71.5=546,65 м X3-1=475,15+71.5=546,65 м X3-1= X3-1=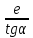 = =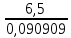 =71.5 м =71.5 м У  1=0 м 1=0 м13.X23 =X5-  X5-23=432,8-46,7=386,1 м X5-23=432,8-46,7=386,1 м X5-23= X5-23=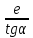 = =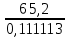 =46,7 м =46,7 м Y23=∑e6,5+5,2=11,7 м 14.X25 =X23-  X23-25=386,1-36,86=349,24 м X23-25=386,1-36,86=349,24 м X23-25 = X23-25 =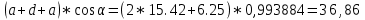 м м 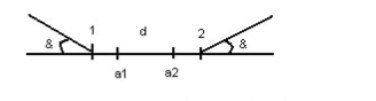 Y23-25=(2*а+d)*sin Y23-25=(2*а+d)*sin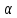 =(2*15.42+6.25)*0.110433=4.09 м =(2*15.42+6.25)*0.110433=4.09 м Y25=11,7+4,09=15,79м Y25=11,7+4,09=15,79м1  5.X27 =X25- 5.X27 =X25- X25-27=349,24-46,8=302,44м X25-27=349,24-46,8=302,44м X25-27= X25-27=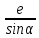 *соs *соs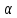 = =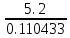 *0.993884=46,8м *0.993884=46,8м Y25-27= Y25-27=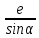 *sin *sin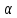 = =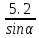 *sin *sin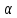 =5,2м =5,2мY27=15,79+5,2=20.99м 1  6.X29 =X27- 6.X29 =X27- X27-29=302,44-47,7=254,74м X27-29=302,44-47,7=254,74м X27-29= X27-29=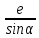 *соs *соs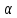 = =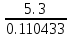 *0.993884=47,7м *0.993884=47,7м Y25-27= Y25-27=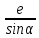 *sin *sin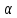 = =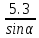 *sin *sin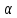 =5,3м =5,3мY27=20,99+5,3=26.2м 17.XВУ-7= X5-  XВУ-7= 432,8-235,8=197 м XВУ-7= 432,8-235,8=197 м XВУ-7= YВУ7*ctg XВУ-7= YВУ7*ctg =26,2*9=235,8 м =26,2*9=235,8 м YВУ7= YВУ7-Y5=32,7-6,5=26,2м YВУ7= YВУ7-Y5=32,7-6,5=26,2мYВУ7=∑e=32,7 м 18.XВУ8= X29-  XВУ-8= 254,74-53=201,7м XВУ-8= 254,74-53=201,7м XВУ8= XВУ8= = = м мYВУ8=∑e=38,3 м 19.XВУ9= X27-  XВУ9=302,44-100=201м XВУ9=302,44-100=201м XВУ9= XВУ9= = = 100 м 100 мYВУ9=∑e=43,6 м 16. XВУ10= X25-  XВУ10=349,24-146,7=202,54 м XВУ10=349,24-146,7=202,54 м XВУ10= XВУ10= = = 146,7 м 146,7 мYВУ-10=48,8 м Список использованной литературы: 1. Железнодорожные станции и узлы. Учебное пособие. Н.В.Правдин, В.Т.Шубко. Издательство «Маршрут». М.: 2005г. 2. Организация переустройства железной дороги под скоростное движение поездов. И.В. Прокудин. Издательство «Маршрут». М.: 2005г. 3. Железнодорожные станции и узлы. Под ред. В.М.Акулиничева, М., Транспорт, 1992. 4. Савченко И.Е., Земблинов С.Е., Страковский И.И. Железнодорожные станции и узлы. М., Транспорт, 1980. |
