автосцепка. КорпусРасчет. Расчет корпуса пружиннофрикционного аппарата
 Скачать 215 Kb. Скачать 215 Kb.
|
|
3. РАСЧЕТ КОРПУСА ПРУЖИННО-ФРИКЦИОННОГО АППАРАТА 3.1.Постановка задачи Исследовать напряженное состояние горловины корпуса поглощающего аппарата в зависимости от продольного усилия и толщины стенок. 3.2.Исходные данные 3.2.1.Схема передачи сил на корпус поглощающего аппарата (см. рис 1.1). 3.2.2.Расчетные схемы горловины корпуса (рис.3.1). 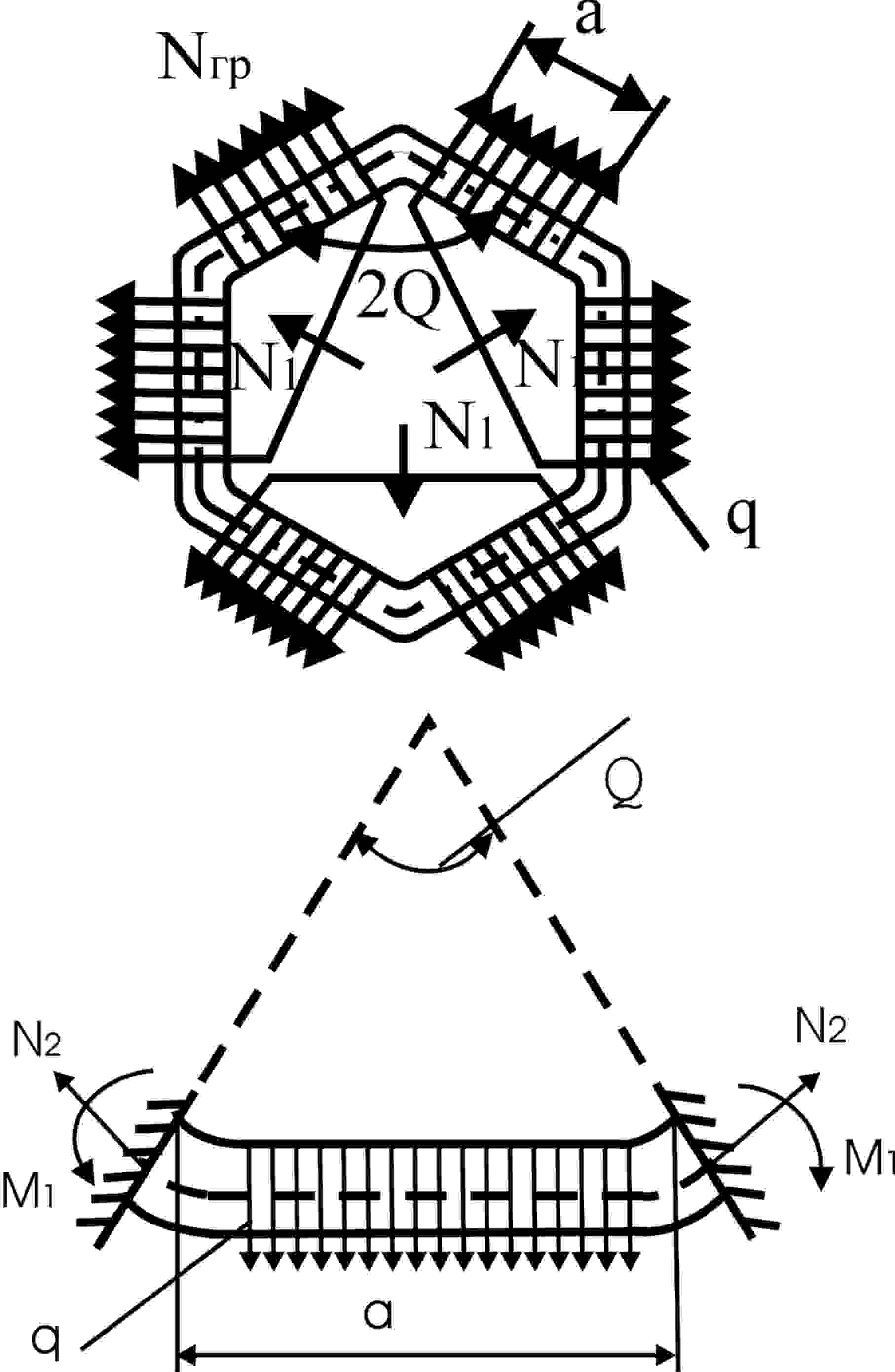 Рис 3.1. Расчетные схемы: горловины корпуса; одной грани шестигранной горловины корпуса. 3.2.3.Основная схема расчетной схемы и эпюры изгибающих моментов от единичных сил и внешней нагрузки (рис.3.2). 3.2.4. Варианты продольных усилий Тс, передающихся на поглощающий аппарат и толщины горловины аппарата (табл.3.1). ТАБЛИЦА 3.1.
3.3. Методика расчета 3.3.1. Определяются усилия, действующие (рис.3.1,а): на желобчатую поверхность горловины, в МН- N1=(Тс(-1))/(3(1cos+sin)); (3.1) на грань, в МН/м q=Nгр/=(N1/(2sinQ))/=N1/( где - коэффициент передачи аппарата при сжатии; 1-коэффициент трения на главных поверхностях корпуса, 1=/sinQ; -средний коэффициент трения, =0,37; Q-половина угла между гранями корпуса аппарата, Q=600; -угол наклона грани клина (см.табл.1.1); Nгр-величина нормальной силы, действующей на одну грань; Тс-усилие сжатия аппарата, МН (см.табл.3.1); -длина грани, =0,1 м. 3.3.2. Составляется расчетная схема. Расчетную схему корпуса аппарата можно представить в виде плоской замкнутой рамы, вырезанной из горловины корпуса двумя параллельными сечениями (см.рис.3.1,а). Вследствии симметрии поперечного сечения корпуса относительно нескольких осей можно рассматривать одну грань шестигранника как балку с защемленными крайними сечениями и с равномерно распределенной нагрузкой q по всей длине грани (см.рис.3.1,б). а  ) Рис. 3.2. Основная система (а) и эпюры изгибающих моментов от единичной силы X1=1 (б) и внешней нагрузки (в). 3.3.3. Устанавливается степень статической неопределимости системы и выбирается основная система (см. рис.3.2,а). Неизвестными усилиями, возникающими в защемлении, будут растягивающая сила N2 и изгибающий момент Х1. Величина силы N2 может быть определена непосредственно из условия равновесия шестигранника: N2=N1/(2cos(Q/2))=N1/ Неизвестной остается только величина изгибающего момента Х1. 3.3.4. Определяются геометрические характеристики сечения грани горловины: площадь F, момент инерции Ix и момент сопротивления Wx относительно нейтральной (горизонтальной) оси х. Расчетное сечение представляет собой трапецию с высотой h и шириной оснований (+hsin) и . Ввиду малости угла можно считать расчетное сечение прямоугольником со сторонами х h. Размер представляет собой толщину стенки корпуса (см.табл.3.1), h-высоту горловины, которая включается в работу при сжатии аппарата. Для аппаратов Ш-1-ТМ и Ш-2-В h=0,19 м. Тогда F=h; Ix=h3/12; Wx=h2/6. 3.3.5. Составляется каноническое уравнение 11х1+1р=0. 3.3.6. Строятся эпюры изгибающих моментов от единичной силы х1=1 (см.рис.3.2,б) и внешних нагрузок q и N2 (см.рис.3.2,в). 3.3.7. Вычисляются коэффициенты и грузовой член канонического уравнения: 11= 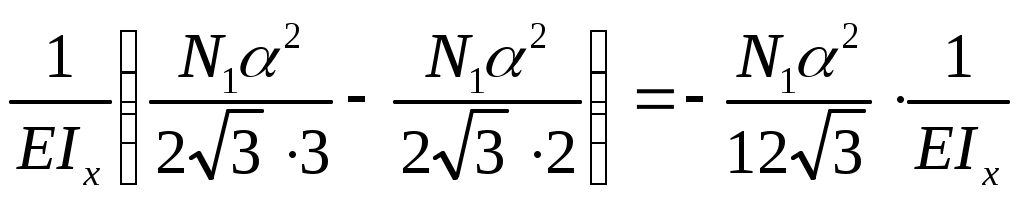 (3.4) (3.4)3.3.8. Решается каноническое уравнение и определяется внутреннее усилие Х1=М=(N1)/(12 3.3.9. Определяется ордината суммарной эпюры изгибающих моментов: для произвольного сечения Мz=М1Х1+Мpz=М+N1z2/(2 в защемлении Мmax=Mz=0=N1/12 3.3.10. Вычисляются напряжения в защемлении =Mmax/Wx+N2/F[], (3.8) где []-допускаемое напряжение; для сталей 30ГСЛ-Б и 32ХО6Л-У []=450 МПа. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
