Главная страница
Навигация по странице:

  • Вариант 13. Цель работы

  • Условие

  • Двоичная цифра

  • 1.1. Коэффициент корреляции

    		•

    ВОФЦС 5(2). Расчет моментных характеристик системы двух случайных величин


    Скачать 34.48 Kb.
    НазваниеРасчет моментных характеристик системы двух случайных величин
    Дата11.09.2022
    Размер34.48 Kb.
    Формат файлаdocx
    Имя файлаВОФЦС 5(2).docx
    ТипЛабораторная работа
    #671005

    ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

    Федеральное государственное бюджетное образовательное учреждение

    высшего образования

    «ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

    (ФГБОУ ВО ИрГУПС)

    Факультет: УТиИТ

    Кафедра: Информационные системы и защита информации

    Дисциплина: Вероятностные основы функционирования цифровых систем

    Лабораторная работа №5

    «Расчет моментных характеристик системы двух случайных величин»

    Выполнил Проверил

    Студент гр. ИС.1-21-1 Ермаков А. А.

    (ф.и.о)

    Липатов П.Д

    (ф.и.о)

    2121059

    (№ студ. билета) (Подпись)

    Иркутск 2022

    Вариант 13.

    Цель работы: Рассчитать дисперсии, ско, ковариации и коэффициент корреляции системы двух случайных величин.

    Условие: Производится тестирование аналого-цифрового преобразователя (АЦП). На вход АЦП подают импульс с амплитудой Uц, соответствующей уровню формирования «1», с определенной частотой. На выходе снимают цифровой сигнал: «1» или «0» и значение амплитуды U*ц, прошедшую через АЦП. Обозначив уровень сигнала U*ц через Х, а значение цифрового сигнала через Y, по представляемой в условии вариантов статистике определить: mx, my, Dx, Dy, cov xy= Kxy, xy. Полученные результаты проанализировать с точки зрения корректности работы АЦП.

    Дано:

    U*ц=6,4 мв
    Х
    6,4
    5,2
    6,4
    5,9
    6,3
    5,0
    6,5
    5,0
    6,3
    4,4

    Двоичная цифра
    Y
    1
    0
    1
    0
    1
    0
    1
    0
    1
    0


    Найдем среднее значение:



    Затем вычислим выборочные дисперсии: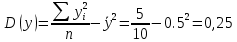





    Среднеквадратическое отклонение: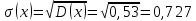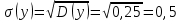



    1.1. Коэффициент корреляции.
    Ковариация.



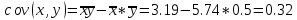    Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:


    Линейный коэффициент корреляции принимает значения от –1 до +1.
    Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
    0.1 < rxy < 0.3: слабая;
    0.3 < rxy < 0.5: умеренная;
    0.5 < rxy < 0.7: заметная;
    0.7 < rxy < 0.9: высокая;
    0.9 < rxy < 1: весьма высокая;
    В нашем примере связь между признаком Y и фактором X высокая и прямая.


    Положительный коэффициент корреляции (прямая корреляция) означает, что изменения двух зависимых величин идут в одном направлении.


    Вывод: Так как в нашем примере ковариация положительна, то с ростом значений амплитуды, снимаемой на выходе после прохождения импульса через АЦП, значения сигнала будет стремиться к единице. Однако только по абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как её масштаб зависит от их дисперсий, для этого нам понадобится значение корреляции которое по расчетам = 0,88, что означает что связь между признаком Y и фактором X высокая и прямая.

    написать администратору сайта