Задача 4. Расчет переходного процесса в цепи второго порядка

• Название: Расчет переходного процесса в цепи второго порядка
• Дата: 28.01.2023
• Размер: 28.1 Kb.
• Имя файла: Задача 4.docx
• Тип: Документы; #909617

Задание 4.

Расчет переходного процесса в цепи второго порядка.

В цепи второго порядка с источником постоянной ЭДС происходит коммутация, в результате которой возникает переходный процесс. Рассчитать ток в катушке iL(t) или напряжение на конденсаторе uC(t) классическим методом.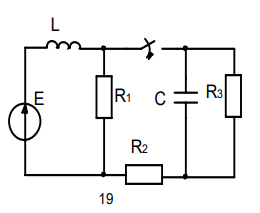





Определим независимые начальные условия (ННУ).

До коммутации ток протекал по цепи E, L, R₁. Его значение:

I_L0 = E/R = 50 / 31 = 1,613 А. Напряжение на R₁ равно Е = 50 В

После замыкания рубильника и установления нового состояния цепи токи в ветвях примут следующие значения.

Сопротивление R₂ + R₃ = 57 Ом. Сопротивление двух параллельных ветвей R = R₁*R₂₃/(R₁ + R₂₃) = 31*57/(31+57) = 20,08 Ом.

Сила тока, текущего через Е I = E/R = 50/20,08 = 2,49 А

Токи, текущие через параллельные ветви

I₁ = E/R₁ = 50/31 = 1,613 А

I₂ = E/R₂₃ = 50/57 = 0,877 А

Напряжение на R₃ = I₂*R₃ = 0,877*40 = 35,08 В. Таким же будет конечное напряжение на конденсаторе

Определим корни характеристического уравнения.
Z = Lp + R₁ + R₂ + (R₃/Cp)/(R₃ +1/Cp) = 0
0,035p + 31 + 17 + (40*0,000028p)/(40 + 1/(0,000028p) = 0

0,035p + 48 + 0,00112p/(40 +35714/p) = 0

0,035p + 48 + 0,00112p /( (40p + 35714)/p) = 0

0,035p² + 48p + 0,00112p/(40p + 35714) = 0

(0,035p² + 48p)(40p + 35714) + 0,00112p = 0
1,4p³ + 3170p² + 1714272p = 0
1,4p² + 3170p + 1714272 = 0
p=0, p= 450,964, p= -2715,25
Корни характеристического уравнения вещественные разные – переходный процесс апериодический, ищем в виде (ток в индуктивности):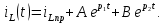


Здесь:

ток принужденный – в конце переходного процесса: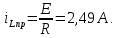


Корни характеристического уравнения 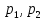уже нашли.

Осталось найти постоянные интегрирования. Для этого используем несколько частных решений: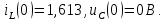



Теперь, учитывая, что из общего решения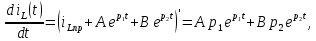



Составим для t=0 и решим систему относительно постоянных интегрирования.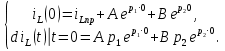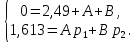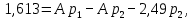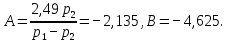







Искомый ток: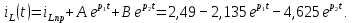