Расчёт ледового перекрытия. Расчёт перекрытия вариант №9 (исправленное). расчет перекрытия
 Скачать 1.57 Mb. Скачать 1.57 Mb.
|
|
Минобрнауки РФ федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный морской технический университет» КАФЕДРА СТРОИТЕЛЬНОЙ МЕХАНИКИ КОРАБЛЯ   Группа: 1484 Учебный год: 2019/2020 Семестр: осенний  Курсовая работа по дисциплине Расчетный практикум на тему: «расчет перекрытия» Дата выдачи г. Срок выполнения г. Номер варианта исходных данных _____ Исполнитель:_____________________________ (Ф.И.О.) Преподаватель:___________________________ (уч.степень, должность,Ф.И.О.)
_________________________________ "____" _______________20__г. (оценка прописью) _________________________ (подпись преподавателя) САНКТ-ПЕТЕРБУРГ 2019 г. Содержание 1. Цель работы…………………………………………………………………………2 2. Исходные данные. Схема перекрытия…………………………………………….2 3. Расчёт ледовой нагрузки. Схема её приложения………………………………….2 4. Создание расчётной модели в Ansys………………………………………………4 5. Подбор оптимального размера конечного элемента……………………………...7 6. Расчётная модель с обозначением граничных условий и приложенной нагрузкой………………………………………………………………………………8 7. Форма деформирования перекрытия в виде полей вертикальных перемещений…………………………………………………………………………..9 8. Поля эквивалентных напряжений для настила и набора……………………….10 9. Поле напряжений в районе точки максимальных эквивалентных напряжений…………………………………………………………………………..12 10. Вывод……………………………………………………………………………..13 11. Код программы…………………………………………………………..……...14 Цель работы. Выполнить расчет перекрытия, нагруженного заданной ледовой нагрузкой, используя программный комплекс ANSYS. Подобрать наиболее предпочтительный размер конечного элемента. Определить деформации и эквивалентные напряжения, возникающие в обшивке и наборе. Из полученных результатов сделать соответствующие выводы. Исходные данные. Схема перекрытия. Геометрические размеры перекрытия приведены в таблице №1.
Таблица №1 - Размеры перекрытия Схема перекрытия представлена на рисунке №1 (страница №3). Расчёт ледовой нагрузки. Схема её приложения. Интенсивность ледовой нагрузки, кПа, определяется в соответствии с Правилами Российского Морского Регистра Судоходства как для бортового перекрытия судна ледового плавания для района ледовых усилений BI: 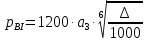 Где: 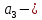 коэффициент, зависящий от категории ледовых усилений; коэффициент, зависящий от категории ледовых усилений;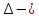 водоизмещение по летнюю грузовую ватерлинию, (т). водоизмещение по летнюю грузовую ватерлинию, (т).Коэффициенты расчета ледовых нагрузок для различных классов судов ледового плавания приведены в таблице №2.
Таблица №2 - Коэффициенты для расчета ледовых нагрузок 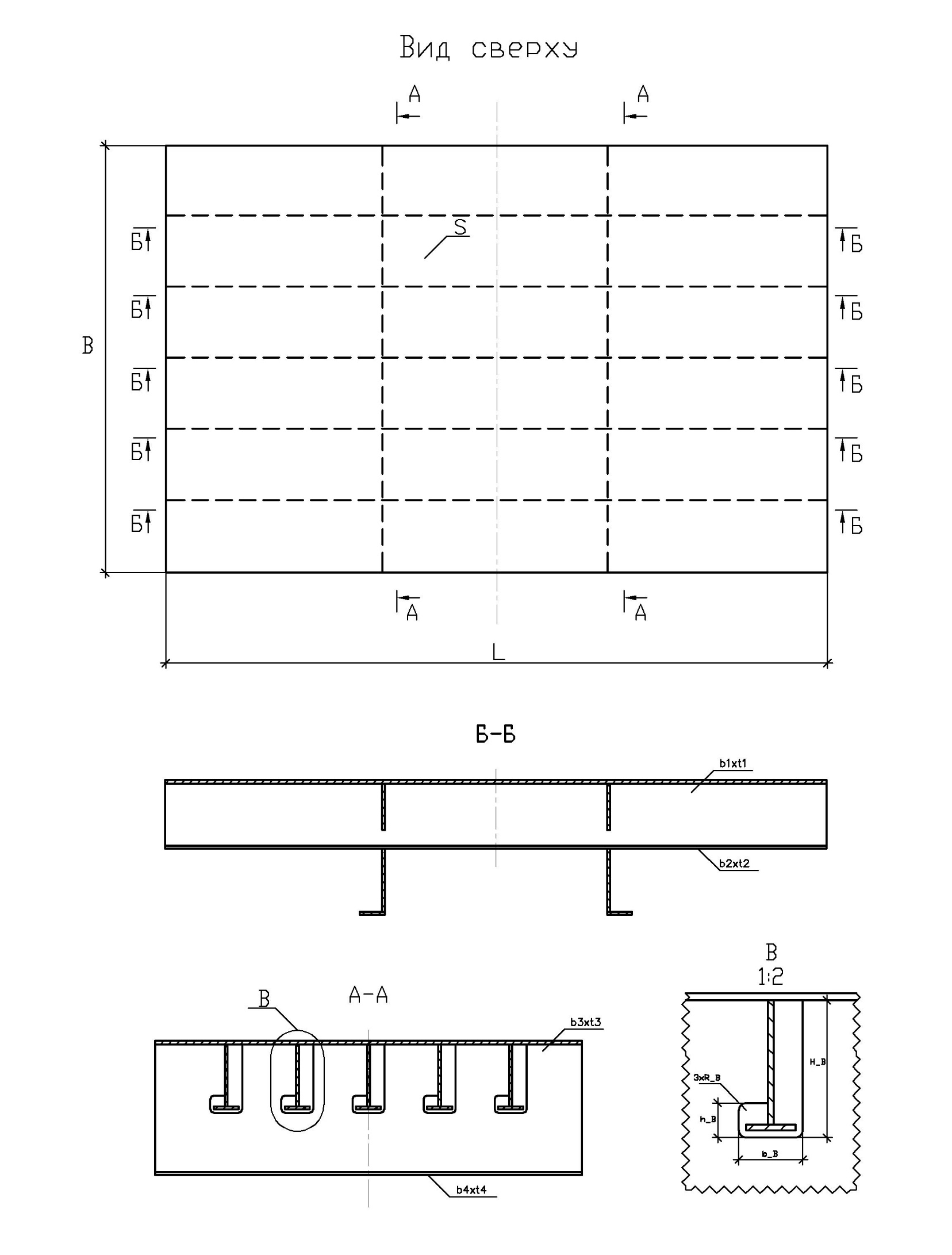 Рисунок №1 – Схема перекрытия. 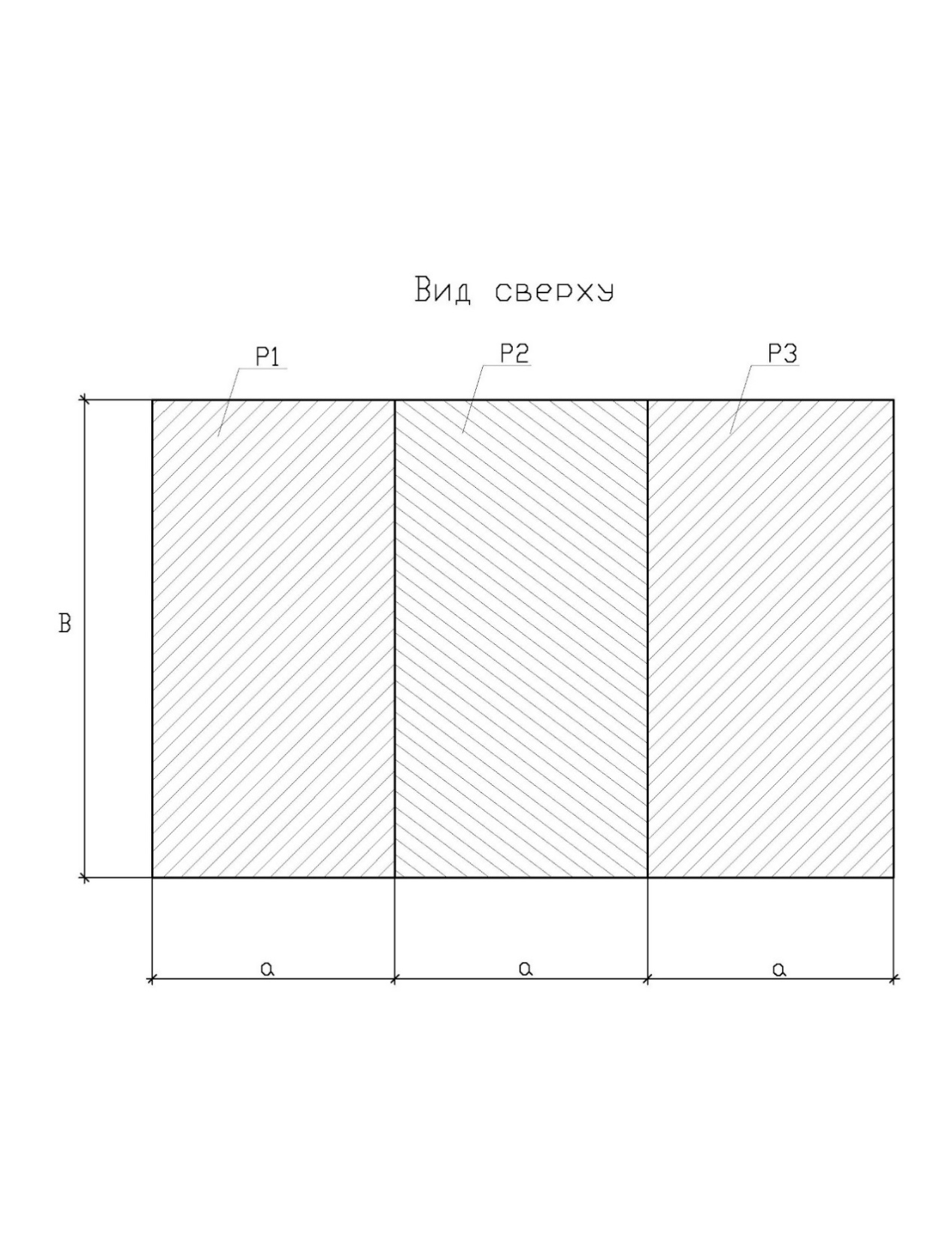 На рисунке №2 приведены три различные области обшивки перекрытия к которым может быть приложено ледовое давление (нагрузка может воздействовать как на одну, так и на несколько областей одновременно). На рисунке №2 приведены три различные области обшивки перекрытия к которым может быть приложено ледовое давление (нагрузка может воздействовать как на одну, так и на несколько областей одновременно).Рисунок №2 – Схема приложения ледовой нагрузки на перекрытие Варианту №9 соответствует класс ледового плавания - Arc 5, и область нагружения – Р2. Интенсивность ледовой нагрузки: 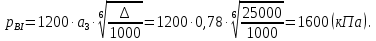 Создание расчётной модели в Ansys. Создание расчётной модели в программном комплексе Ansys подразумевает под собой построение геометрии, задание граничных условий, разбитие геометрической модели на элементы, приложение нагрузки. На рисунках №3,4,5,6 соответственно показаны каждый из перечисленных пунктов. 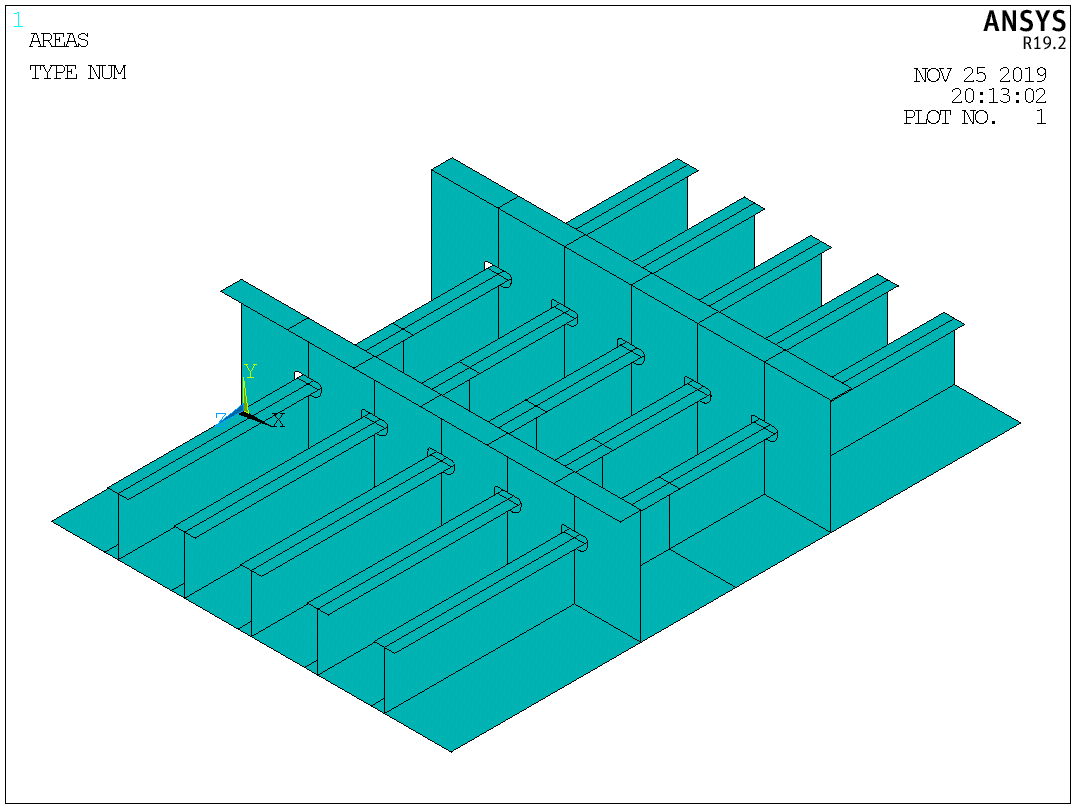 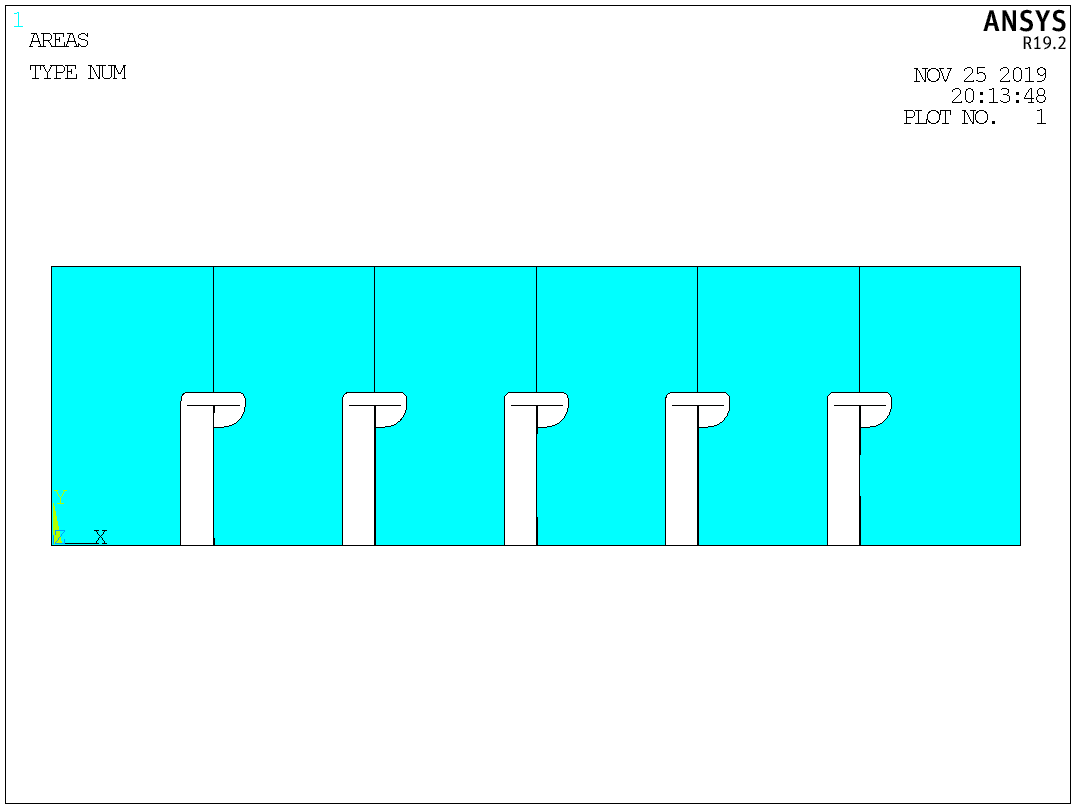 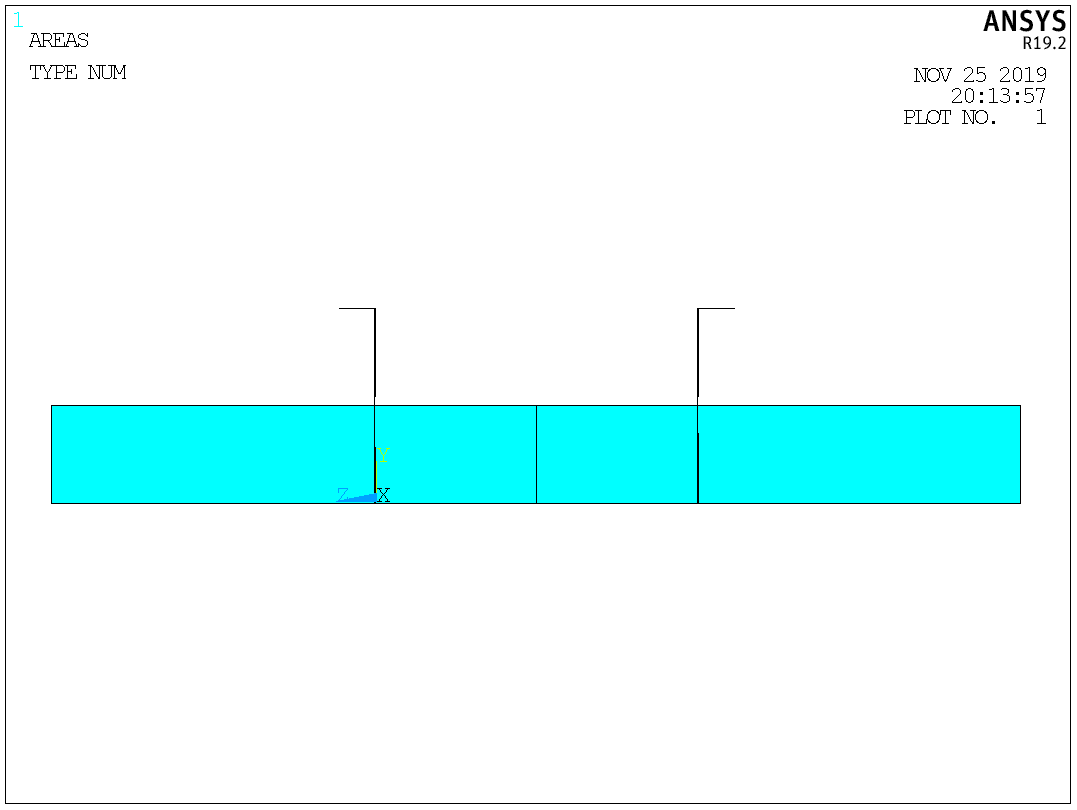 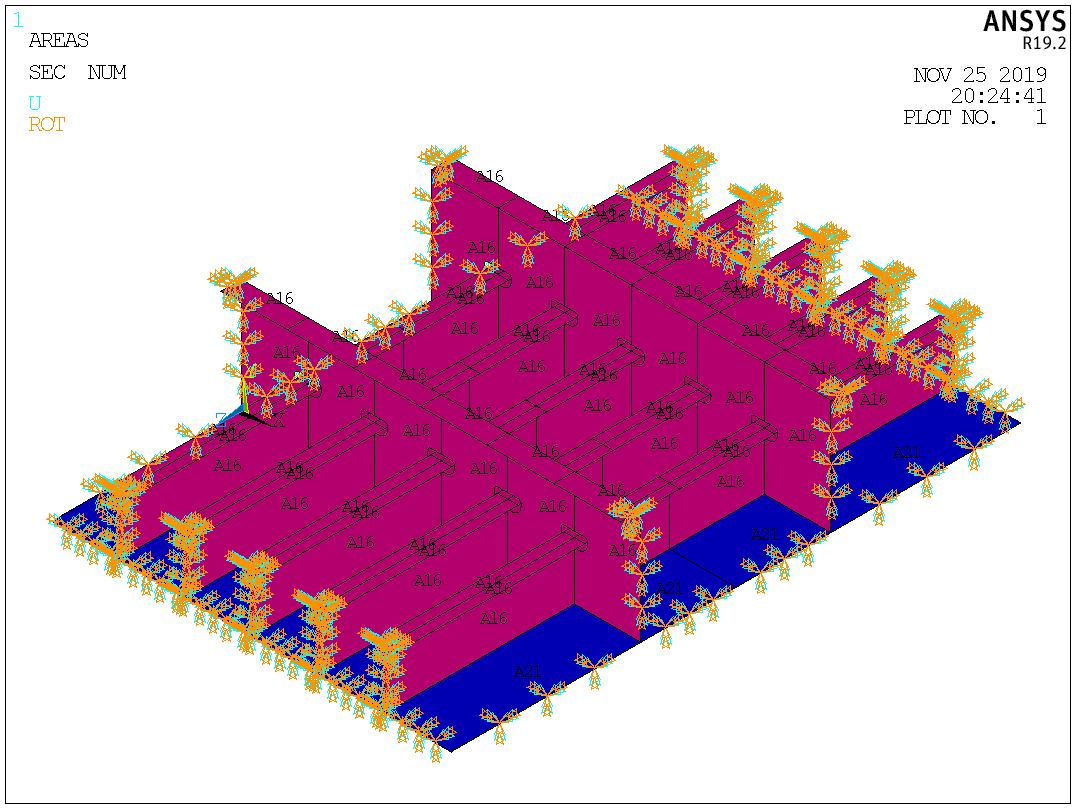 Рисунок №3 – Геометрическая модель Рисунок №3 – Геометрическая модельРисунок №4 – Закрепления (+ отрисовка толщин) 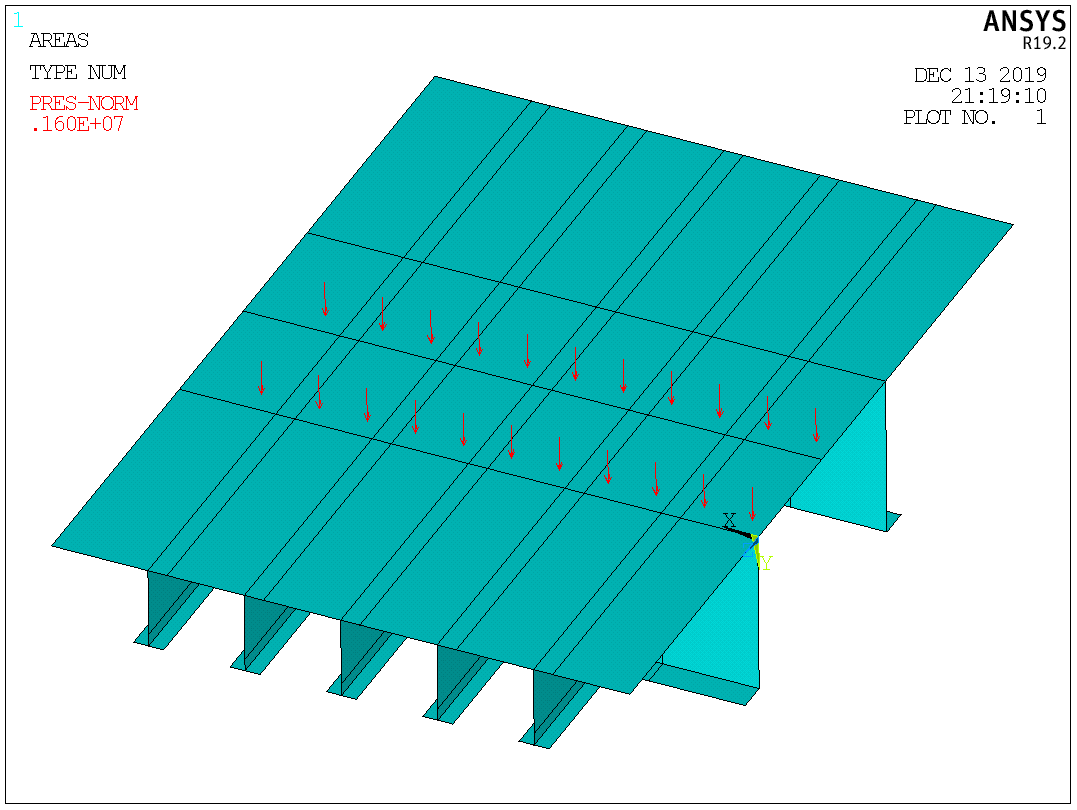 Р Р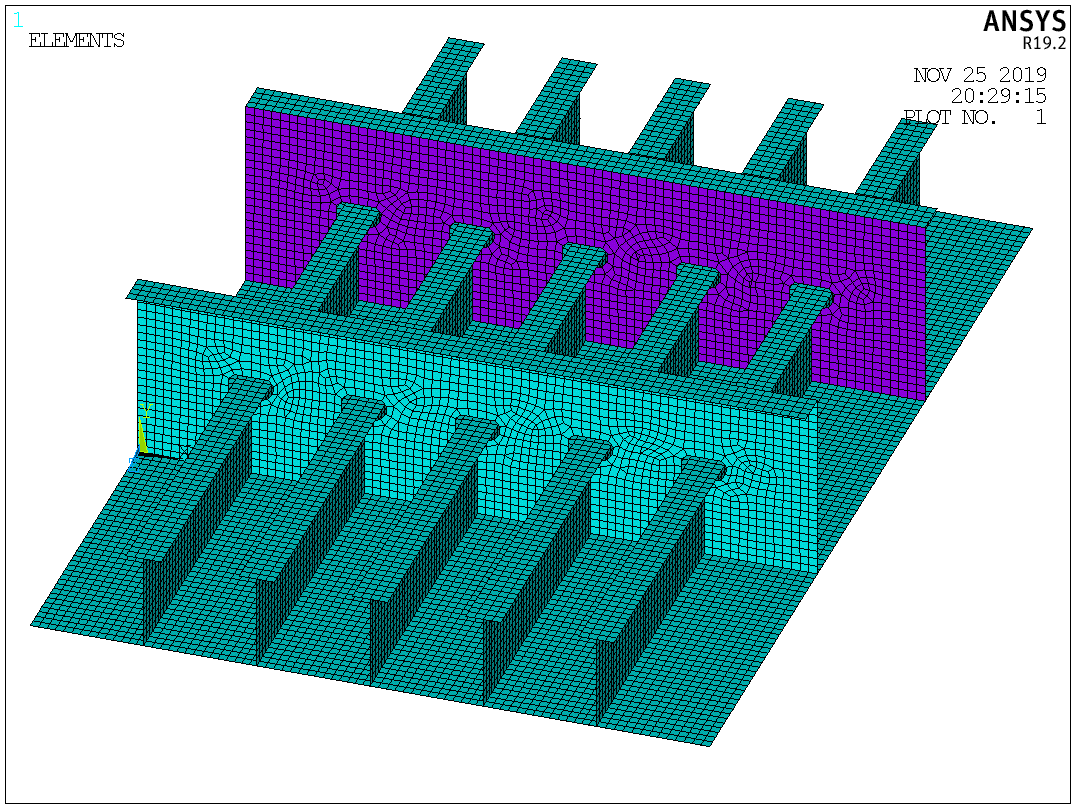 исунок №5 – Конечно-элементная модель исунок №5 – Конечно-элементная модельРисунок №6 – Приложение нагрузки Подбор оптимального размера конечного элемента. Ошибки дискретизации МКЭ уменьшаются с увеличением числа конечных элементов и соответственно с уменьшением их размеров. Однако при постоянном возрастании количества элементов в расчётной модели, значительного повышения точности не происходит, а разность двух решений с относительно близкой степенью дискретизации всё больше стремится к нулю. Помимо этого, время решения задачи стремится к бесконечности. Для получения результатов с приемлемым уровнем ошибок за удовлетворительное время необходимо определить оптимальный размер конечного элемента. В связи с целостностью нашей модели отталкиваться в этом определении будем от ширины полки стрингера 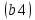 , так как данный размер является наименьшим в перекрытии и относительно большим для быстрого решения. Проведём расчёт суммарных перемещений (USUM) с некоторым шагом изменения размера КЭ и построим кривую зависимости этих значений относительно величины конечного элемента. , так как данный размер является наименьшим в перекрытии и относительно большим для быстрого решения. Проведём расчёт суммарных перемещений (USUM) с некоторым шагом изменения размера КЭ и построим кривую зависимости этих значений относительно величины конечного элемента.Размер конечного элемента будем менять в соответствии со следующей формулой: 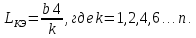 На каждом шаге увеличиваем переменную kна 2 и решаем рассчитываем модель заново. 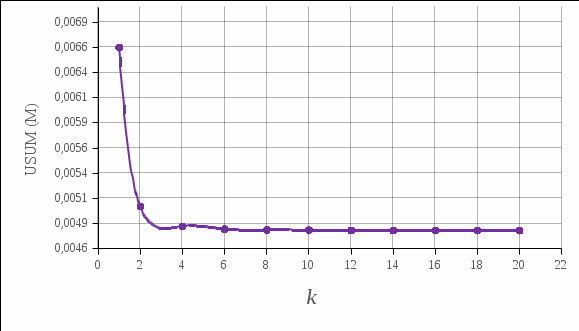 По итогу нескольких расчётов был получен график изменения суммарных перемещений в зависимости от По итогу нескольких расчётов был получен график изменения суммарных перемещений в зависимости от 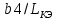 : :График №1 – Зависимость деформацииот k Можно сделать вывод смотря на график №1, что оптимальным размером для конечного элемента в данной расчётной модели является значение 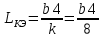 . Записывая это число в миллиметрах получим 17,625 (мм). . Записывая это число в миллиметрах получим 17,625 (мм).Р 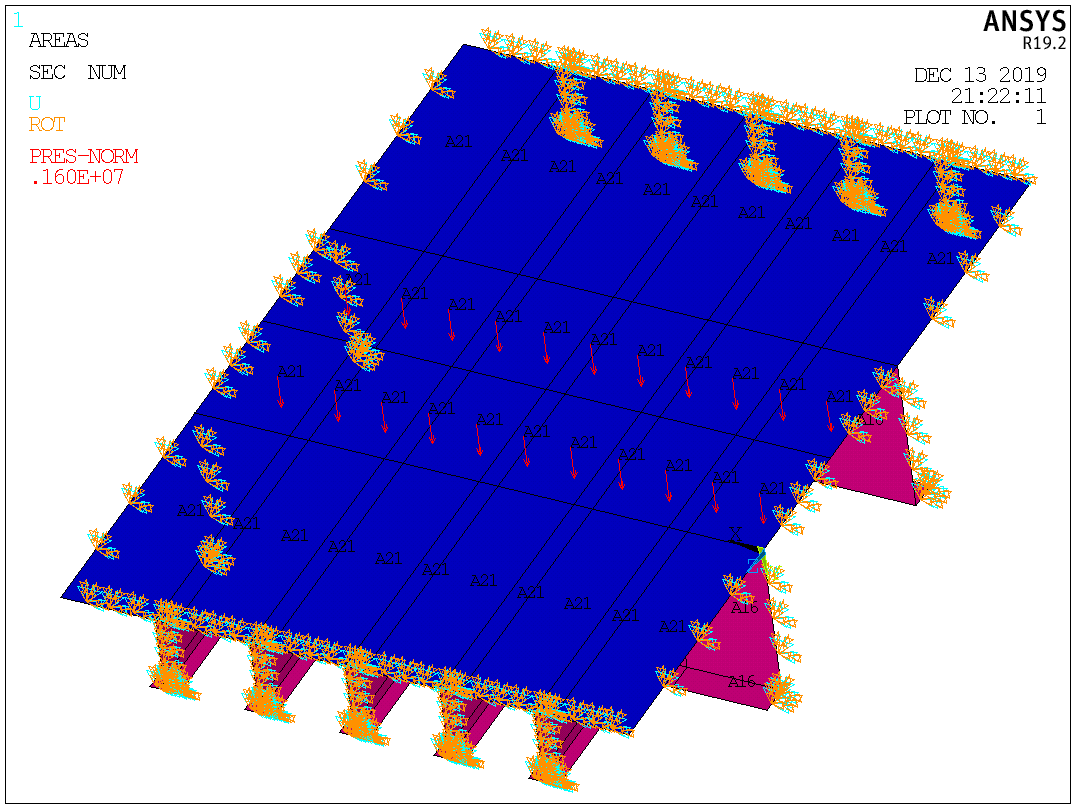 асчётная модель с обозначением граничных условий и приложенной нагрузкой. асчётная модель с обозначением граничных условий и приложенной нагрузкой.Рисунок №7 - Расчётная модель с обозначением граничных условий и приложенной нагрузкой 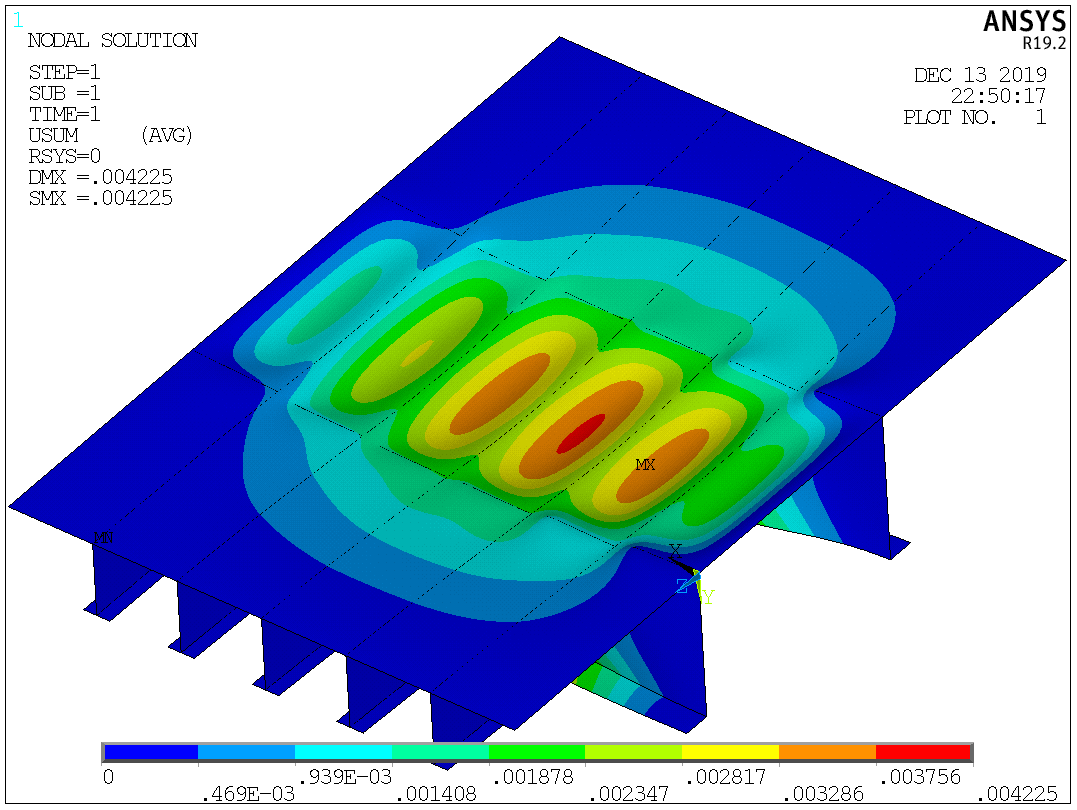 Форма деформирования перекрытия в виде полей вертикальных перемещений. Форма деформирования перекрытия в виде полей вертикальных перемещений.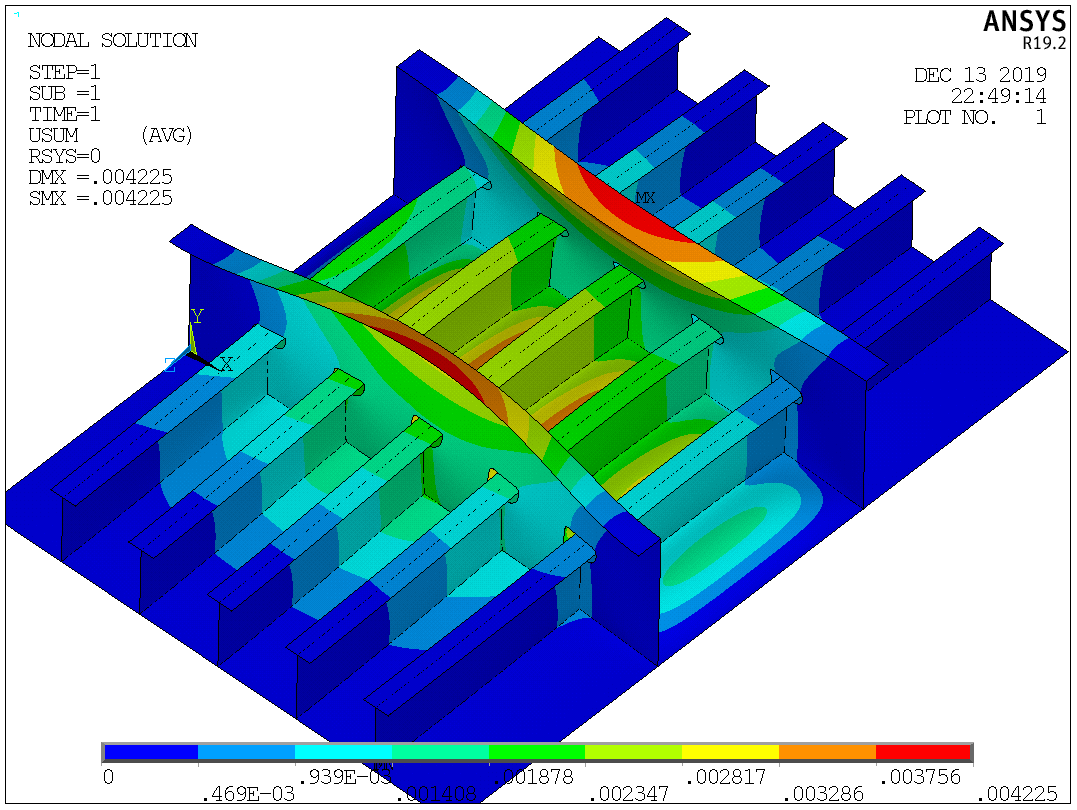 Рисунок №8,9 - Форма деформирования перекрытия в виде полей вертикальных перемещений 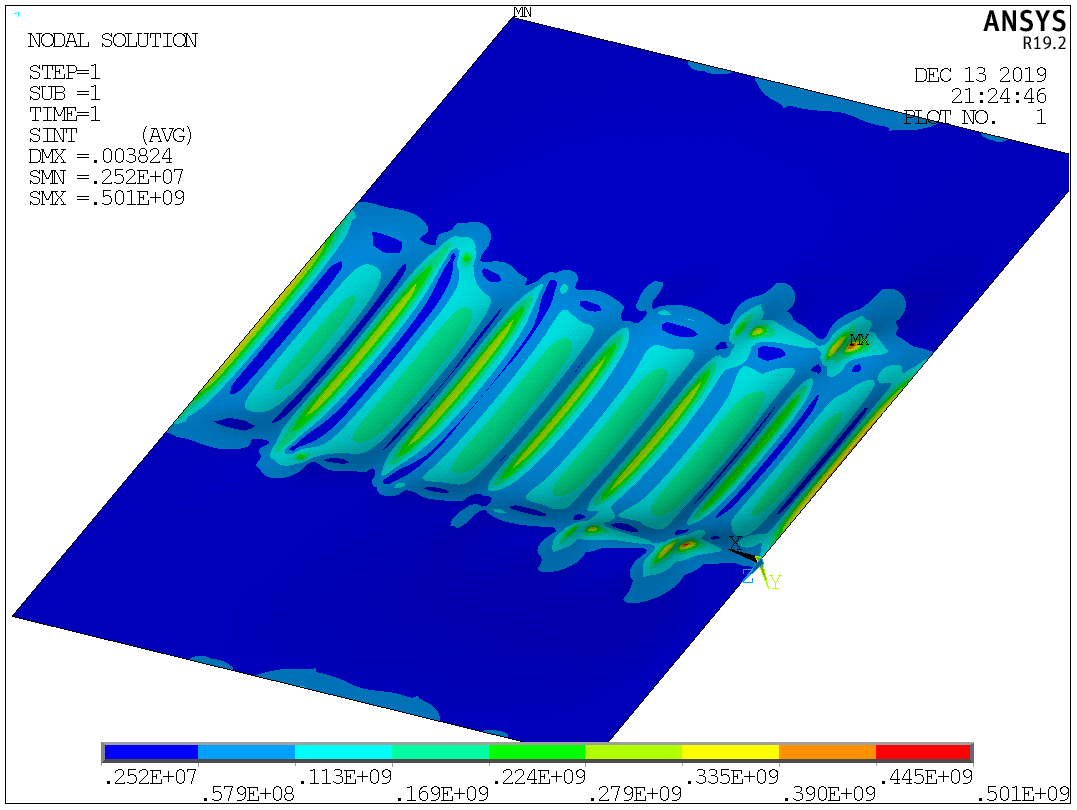 Поля эквивалентных напряжений для настила и набора. Поля эквивалентных напряжений для настила и набора.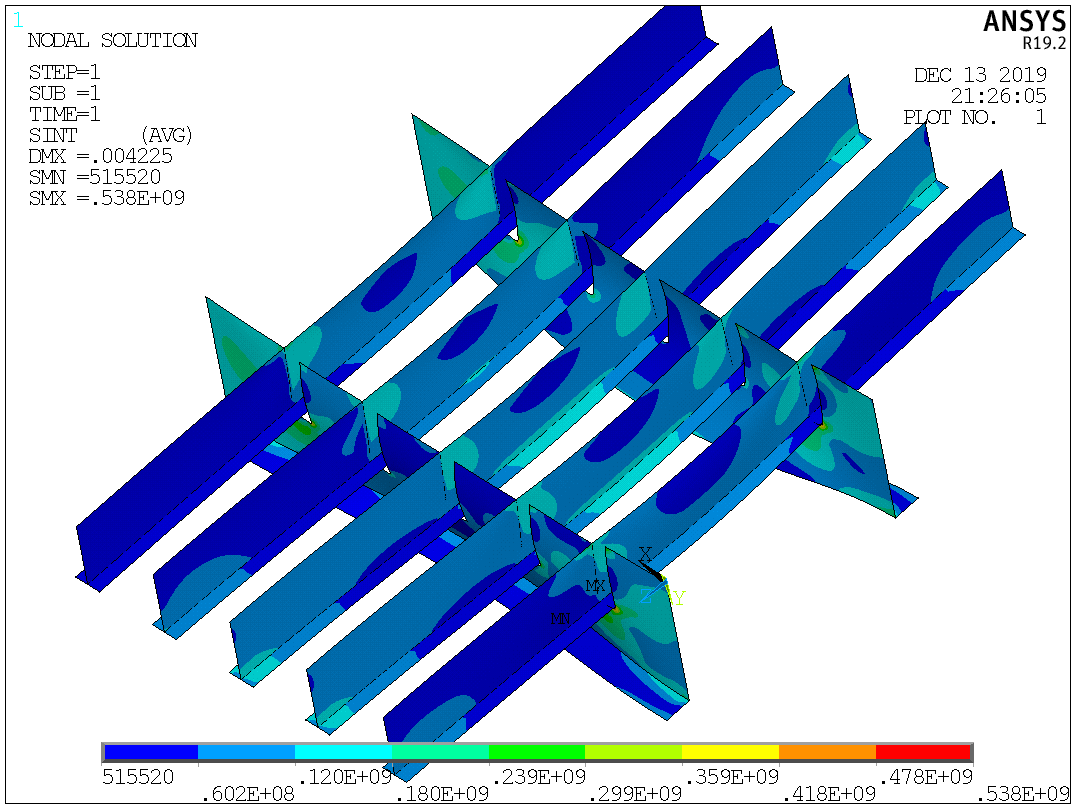 Рисунок №10 - Поля эквивалентных напряжений для настила Рисунок №10 - Поля эквивалентных напряжений для настилаРисунок №11 - Поля эквивалентных напряжений для набора (изометрия) 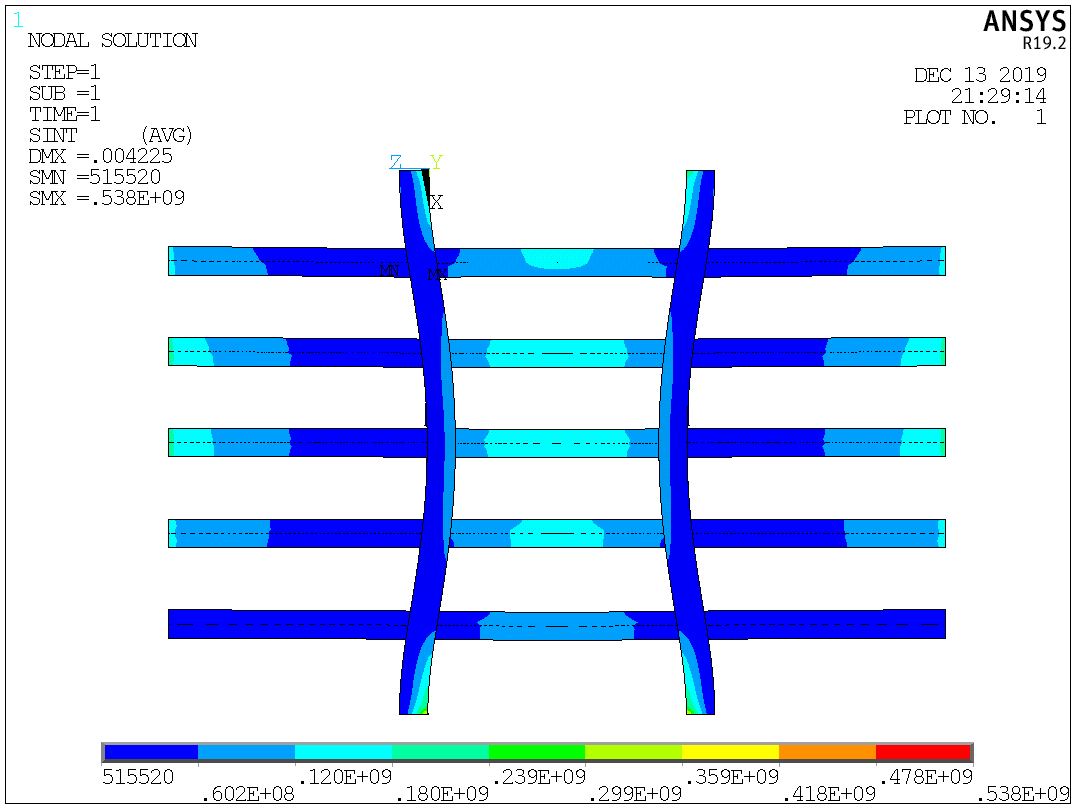 Рисунок №12 - Поля эквивалентных напряжений для набора (вид с верху) Рисунок №12 - Поля эквивалентных напряжений для набора (вид с верху) 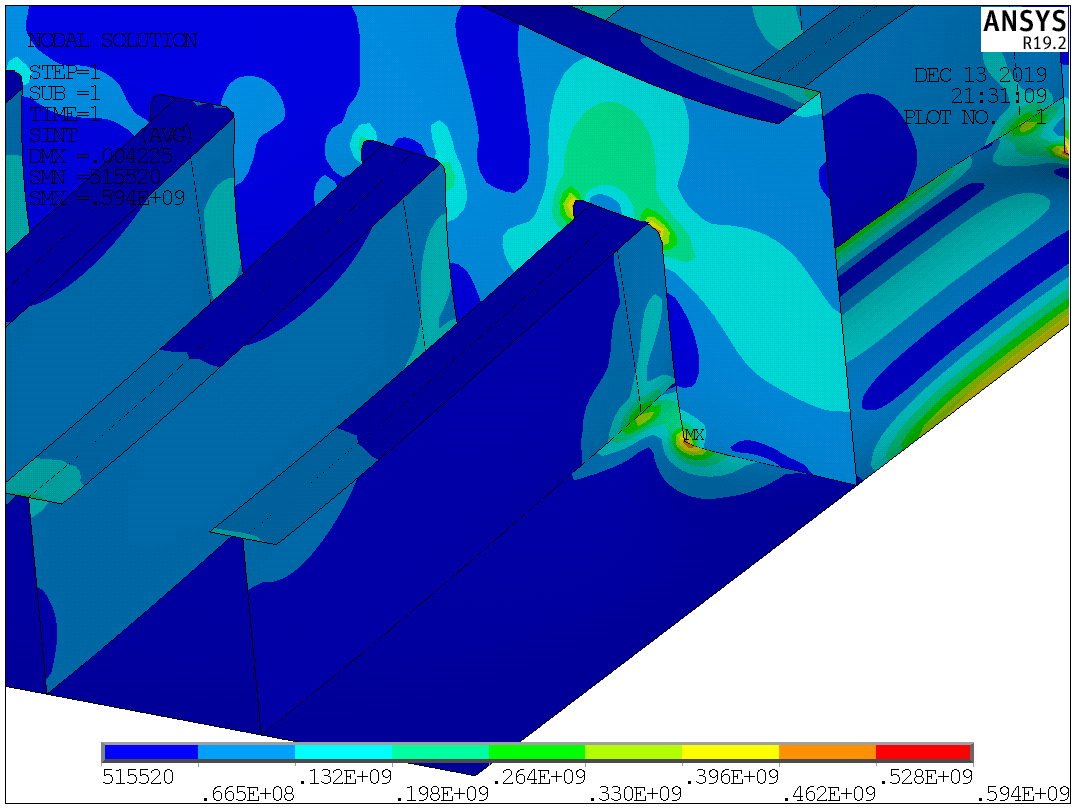 Поле напряжений в районе точки максимальных эквивалентных напряжений. Поле напряжений в районе точки максимальных эквивалентных напряжений.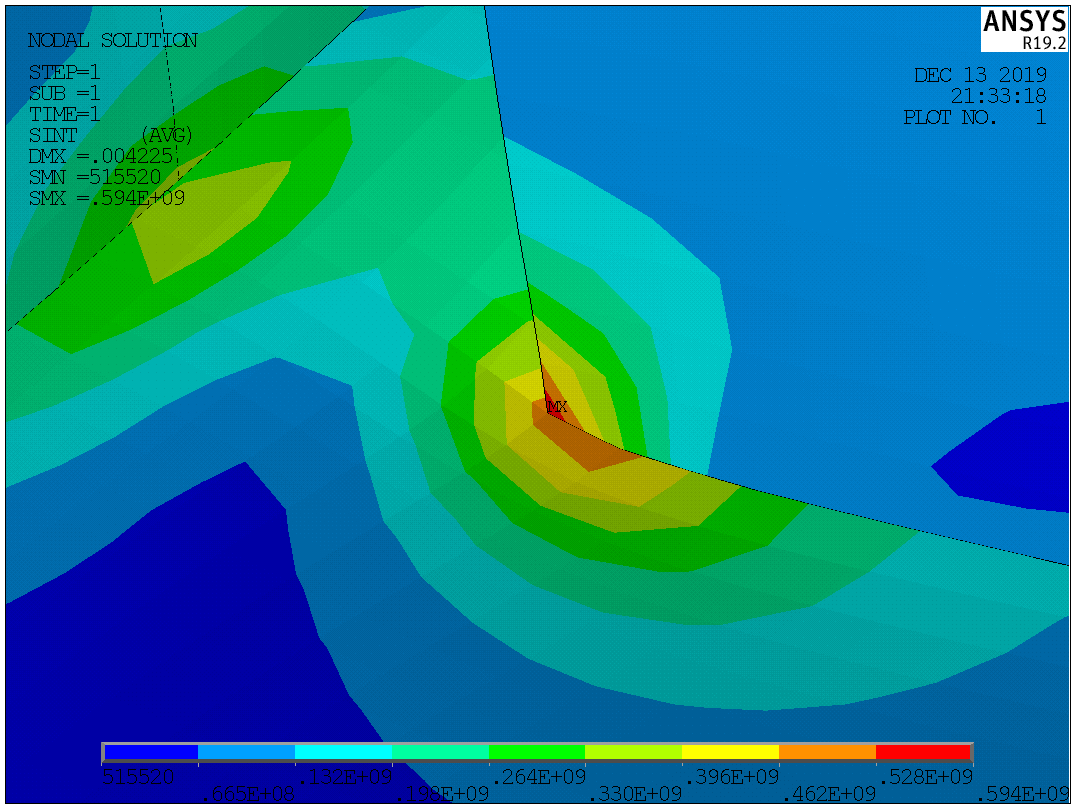 Рисунок №13,14 - Поле напряжений в районе точки максимальных эквивалентных напряжений Выводы. Максимальные эквивалентные напряжения (SINT) составляют 594 (МПа). Такие напряжения наблюдаются в узлах двух крайних вырезов стрингеров для прохода тавра. Наличие максимума в этих точках объясняется тем, что вырез является концентратором напряжений. Также стоит отметить, что действие крупных напряжений принимают на себя центральные пластины к которым, была приложена распределённая нагрузка, в них максимальные напряжения сосредоточены у линий пересечения с таврами и закрепления (для концевых пластин). Наименьшие по размеру напряжения действуют в тавровых поясках и настиле в районе закрепления тавров. Максимальные суммарные перемещения (USUM) составляют 4,23 (мм). Наибольшие деформации возникли в полках стрингеров, несмотря на то, что нагрузка непосредственно к ним не прилагается. Данные деформации вызваны сильным сжатием этих элементов, в следствии чего происходит потеря устойчивого состояния. Такое же явление наблюдается на верхней половине самих стрингеров. Так как нагрузка действует лишь в средней части перекрытия, то и деформации настила в центре оказываются максимальными. Предел текучести основных судостроительных сталей колеблется в значениях от 265 до 440 (МПа) в соответствии с ГОСТ 19282-73, поэтому напряжение в 594 (МПа) для судового перекрытия является достаточно большим. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

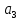
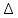 (т)
(т)