реыф. Расчет поперечной рамы в соответствии с методикой сниП
 Скачать 436.98 Kb. Скачать 436.98 Kb.
|
|
Крановые нагрузки При движении колеса мостового крана на крановый рельс передаются силы трех направлений: вертикальная, горизонтальная и продольная. Вертикальная сила Fк (вес груза + вес крана + вес тележки) динамическая, так как вследствие ударов колеса о рельс и рывков при подъеме груза возникают вертикальные инерционные силы, складывающиеся со статической составляющей. При движении крана происходит перераспределение вертикальных сил между колесами (которых у крана не менее четырех), движущимися по рельсу с одной стороны крана. Динамические воздействия колес крана и перераспределение усилий учитываются при расчете подкрановых балок, а при расчете рам вертикальная сила Горизонтальная сила Тк возникает из-за перекосов крана, торможения тележки и т.п. и может быть направлена внутрь пролета или из пролета. Продольная сила возникает от трения колес о рельс и от сил торможения крана и принимается равной 0,1 нормативной вертикальной нагрузки на тормозные колеса крана (половина колес с каждой стороны крана – тормозные). Вертикальная нагрузка на подкрановые балки и колонны определяется от двух кранов при самой невыгодной их расположении. Расчетное усилие, передаваемое на колонну колесами крана, можно определить по линии влияния опорных реакций подкрановых балок по формуле где φс – коэффициент сочетания нагрузок [2], [3, таблица 5]; в нашем случае φс=0,95; у – ордината линии влияния (рисунок 2.2). 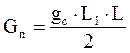 , (2.4) , (2.4)Подставляя значения, получим 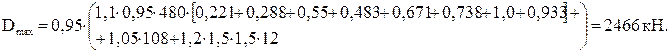 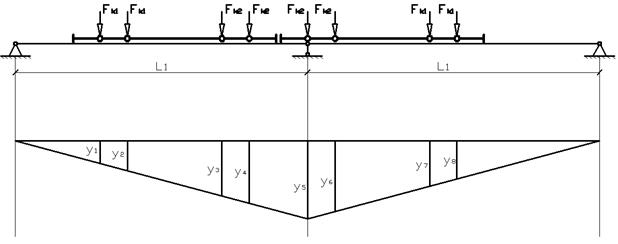 Рисунок 2.2 – Определение ординат линий влияния На другой ряд колонны также будут передаваться усилия, но значительно меньшие (см. рисунок 2.3). 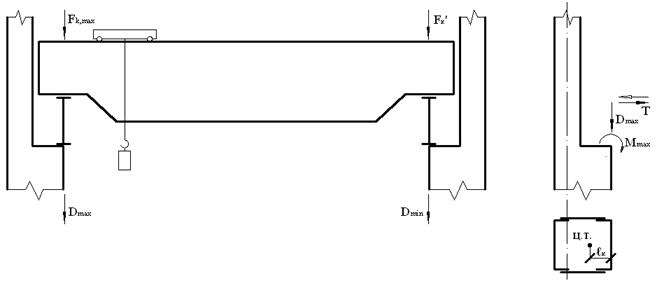 Рисунок 2.3 – Передача усилий от мостового крана на колонны Силу 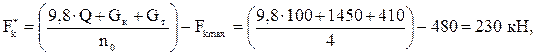 где Тогда 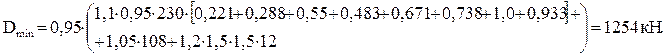 Силы Силы 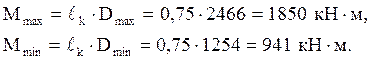 Горизонтальная сила где 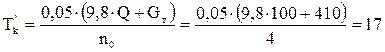 кН. кН.Ветровая нагрузка Расчетная линейная ветровая нагрузка, передаваемая на стойку рамы в любой точке по высоте при отсутствии продольного фахверка, определяется по формуле где с – аэродинамический коэффициент, зависящий от расположения и конфигурации поверхности; для вертикальных стен Линейная распределенная нагрузка при высоте: - до 10 м – - 20 м – - 30 м – Методом интерполяции находим линейная распределенная нагрузку при высоте - 16,57 м – - 23,87 м – Ветровая нагрузка, действующая на участке от низа ригеля до наиболее высокой точки здания, заменяется сосредоточенной силой, приложенной в уровне низа ригеля рамы. Величина этой силы от активного давления и отсоса определяется по следующим формулам Эквивалентные линейные нагрузки активного давления и отсоса: Моменты от нагрузок на стойках Mp (рисунке 3.1, в); коэффициенты берем по таблице 3.2: kA=0,286; kB= –1,202; kC= –0,658. Тогда MA=kA×M=0,268×(–107)= –29 кН×м; MB=(1+kB)×М= (1–1,202)×(–107)=22 кН×м; MB=E×Ip/(1/2)=2×E×4IH×H/(L×H)=8×i×H/L=8×16×i/30=4,27×i; Таблица 3.2 – Коэффициенты для определения реакций и изгибающих моментов в ступенчатой стойке с защемленными концами
Моменты на опорах ригеля (защемленная балка постоянного по длине сечения) Определяем коэффициент канонического уравнения: Угол поворота j= –r1P/r11= 1372/(5,285×i)=260/i. Моменты от фактического угла поворота (M1×j): MA=0,939× i×260/i=244 кН×м; МВ= –1,015×i×260/i= –264 кН×м; MBРИГ=4,27×i×260/i=1110 кН×м; MC= –0,292×i×260/i= –76 кН×м. Эпюра моментов от постоянной нагрузки (М1j+МР) (рисунок 3.1): МА=244–29=215 кН×м; МВ= –264+22= –242 кН×м; MBРИГ=1110–1350= –240 кН×м; MCВ= –37–76= –113 кН×м; MCН=70–76= –6 кН×м. Поперечные силы: на ригеле QB=FR=270 кН; на стойке QАС=(МСН–МА)/Нн= (6–215)/10,5= –20 кН; QАС= (МВ–МСВ)/Нв= (242–113)/6,07= –20 кН. Эпюра представлена на рисунке 3.1, д. Продольные силы NBРИГ= QАВ= –20 кН; NB= – FR=270 кН; NC= – FR–F1= –270–157= –427 кН; NA= – FR–F1–F2= –270–157–249= –676 кН; Эпюра продольных сил показана на рисунке 3.1, е. Проверкой правильности расчета служит: 1) равенство моментов в узле В, т.е. MBРИГ=MB (240 кН·м ≈ 242 кН·м); 2) равенство перепада эпюры моментов в точке С внешнему моменту, т.е. MCВ– MCН=М (113–6=107 кН·м = 107 кН·м); 3) равенство поперечных сил на верхней и нижней частях колонны, т.е. QАС= QАС (20 кН = 20 кН). |
