Прогиб сечения С
 Скачать 466 Kb. Скачать 466 Kb.
|
Прогиб сечения С
С. Пользуясь правилом Верещагина, вычисляем параметры эпюр 1 = -(1/2)4qa22a = -4qa3, 2 = 3 = (2/3)2qa22a = = 8qa3/3, C1 = (2/3)(-a) = -2a/3, C2 = C3 = (5/8)a и находим искомый прогиб
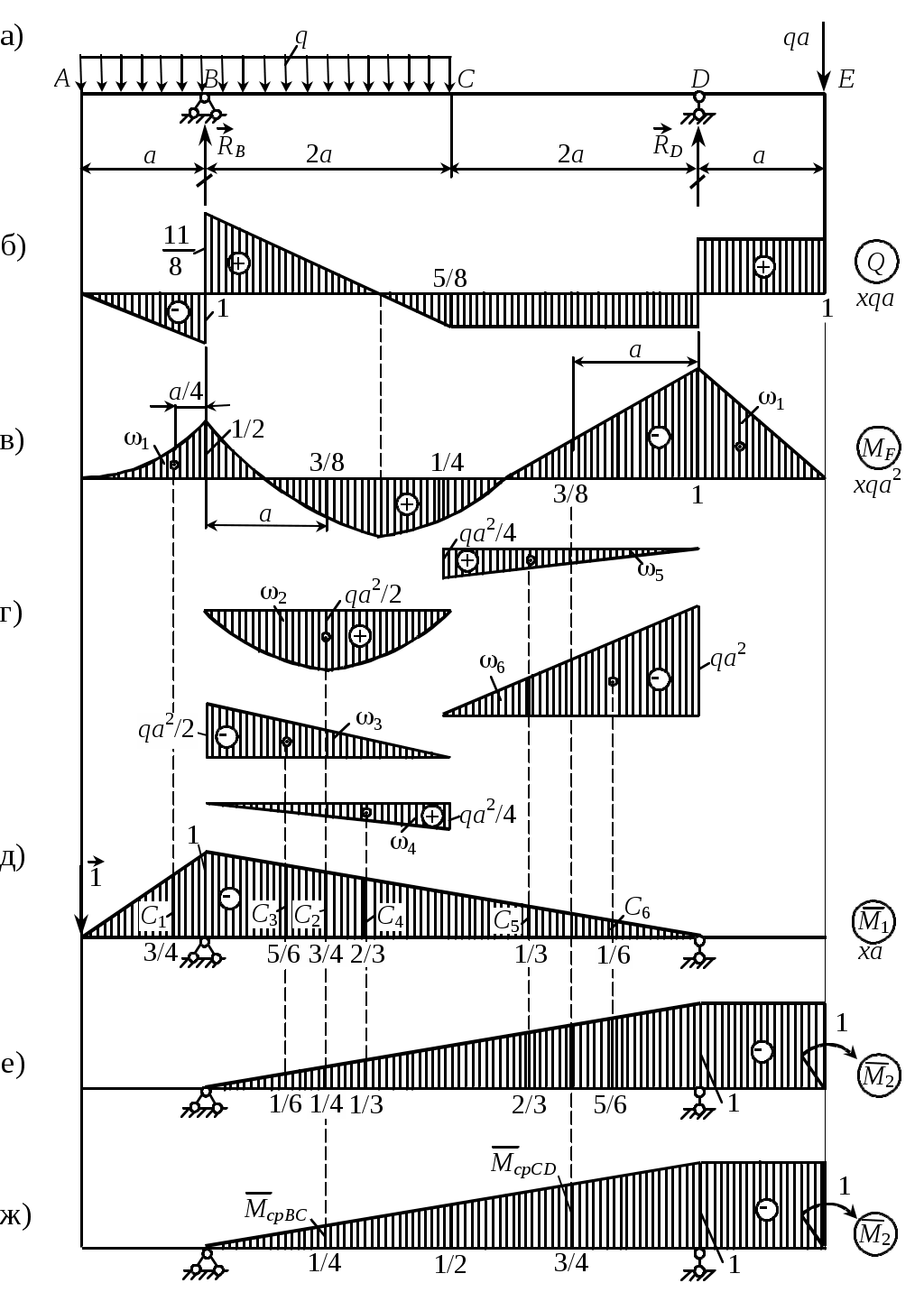
Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С. 2. Определение перемещений. Для вычисления интеграла Мора воспользуемся формулой Симпсона, последовательно применяя ее к каждому из трех участков, на которые разбивается балка. Участок АВ:  Участок ВС: 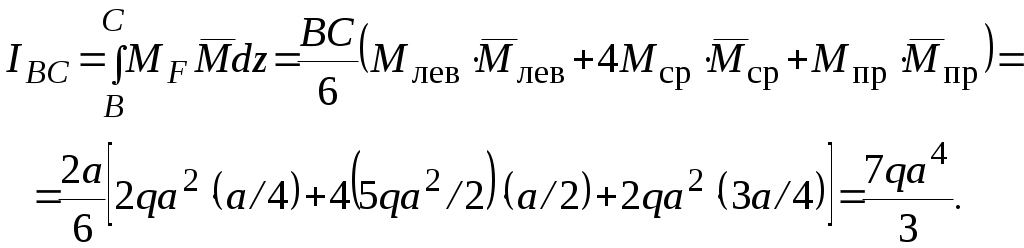 Участок СD: Искомое перемещение Пример 34. Определить прогиб сечения А и угол поворота сечения Е балки (рис. 55,а). Решение. 1. Построение эпюр изгибающих моментов. Эпюра МF (рис. 55,в). Определив опорные реакции mD = 0, RВ4a = q3a3,5а - qaa, RB = 19qa/8, Yi = 0, RD = 13qa/8, строим эпюры поперечной силы Q и изгибающего момента МF от заданной нагрузки. Эпюра Эпюра 2. Определение перемещений. Прогиб сечения А находим, пользуясь правилом Верещагина. Эпюру МF на участках ВС и CD разбиваем на простые части (рис. 55,г). Необходимые вычисления представляем в виде таблицы.
Получаем Знак “минус” в результате означает, что точка А перемещается не вниз, как была направлена единичная сила, а вверх. Угол поворота сечения Е находим двумя способами: по правилу Верещагина и по формуле Симпсона. По правилу Верещагина, перемножая эпюры MF и Для нахождения угла поворота по формуле Симпсона вычислим предварительно изгибающие моменты посредине участков: 
Искомое перемещение, увеличенное в EIx раз,
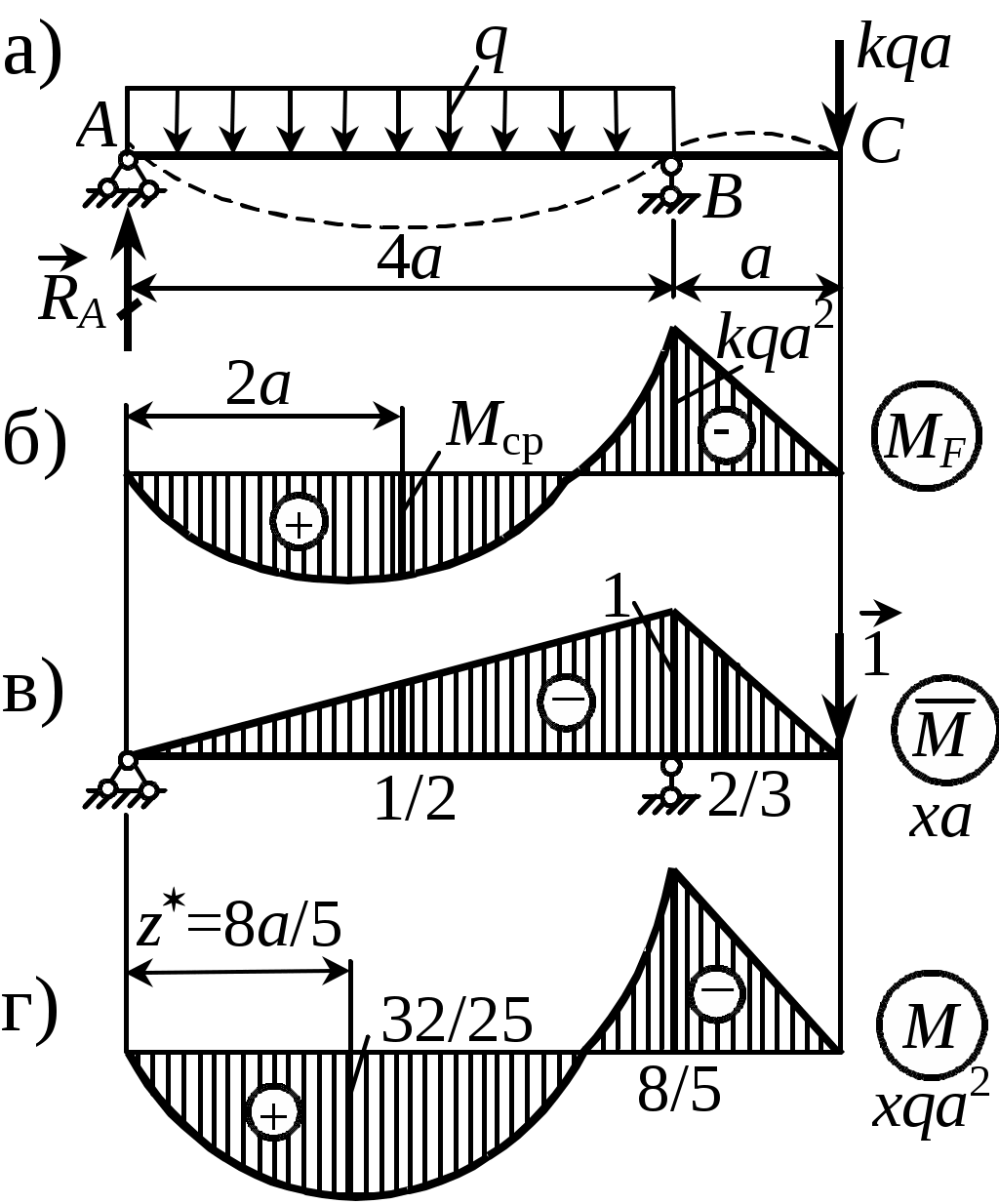
моментов от заданной нагрузки и от единичной силы, приложенной в сечении С, где ищется прогиб. По условию задачи VC = 0. С другой стороны, VC = Ii/(EIx). Интеграл на участке АВ вычисляем по формуле Симпсона, а на участке ВС – по правилу Верещагина. Находим предварительноПеремещение сечения С  Отсюда Отсюда При найденном значении k определяем значение опорной реакции в точке А: mB = 0, RA4a = q4a2a- (8/5)qa2, RA = (8/5)qa, исходя из которого находим положение точки экстремума на эпюре М согласно условию z = RA/q = (8/5)a. По значениям момента в характерных точках МА = МС = 0, МВ = -(8/5)qa2, строим эпюру изгибающего момента (рис. 56,г). |

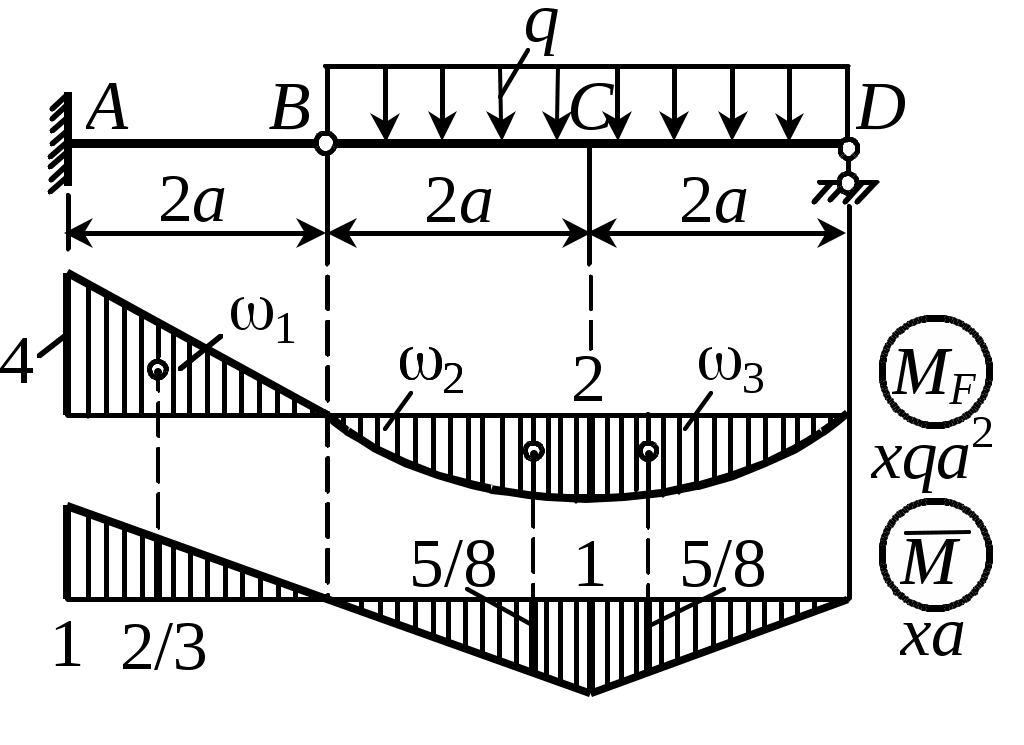
 Рис. 54
Рис. 54