Отчет, балка, Журавлёв. Расчет слабоискривленной балки
 Скачать 316.32 Kb. Скачать 316.32 Kb.
|
|
Санкт-Петербургский государственный политехнический университет Кафедра Компьютерные технологии в машиностроении Отчет Дисциплина: Механика контактного взаимодействия и разрушения Тема: Расчет слабоискривленной балки Студент гр. 23340/1 Журавлев А.С. Преподаватель Елисеев К.В. ________________2018 г. Санкт-Петербург 2018 Аналитическая справкаИсследуется слабоискривленная балка в условиях контактного взаимодействия с двумя ограничивающими ее абсолютно жесткими опорами, одна из которых сближается с другой. Нейтральная ось балки описывается полиномом (см. рис Рис. . Расчетная модель балки): 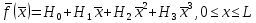 Задача симметрична относительно вертикальной оси, поэтому можно принять в рассмотрение только половину геометрической модели, наложив соответствующие условия симметрии, а именно ограничение горизонтального перемещения центральной точки и равенство нулю поворота балки в этой же точке. При нагружении каждое сечение балки имеет вертикальные перемещения 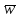 , угол поворота , угол поворота 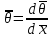 , момент внутренних сил , момент внутренних сил 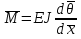 , перерезывающую силу , перерезывающую силу 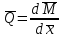 . .Вертикальное перемещение верхней опоры обозначим за 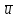 , оно изменяется от 0 до , оно изменяется от 0 до 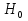 . .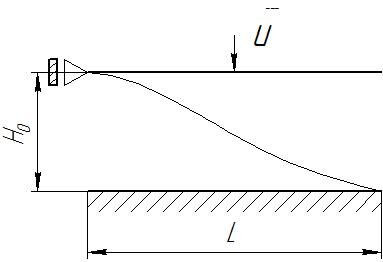 Рис. . Расчетная модель балки Можно перейти к безразмерным величинам. 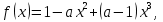 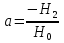 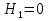 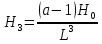 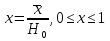 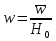 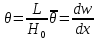 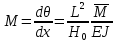 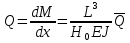 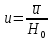 В заданном варианте задачи принимаются следующие параметры:
Рассмотрим балку с заданным параметром 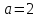 . .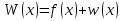 – уравнение нейтральной оси балки в актуальной конфигурации. – уравнение нейтральной оси балки в актуальной конфигурации.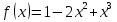 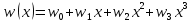 – вертикальные перемещения балки. – вертикальные перемещения балки.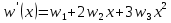 Условие симметрии ограничивает поворот балки при 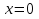 : :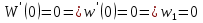 Тогда 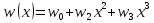 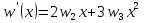 В верхней точке балки производная 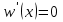 . Точек, в которых выполняется условие для этой производной, две. Точкой контакта балки с верхней опорой является крайняя левая, то есть . Точек, в которых выполняется условие для этой производной, две. Точкой контакта балки с верхней опорой является крайняя левая, то есть 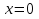 . Соответственно при всем нагружении эта точка остается точкой контакта, поэтому . Соответственно при всем нагружении эта точка остается точкой контакта, поэтому 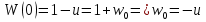 Тогда 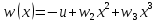 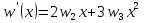 Другое граничное условие заключается в равенстве нулю момента на правом конце балки: 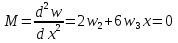 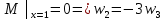 Тогда 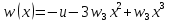 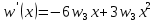 Последнее граничное условие заключается в равенстве нулю 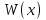 в точке контакта с нижней опорой. При этом в точке контакта с нижней опорой. При этом 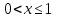 . .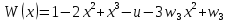 В результате решения можно получить диаграмму состояний в зависимости от различных параметров 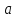 , приведенную на рис. Рис. . , приведенную на рис. Рис. .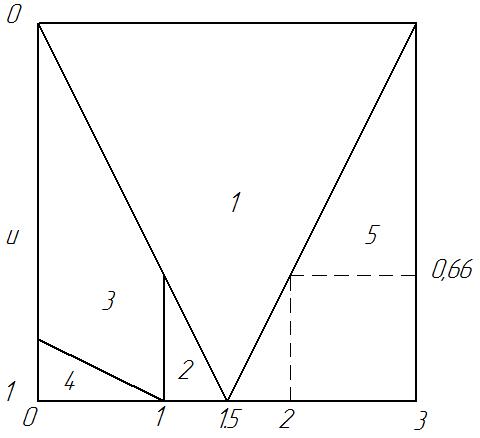 Рис. . Диаграмма состояний, показывающая зависимость конфигурации контактных точек от параметра а и перемещения u Из этой диаграммы видно, что при параметре 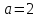 при при 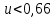 контактные точки конфигурированы в соответствии с конфигурацией 1. Эта конфигурация совпадает с ненагруженным состоянием: верхняя точка контакта при контактные точки конфигурированы в соответствии с конфигурацией 1. Эта конфигурация совпадает с ненагруженным состоянием: верхняя точка контакта при 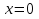 и нижняя точка контакта при и нижняя точка контакта при 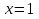 . С дальнейшим увеличением . С дальнейшим увеличением 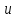 система приходит в конфигурацию 5 (рис. Рис. .) система приходит в конфигурацию 5 (рис. Рис. .)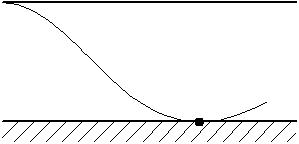 Рис. . Конфигурация 5 контактных точек Ход работыРасчет производится с помощью макроса. Посредством создания кубического сплайна по точкам создается геометрическая модель балки. После задания механических свойств и сечения балки создаются контактные пары, в которых опоры являются абсолютно жесткими телами. Производится решение задачи и постпроцессинг. Вводится псевдовремя 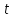 , которое изменяется от 0 до 1. , которое изменяется от 0 до 1. 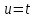 График зависимости силы реакции 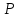 от перемещения верхней опоры представлен на рисунке Рис. . Если мы заменим перемещения от перемещения верхней опоры представлен на рисунке Рис. . Если мы заменим перемещения 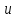 на соответствующую силу прижатия, то эта сила и сила на соответствующую силу прижатия, то эта сила и сила 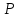 будут равны по модулю в соответствии со вторым законом Ньютона применительно ко всей системе. Из графика видно, что в начале нагружения сила прижатия имеет линейный вид зависимости от будут равны по модулю в соответствии со вторым законом Ньютона применительно ко всей системе. Из графика видно, что в начале нагружения сила прижатия имеет линейный вид зависимости от  , поэтому можно аппроксимировать ее линейной функцией. Тангенс угла наклона этой функции равен 306,7 в безразмерных координатах. Если придать размерность перемещениям, то тангенс станет равен 30670 Н/м. , поэтому можно аппроксимировать ее линейной функцией. Тангенс угла наклона этой функции равен 306,7 в безразмерных координатах. Если придать размерность перемещениям, то тангенс станет равен 30670 Н/м.Рис. . График зависимости силы реакции от перемещения верхней опоры  , а также линейная аппроксимация линейного участка графика силы реакции , а также линейная аппроксимация линейного участка графика силы реакцииИсследуем зависимость расположения точек контакта от перемещения  . Для этого приведем картины распределения контактных напряжений и статуса контакта в различные моменты времени. . Для этого приведем картины распределения контактных напряжений и статуса контакта в различные моменты времени.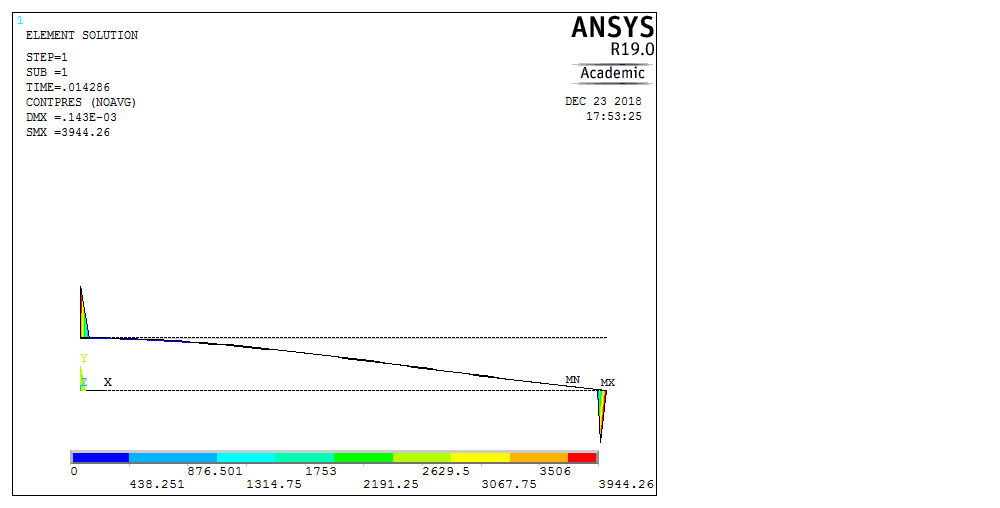 Рис. . Распределение контактных напряжений при t = 0.01 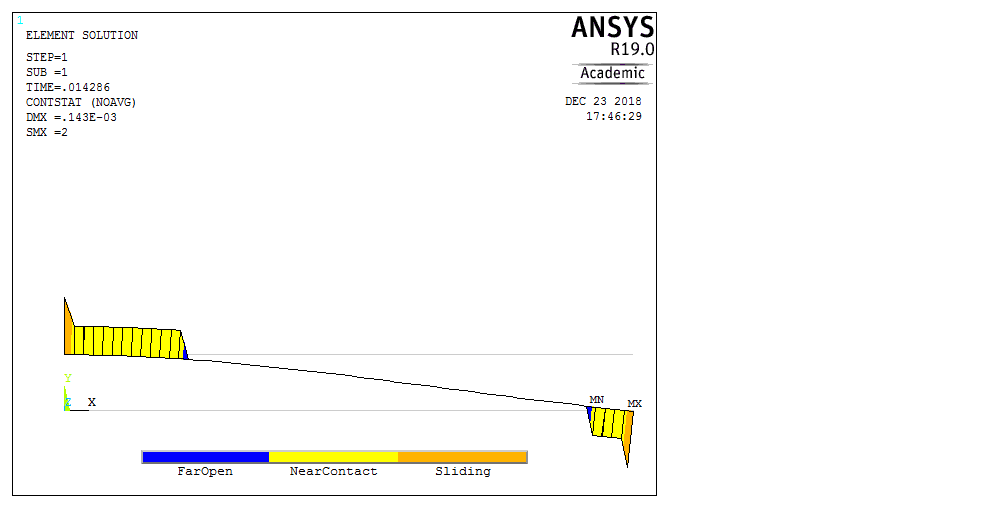 Рис. . Распределение контакта при t = 0.01 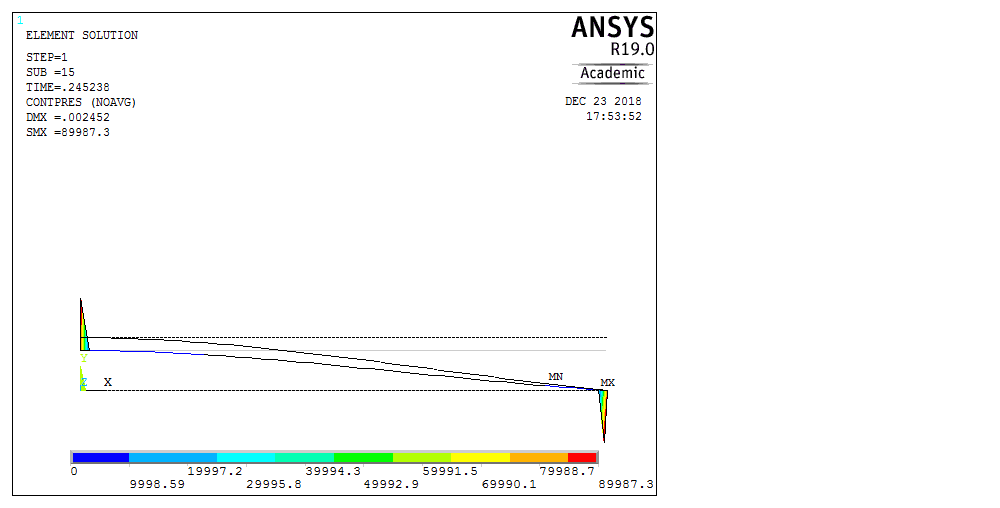 Рис. . Распределение контактных напряжений при t = 0.25 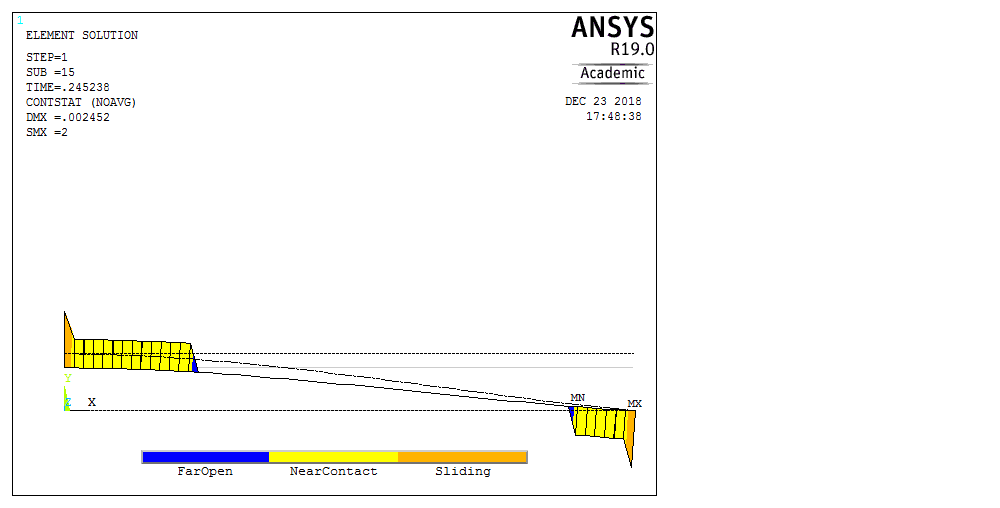 Рис. . Распределение контакта при t = 0.25 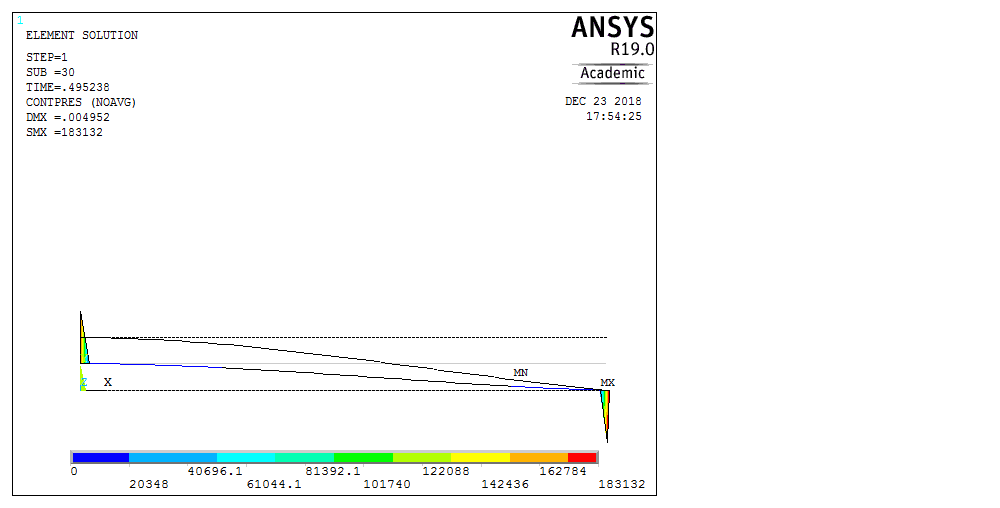 Рис. . Распределение контактных напряжений при t = 0.5 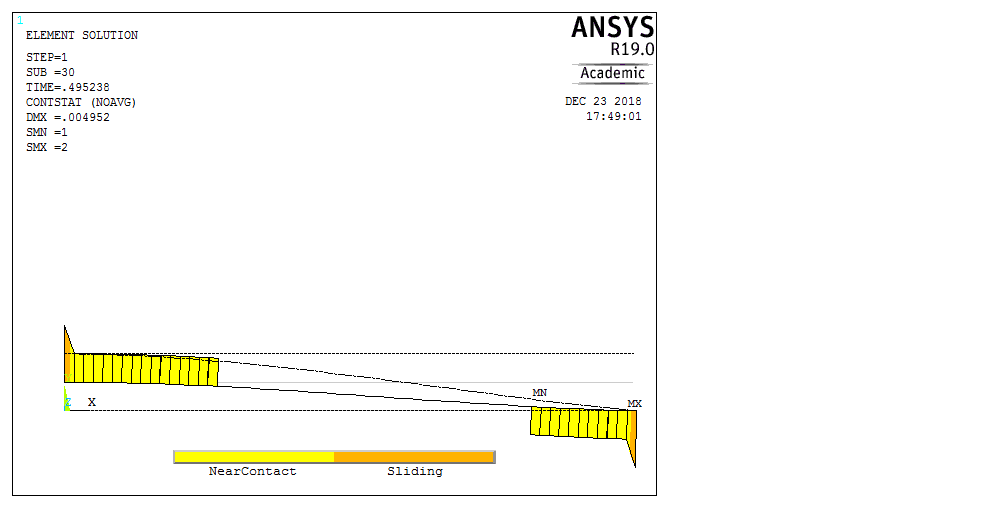 Рис. . Распределение контакта при t = 0.5 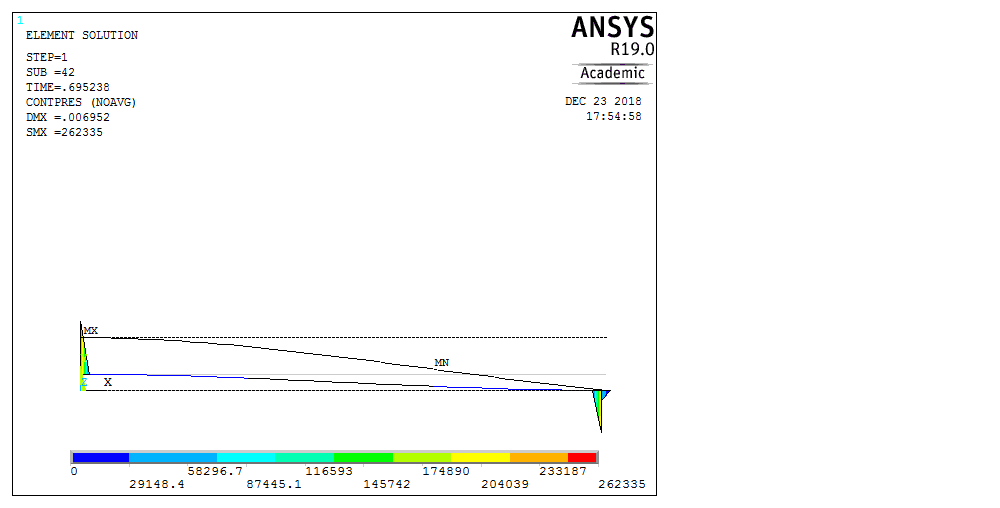 Рис. . Распределение контактных напряжений при t = 0.7 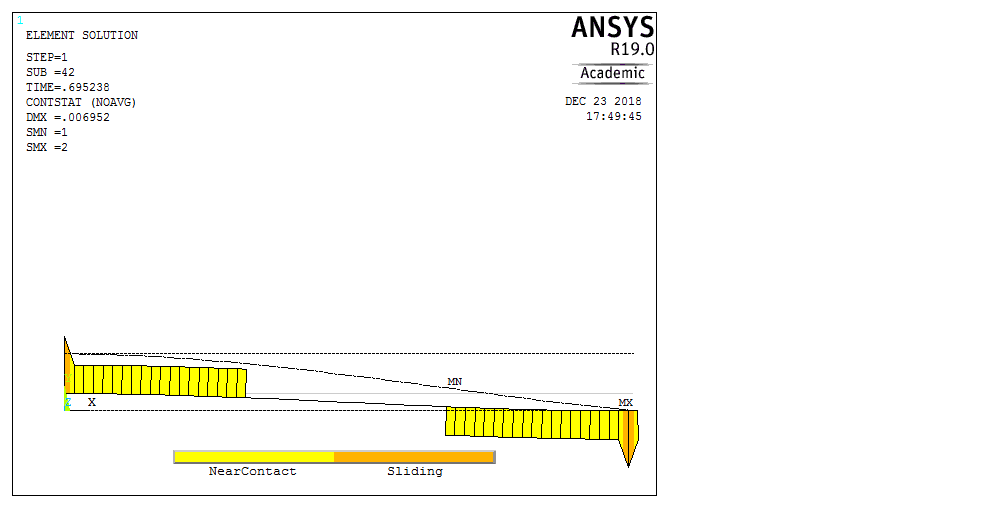 Рис. . Распределение контакта при t = 0.7 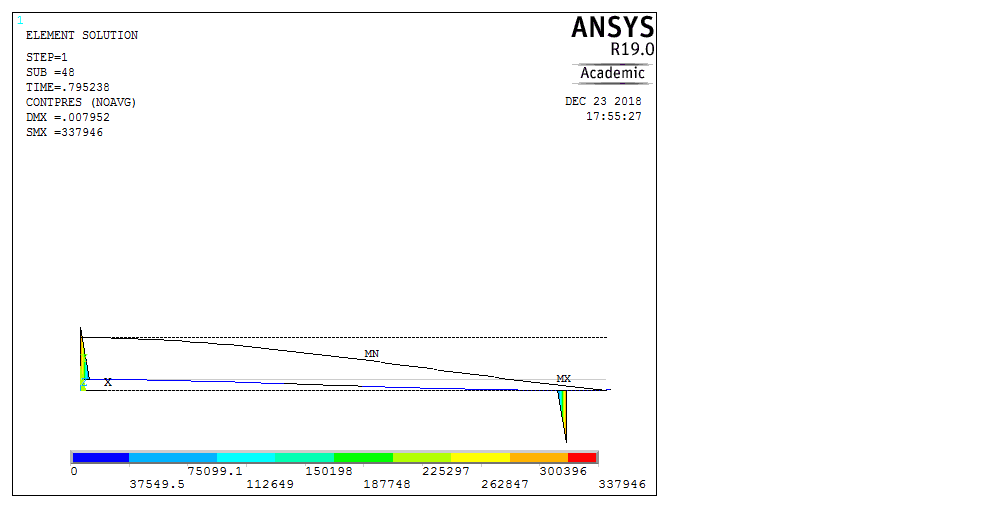 Рис. . Распределение контактных напряжений при t = 0.8 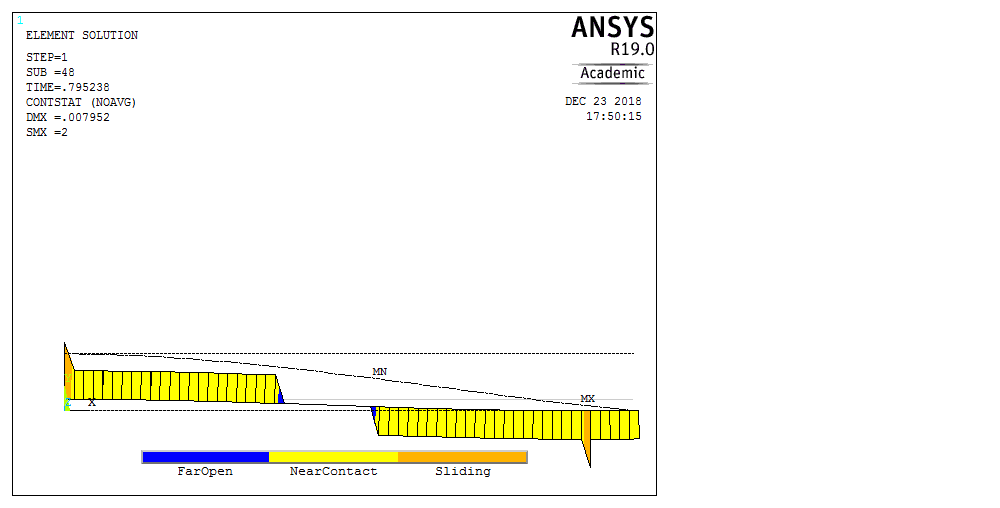 Рис. . Распределение контакта при t = 0.8 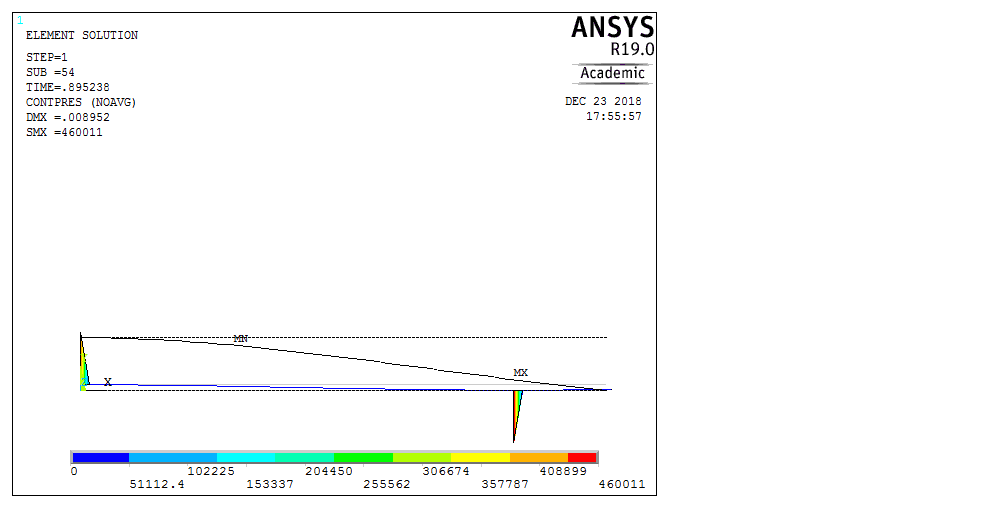 Рис. . Распределение контактных напряжений при t = 0.9 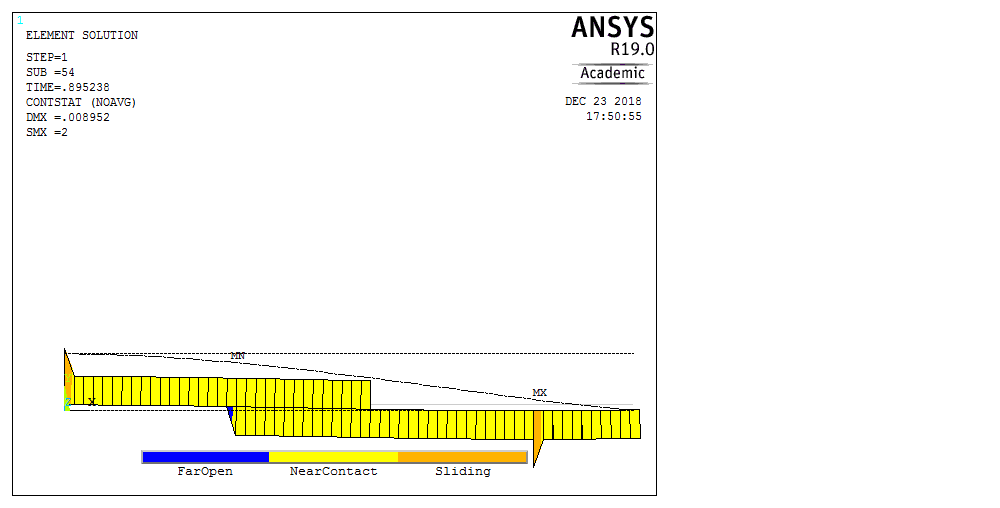 Рис. . Распределение контакта при t = 0.9 Отсюда видно, что контакт балки с верхней опорой при всем нагружении содержит только одну точку контакта, расположенную в 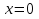 . Точка контакта балки с нижней опоры остается одной. Видно, что до значения . Точка контакта балки с нижней опоры остается одной. Видно, что до значения  сохраняется конфигурация 1. При дальнейшем нагружении система переходит в конфигурацию 5, что соответствует аналитическому решению, когда такое отклонение происходит при сохраняется конфигурация 1. При дальнейшем нагружении система переходит в конфигурацию 5, что соответствует аналитическому решению, когда такое отклонение происходит при  . Из графиков на рис. Рис. видно, что отклонение от линейной зависимости прижимающей силы от перемещений при численном анализе происходит при значении 0,67. Можно предположить, что переход из конфигурации 1 в конфигурацию 5 может сопровождаться потерей линейности зависимости прижимающей силы от перемещений опоры, то есть балка в конфигурации 1 может быть рассмотрена как пружина с жесткостью 30670 Н/м при данном сечении и данном параметре . Из графиков на рис. Рис. видно, что отклонение от линейной зависимости прижимающей силы от перемещений при численном анализе происходит при значении 0,67. Можно предположить, что переход из конфигурации 1 в конфигурацию 5 может сопровождаться потерей линейности зависимости прижимающей силы от перемещений опоры, то есть балка в конфигурации 1 может быть рассмотрена как пружина с жесткостью 30670 Н/м при данном сечении и данном параметре 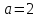 . .ВыводыВ ходе работы с помощью ANSYS APDL была решена контактная задача о деформации слабоискривленной балки, находящейся между двумя абсолютно жесткими плоскими опорами. Представлен график зависимости силы реакции от перемещения (см. рис. Рис. . График зависимости силы реакции от перемещения верхней опоры , а также линейная аппроксимация линейного участка графика силы реакции). Помимо этого, проведена линейная аппроксимация начального участка графика зависимости прижимающей силы от перемещений опоры. Сделано предположение, что конфигурация 1 расположения контактных точек соответствует пружине с коэффициентом жесткости 30670 Н/м при данном значении 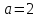 и заданном сечении балки. и заданном сечении балки.Из графиков распределения контактных напряжений и пятна контакта видно, что при значениях 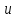 , близких к 0,7 происходит переход точек контакта из конфигурации 1 в конфигурацию 5, что соответствует аналитическому решению. , близких к 0,7 происходит переход точек контакта из конфигурации 1 в конфигурацию 5, что соответствует аналитическому решению. |

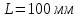 ;
;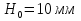 ;
;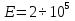 МПа;
МПа;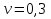 ;
;