Расчет статически неопределимых систем
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
 Министерство образования Российской Федерации Санкт-Петербургский государственный горный институт им. Г.В. Плеханова (технический университет)  Расчетно-графическое заданиеПо дисциплине: Сопротивление материалов(наименование учебной дисциплины согласно учебному плану) Тема: Расчет статически неопределимых систем.Выполнил: студент гр. -02 ______________ /./ (подпись) (Ф.И.О.) ОЦЕНКА: _____________ Дата: __________________ ПРОВЕРИЛ:Руководитель: П. ____________ /./(должность) (подпись) (Ф.И.О.) Санкт-Петербург 2004 год. Цель задания: расчет статически неопределимой системы в условиях работы составляющих ее элементов в режиме растяжения-сжатия (одноосное напряженное состояние). Система называется статически неопределимой, если для определения усилий в ее элементах недостаточно уравнений равновесия статики, т.е. число неизвестных внутренних усилий (реакций) больше, чем число уравнений равновесия статики. Степень статической неопределимости системы: К=R-Y, где К - степень статической неопределимости системы; R - число неизвестных внутренних усилий (реакций); Y - число уравнений равновесия статики. Исходные данные (вариант №3): Схема стержневой системы: 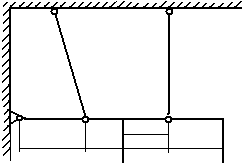 Рис.1 Материалы стержней: 1 - сталь, 2 - сталь; упругие модули на растяжение (сжатие): Е1=Е2= 1) Определение усилий от внешней силы Р ( Вычертим расчетную схему балки с указанием всех размеров. Для расчета усилий используем метод сечений. Сечения проведем через оба стержня. Рассмотрим равновесие нижней части системы, заменяя действие отбрасываемой верхней части стержней внутренними усилиями реакций R1,R2. 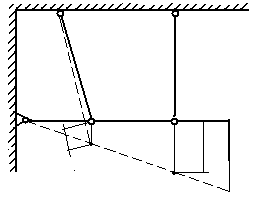 Рис.2 Составим уравнения статики: или Остальные уравнения статики можно не составлять, так как они необходимы лишь при определении реакций в шарнире XA,YA, чего не требуется по условию задачи. Таким образом, степень статической неопределимости системы К=1, так как мы имеем два неизвестных усилия R1,R2 и одно уравнение равновесия статики. Для составления одного уравнения совместности деформаций необходимо рассмотреть схему перемещений системы. Под действием внешней силы Р1 первый стержень удлинится на величину Удлинения Уравнения совместимости деформаций в данном случае проще всего составить, воспользовавшись подобием треугольников АВВ2 и АСС1: Из треугольника ВВ1В2 определим Подставив равенства (5) в формулу (4), получим уравнение совместности деформаций заданной стержневой системы или где из уравнения (6) получим: Учитывая, что Далее решаем совместно систему уравнений (3) и (7): 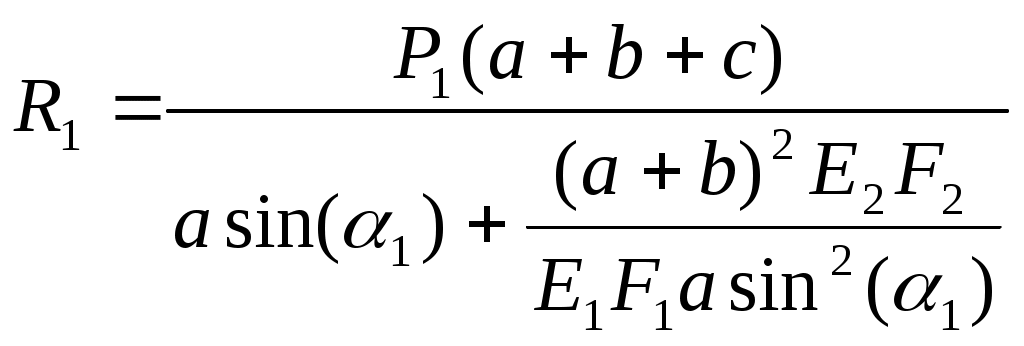 ; ; 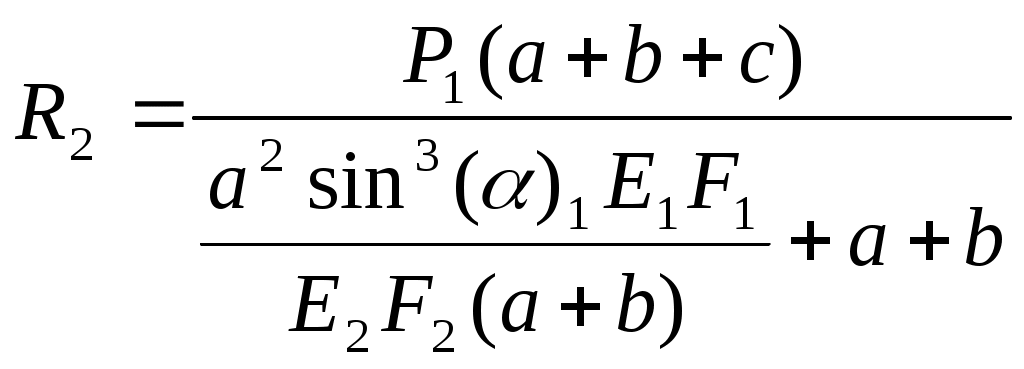 (8) (8)Из выражений (8) при известном отношении F1/F2 находим численные значения усилии: R1= R2= Проверка правильности найденных численных значений производится путем подстановки R1= 2) Определение напряжений, вызванных неточностью изготовления (Р=0, Первый стержень изготовлен с неточностью 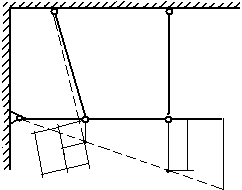 Рис.3 Уравнение равновесия для рассматриваемого случая будет иметь следующий вид: Для перемещений получим Соотношение между Подставив выражения (10) в равенство (11), получим уравнение совместности деформаций: Выразив согласно закону Гука удлинения Перейдем в уравнении (13) к новым переменным, в качестве которых выберем напряжения Тогда, выразив Перепишем уравнение (9) в напряжениях: или Решим систему уравнений (14) и (15) относительно неизвестных напряжений: 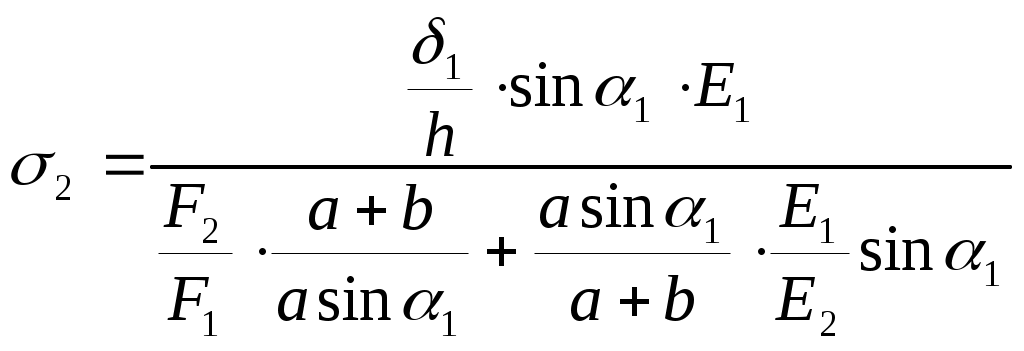 = =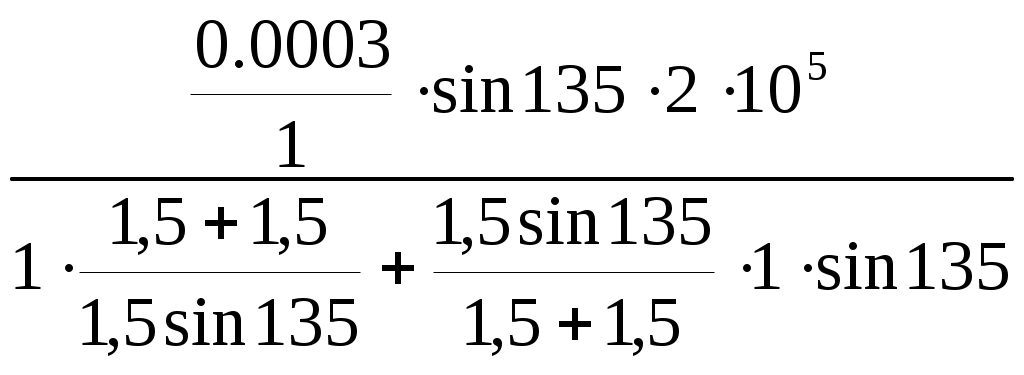 =-13,8МПа =-13,8МПа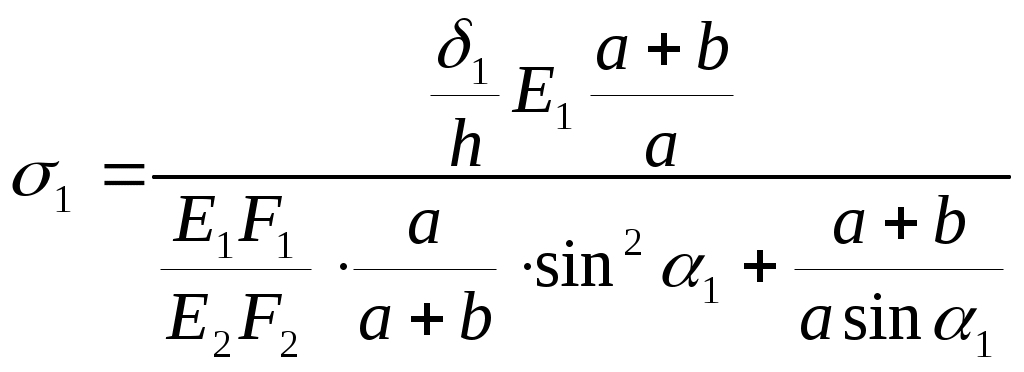 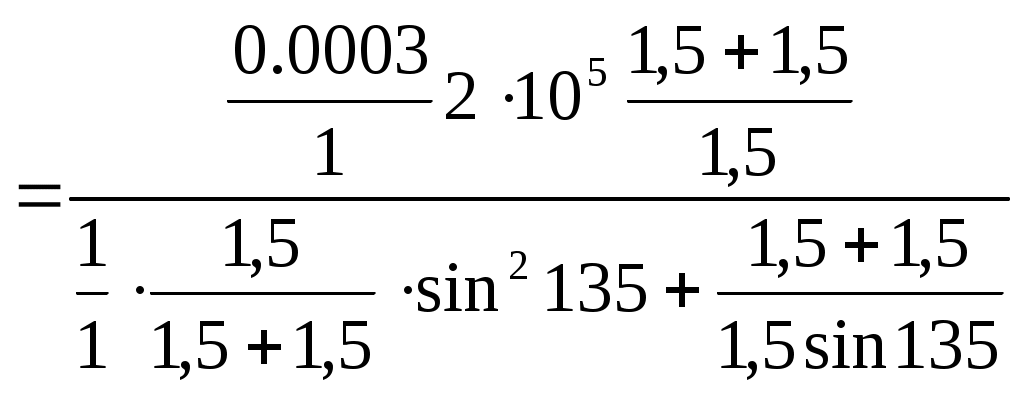 =39МПа (16) =39МПа (16) При заданных величинах 3) Расчет температурных напряжений (Р=0, 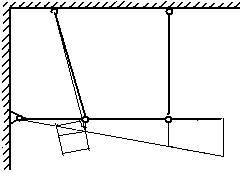 Первый стержень системы нагрет до температуры Уравнение равновесия имеет следующий вид: Для перемещений получим Соотношение между Подставив выражения (18) в равенство (19), получим уравнение совместности деформаций: Выразив согласно закону Гука удлинения Перейдем в уравнении (21) к новым переменным, в качестве которых выберем напряжения Тогда, выразив Перепишем уравнение (9) в напряжениях: или Решим систему уравнений (22) и (23) относительно неизвестных напряжений: 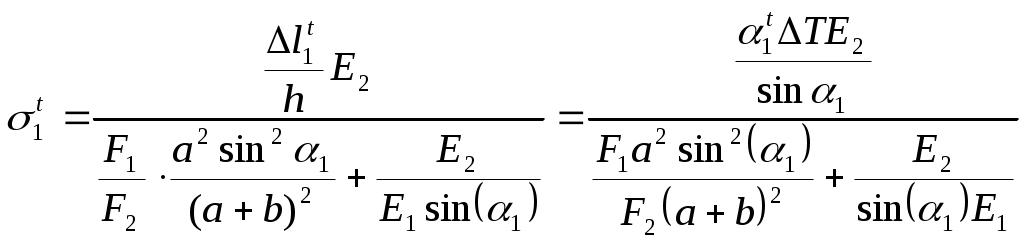 ; ;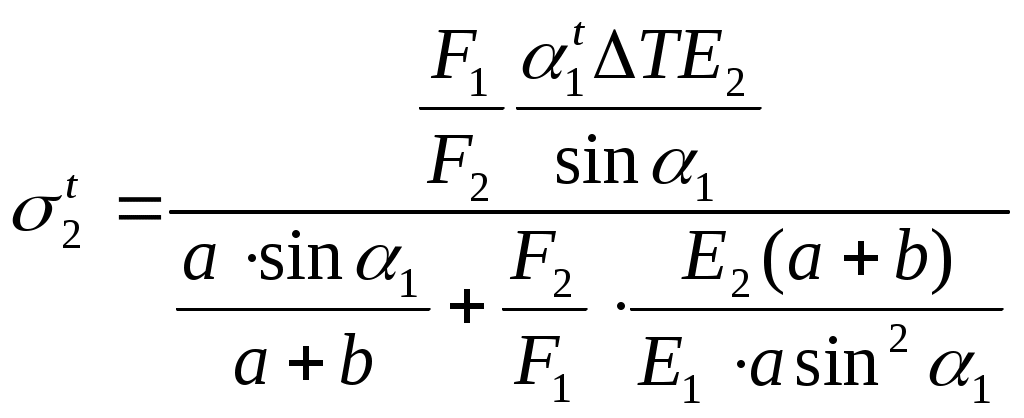 (24) (24)При 4) Подбор сечений элементов системы. При расчете сечений учитывается одновременное действие всех нагружающих факторов: внешней нагрузки, внутренних монтажных и температурных напряжений. Полученные в пп.1,2,3 данные представлю в виде таблицы:
Условия прочности для каждого из стержней записывается в виде неравенств Отсюда Подставив значения из таблицы в формулы (26), получу Из выбранных численных значений для Учитывая заданное отношение Выбираем: | |||||||||||||
