Прикл мех 8887986. Задача 1 растяжение и сжатие стержней для заданной шарнирно стержневой системы требуется
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
|
СОДЕРЖАНИЕ Задача 1………………………………………………..……………………..…..3 Задача 2………………………………………………..…………………………6 Задача 3………………………………………………..……………………..…..9 Задача 4………………………………………………..……………………..…15 Список использованной литературы ………………….……………………..19 ЗАДАЧА № 1 РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ Для заданной шарнирно – стержневой системы требуется: Проверить прочность растянутого (сжатого) стержня АВ (материал – сталь Ст3) указанного поперечного сечения по нормальным напряжениям, если Подобрать сечение стержня АВ (материал – сталь Ст3) в виде равнополочного уголка из условия наименьшего расхода материала, если Определить удлинение (укорочение) подобранного растянутого (сжатого) стержня АВ, если Исходные данные: Решение: Стержень АВ шарнирно стержневой системы работает на растяжение или сжатие. 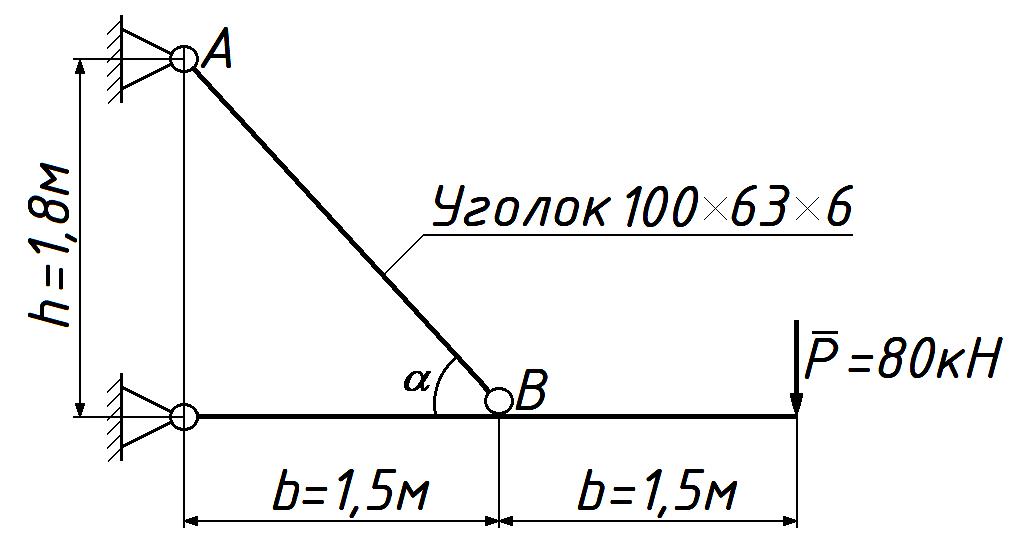 Рисунок 1 – Схема шарнирно - стержневой системы Определяем продольную силу в стержне, используя метод сечений. Рассечем стержень АВ поперечным сечением 1-1 в произвольном месте. Заменим действие отброшенной части на оставшуюся внутренним усилием, предполагая, что стержень растянут. 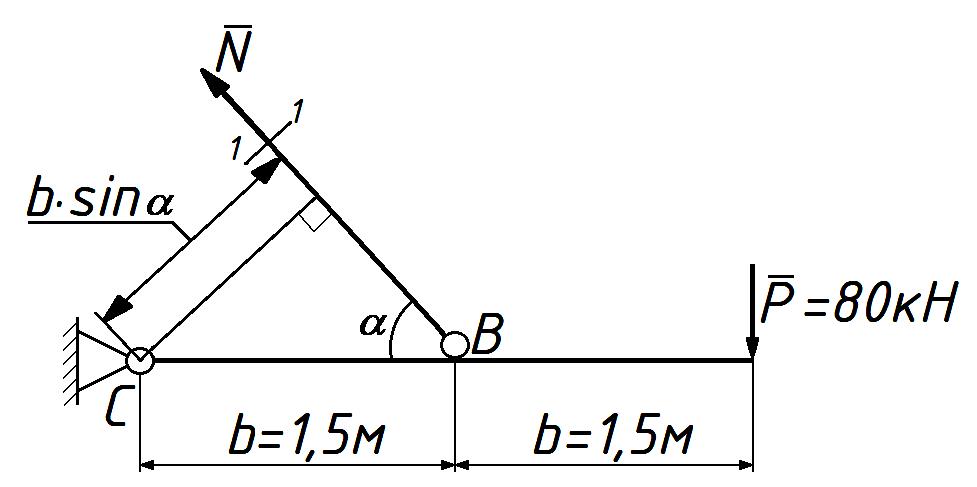 Рисунок 2 – Расчетная схема шарнирно-стержневой системы Определим значение угла 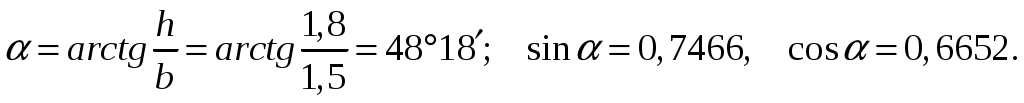 Составим уравнение моментов сил относительно точки (опоры) 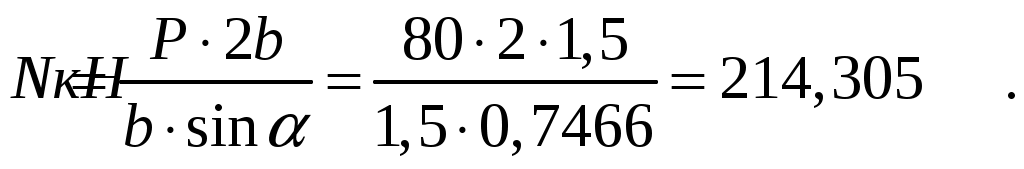 Знак «+» показывает, что сила N направлена от сечения 1-1, то есть стержень АВ растягивается. Площадь поперечного сечения стержня АВ найдем по ГОСТ8510-86 (уголок стальной горячекатаный неравнополочный): По условию задачи Абсолютное значение наибольшего нормального напряжения в стержне АВ: 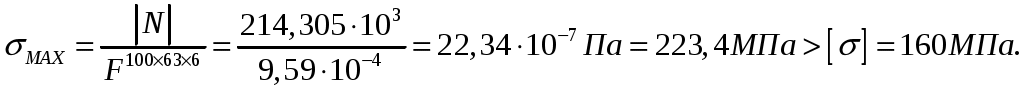 Условие прочности не выполняется. Определим требуемую для выполнения условия прочности площадь поперечного сечения стержня АВ: 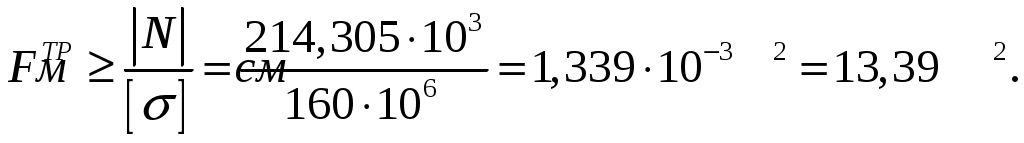 По ГОСТ8509-93 (уголки стальные горячекатаные равнополочные) выберем уголок с ближайшей большей площадью поперечного сечения. Это - равнополочный уголок Абсолютное значение наибольшего нормального напряжения в стержне АВ: 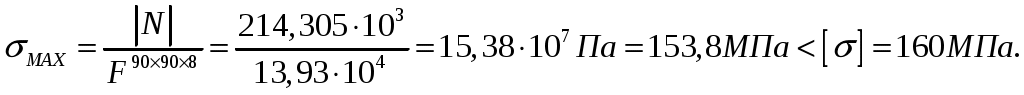 Условие прочности выполняется. Коэффициент запаса прочности элементов конструкций из пластичных материалов определяется по отношению к пределу текучести 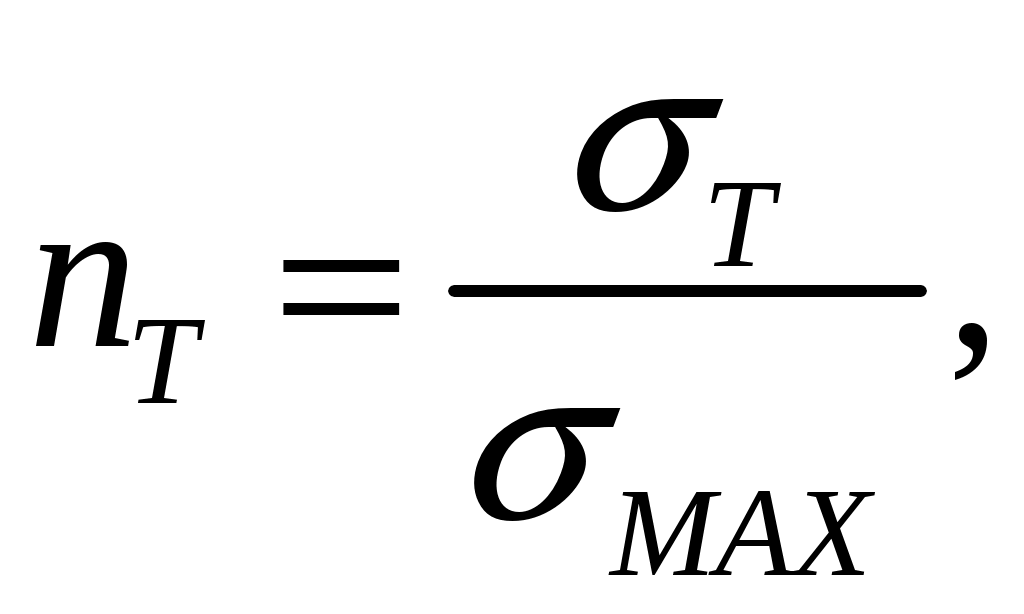 где Тогда для стержня АВ с сечением в виде уголка 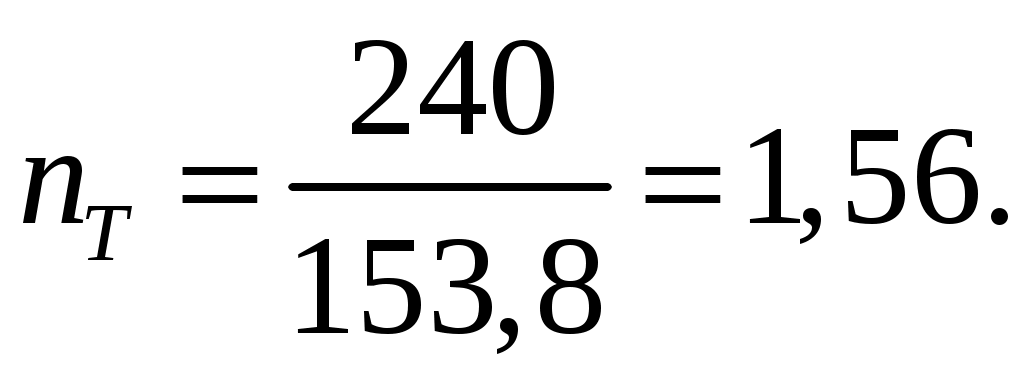 Величина Абсолютное удлинение (укорочение) стержня при растяжении (сжатии) определяем по закону Гука: где 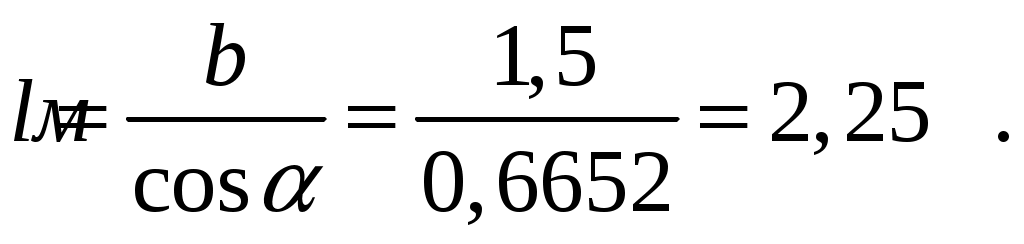 Удлинение стержня АВ в виде уголка 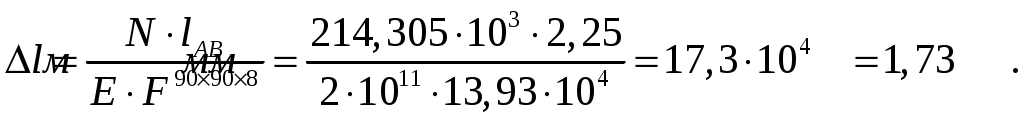 Стержень удлиняется на ЗАДАЧА № 2 ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ Для заданного поперечного сечения требуется: Вычертить сечение в масштабе 1:1 на листе формата А4 и показать основные размеры. Определить положение центра тяжести. Определить положение главных осей инерции. Вычислить главные моменты инерции. Показать на чертеже положение центра тяжести, главных осей инерции и все расстояния, полученные расчетным путем. Данные для расчета: Двутавровая балка № 12; Равнополочные уголки Решение: Сечение является сложным, так как состоит из трех простых сечений. Первый – двутавровая балка № 12, второй и третий – равнополочные уголки Выбираем из сортамента геометрические элементы простых сечений. Двутавровая балка № 12 ГОСТ8239-89: Равнополочные уголки Вычертим сечение бруса на листе формата А4 в масштабе 1:1 и показываем основные размеры. Составное сечение имеет вертикальную ось симметрии У, которая совпадает с осью У1 двутавра. Следовательно, центр тяжести сечения лежит на оси У, а ось У является одной из двух главных осей инерции всего сечения. Чтобы найти положение другой главной оси Z, нужно определить место центра тяжести составного сечения на оси У. Определим расстояния от вспомогательной оси ZВСП до центра тяжести каждого простого сечения  Рисунок 3 – Чертеж составного сечения Расстояние от вспомогательной оси ZВСП до центра тяжести составного сечения по высоте определяется формулой 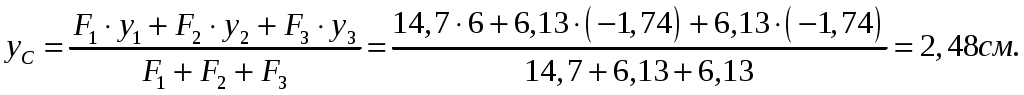 Главные моменты инерции составного сечения Определим расстояния от осей главных до осей каждого простого сечения Моменты инерции составного сечения относительно главных осей Z и У. 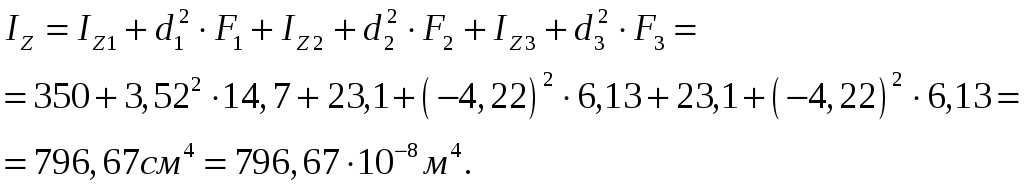 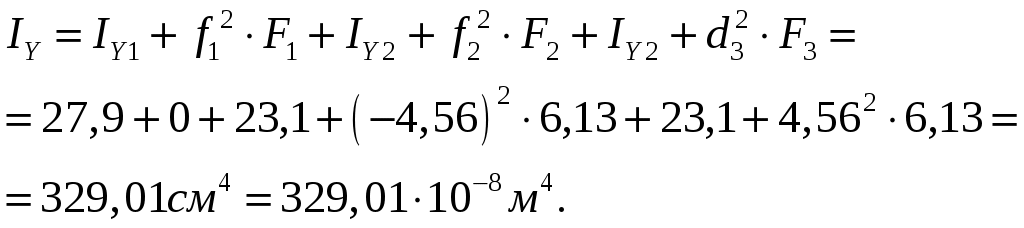 ЗАДАЧА № 3 ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ БАЛОК Для заданных балок требуется: Построить эпюры внутренних усилий с вычислением значений сил и изгибающих моментов в характерных сечениях балок. Проверить прочность консольной балки (материал – сталь Ст3) поперечного сечения по нормальным напряжениям, если Для двухопорной балки (материал – сталь Ст3) подобрать поперечное сечение в форме двутавра из условия прочности по нормальным напряжениям, если Вычислить коэффициент запаса прочности по отношению к пределу текучести, если Данные для расчета: 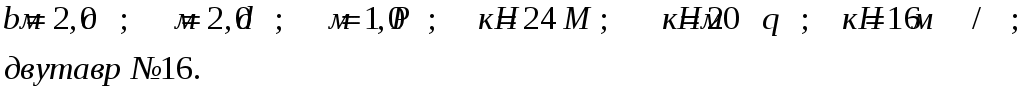 Расчет консольной балки: Балка имеет два участка, различающихся характером нагружения, а следовательно, и законы изменения поперечных сил и изгибающих моментов.  Рисунок 4 – Схема консольной балки Зададимся системой координат, совместив ось Х с продольной осью балки, а оси У и Z с главными центральными осями инерции поперечного сечения. Расчет ведем от свободного конца, тогда не потребуется определять опорные реакции заделки. Проведем характерные сечения и находим внутренние усилия в этих сечениях. На участке действия равномерно распределенной нагрузки эпюра изгибающих моментов представляет собой ветвь параболы, экстримум которой находится в сечении 5-5, где эпюра Q пересекает свою ось. Определим ординату сечения 5-5 из уравнения 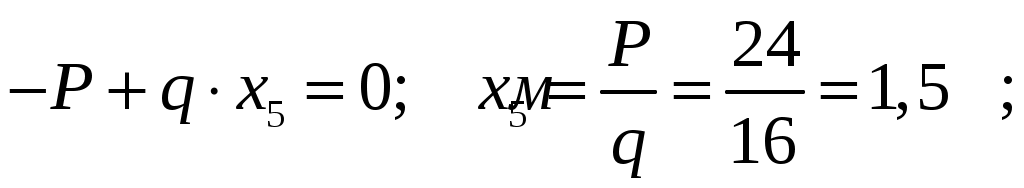 По вычисленным значениям строим эпюры внутренних усилий. 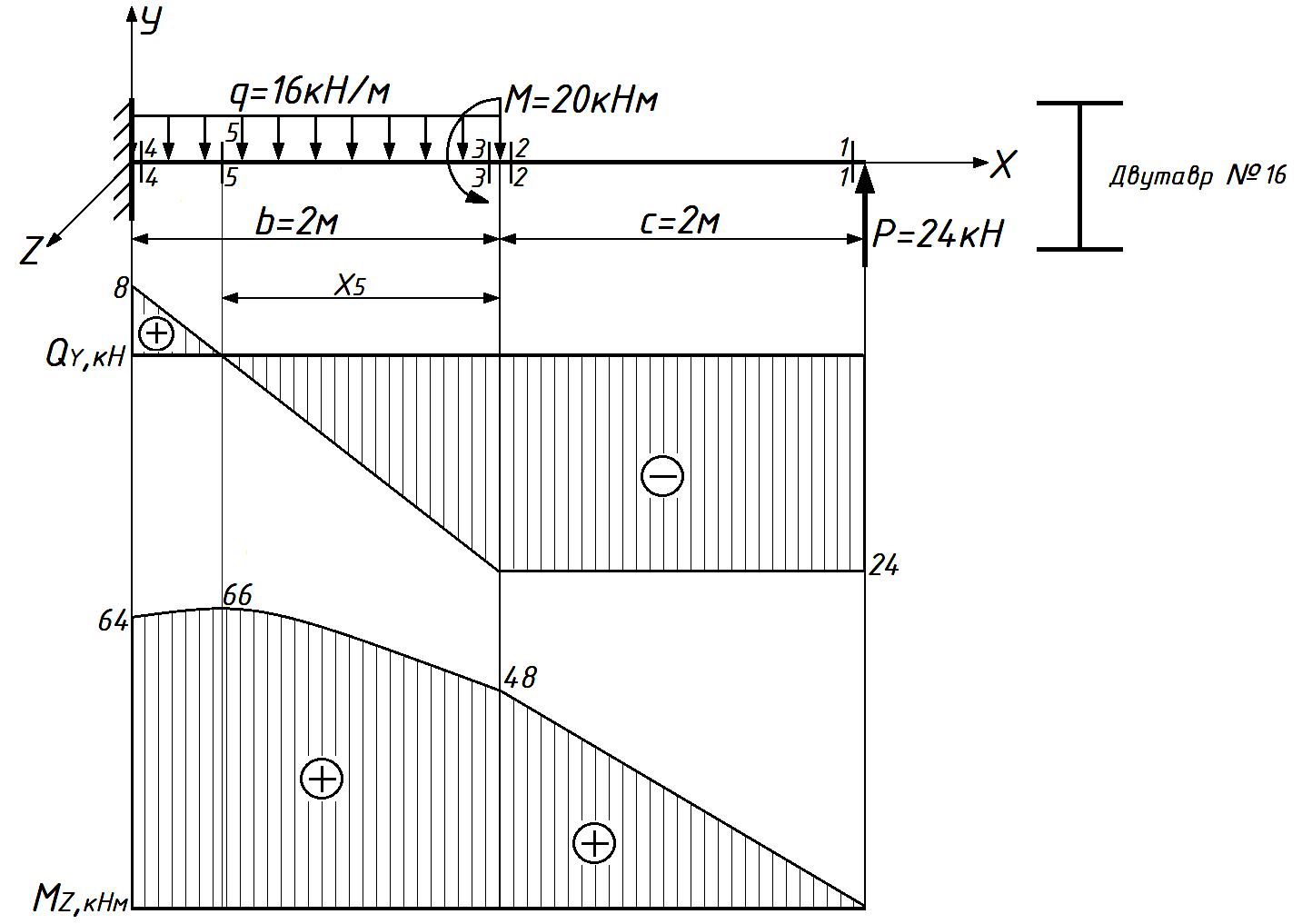 Рисунок 5 – Расчетная схема консольной балки и эпюры внутренних усилий Условие прочности по нормальным напряжениям при прямом изгибе для балок из пластичных материалов имеет вид: 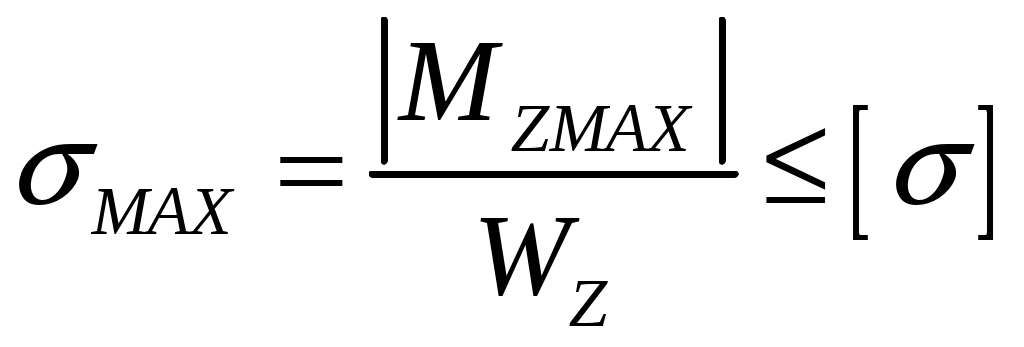 , ,где Определим абсолютное значение наибольшего нормального напряжения в опасном сечении балки и сравним его с допускаемым 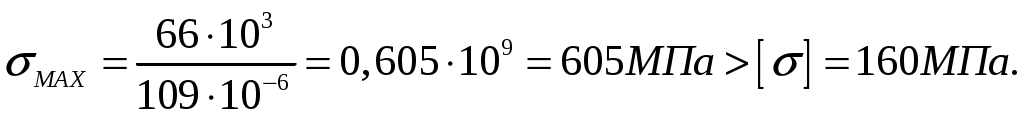 Условие прочности не выполняется. Необходимо принять двутавр не менее № 30, для которого 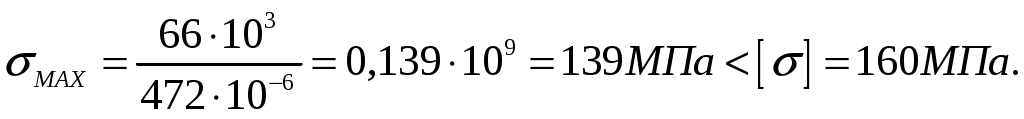 Расчет двух опорной балки Двух опорная балка имеет три участка, различающихся характером нагружения, а следовательно, и законами изменения поперечных сил и изгибающих моментов.  Рисунок 6. – Схема двух опорной балки Зададимся системой координат, совместив ось Х с продольной осью балки, а оси У и Z с главными центральными осями инерции поперечного сечения. О  пределим опорные реакции. Отбросим опоры А и В и заменим их действие на балку вертикальными составляющими реакций VA и VB (горизонтальная составляющая в опоре А равна нулю, так как внешние горизонтальные нагрузки отсутствуют). пределим опорные реакции. Отбросим опоры А и В и заменим их действие на балку вертикальными составляющими реакций VA и VB (горизонтальная составляющая в опоре А равна нулю, так как внешние горизонтальные нагрузки отсутствуют).Рисунок 7. – Расчетная схема двухопорной балки Составим уравнения равновесия:   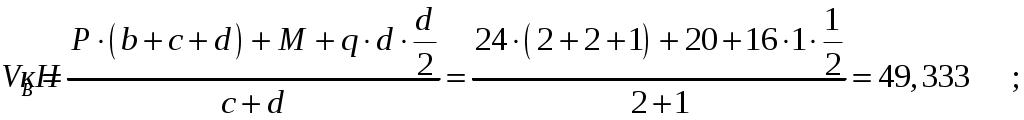 Для проверки правильности полученных результатов составим третье уравнение равновесия, спроецировав все силы на ось У: Опорные реакции найдены верно. Проведем характерные сечения и находим внутренние усилия в этих сечениях. 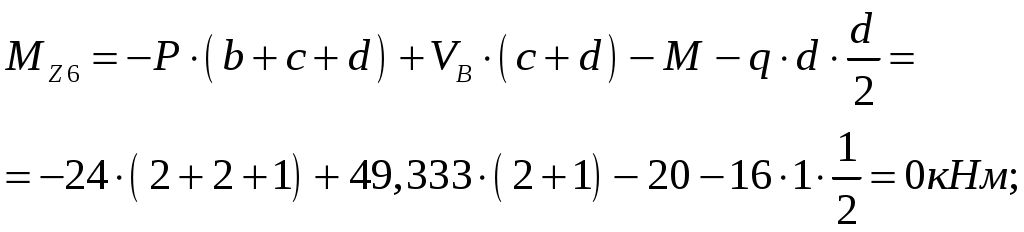 По вычисленным значениям построим эпюры внутренних усилий. Опасными сечениями балки являются сечения 2-2 и 3-3.В них действует наибольший по абсолютному значению изгибающий момент Подбираем двутавровую балку из условия прочности определив момент с противления сечения изгибу при заданном нормальным напряжении 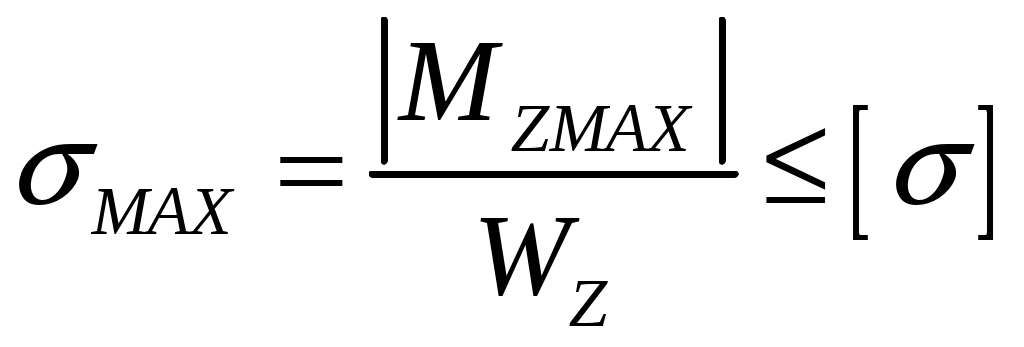 , откуда , откуда 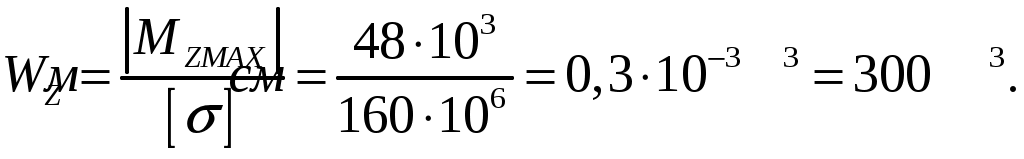 По ГОСТ8239-89 выбираем двутавр № 27 с ближайшим большим моментом сопротивлении Вычислим абсолютное значение наибольшего нормального напряжения в опасных сечениях балки 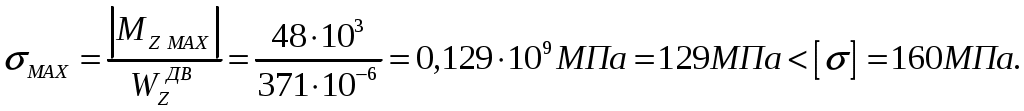 Условие прочности выполняется. 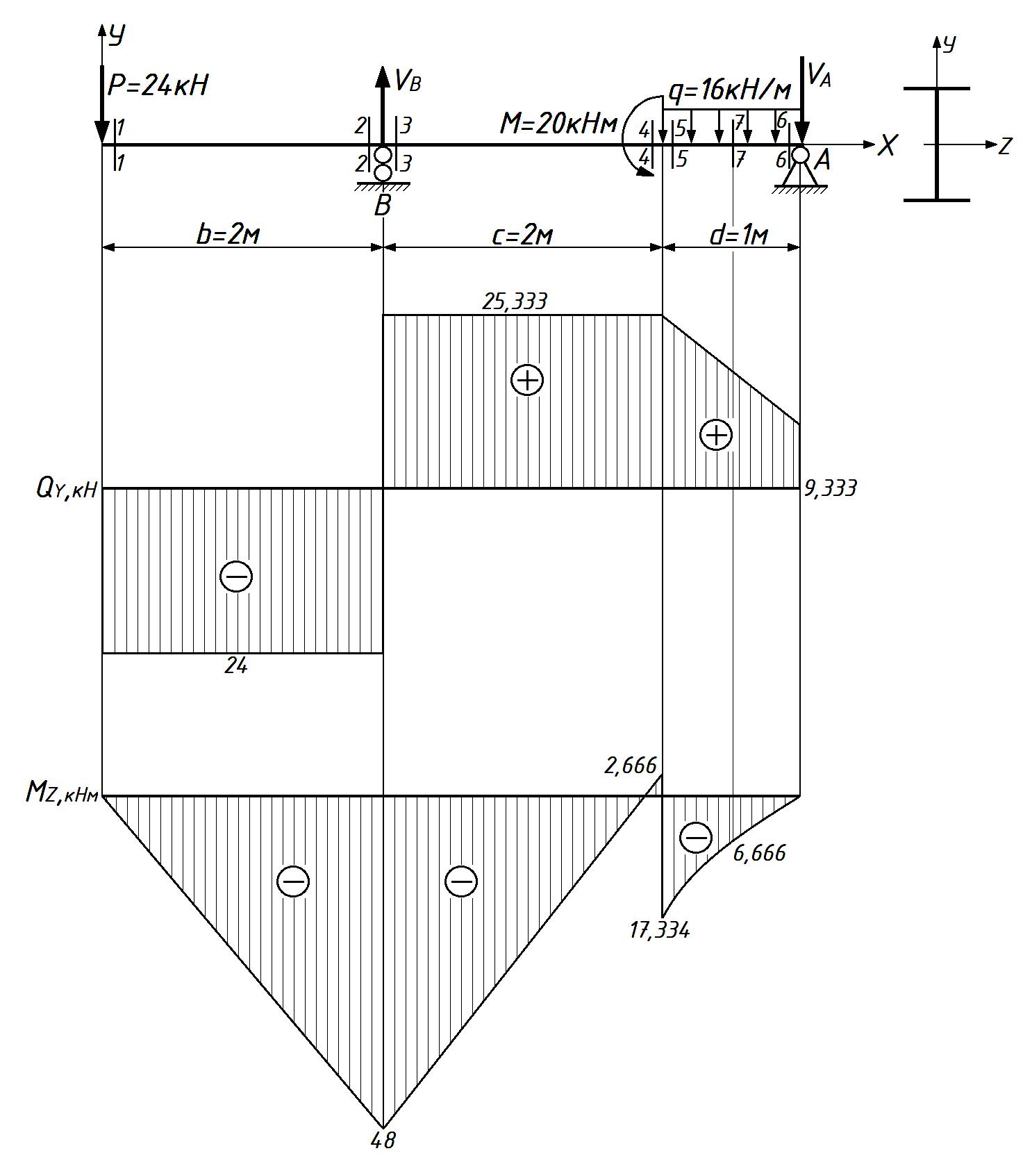 Рисунок 8. – Эпюры внутренних силовых факторов Коэффициент запаса прочности по отношению к пределу текучести, если по условию задачи 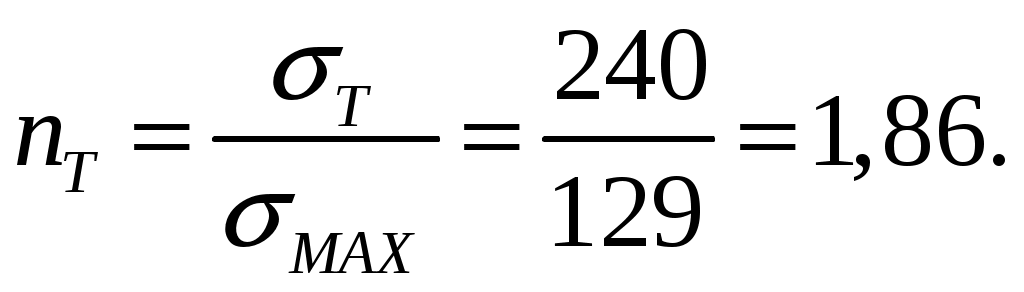 Величина ЗАДАЧА № 4 КРУЧЕНИЕ ВАЛОВ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ Для заданного вала требуется: Из условия равновесия определить направление и величину незаданного скручивающего момента. Построить эпюру крутящих моментов. Определит диаметр вала (материал – сталь Ст5) на каждом участке из условия прочности по касательным напряжениям, если Вычисленные диаметры округлить до ближайших больших целых значений. Построить эпюру углов закручивания (углов поворота) поперечных сечений вала, приняв за неподвижное левое торцовое сечение, если Данные для расчета: Решение: Вал нагружен внешними скручивающими моментами, лежащими в плоскостях, перпендикулярных продольной оси вала. 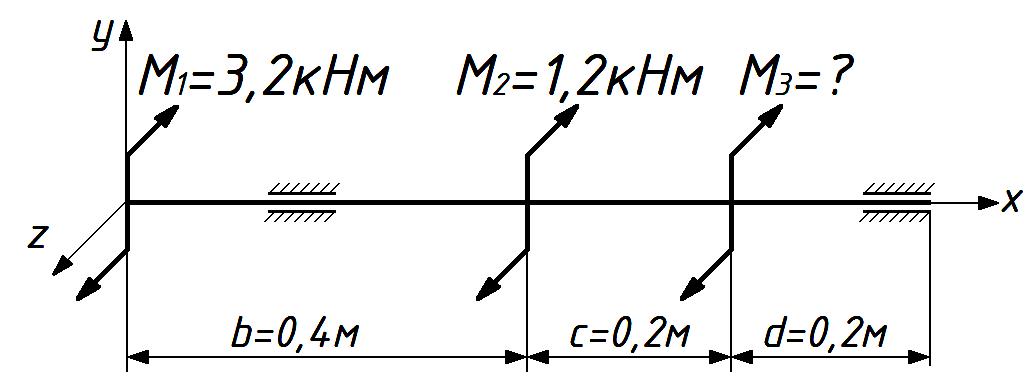 Рисунок 9. – Схема вала Зададимся системой координат, в которой ось Х – продольна ось вала. Составим уравнение равновесия относительно оси Х и найдем направление и величину неизвестного скручивающего момента М3: Знаки моментов одинаковы, так как направлены в одну сторону Знак (-) указывает на то, что действенное направление момента М3 противоположно ранее принятому Вал имеет три участка, которые различаются характером нагружения. Проведем в начале и в конце каждого участка характерные сечения и определим крутящие моменты в каждом сечении По полученным значениям строим эпюру крутящих моментов. Из условия прочности по касательным напряжениям при кручении находим диаметр на каждом участке 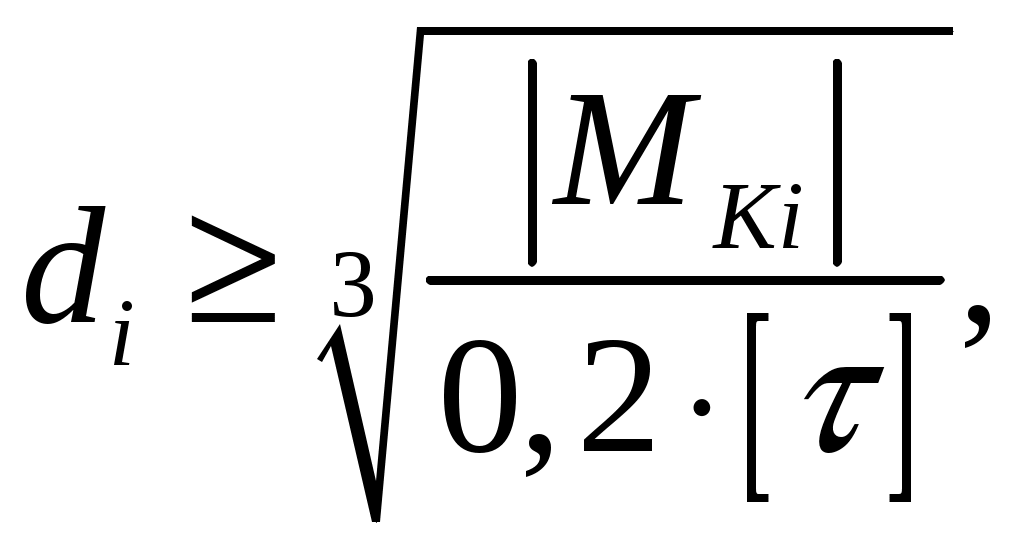 где Диаметр вала на 1 участке;  Принимаем Диаметр вала на 2 участке; 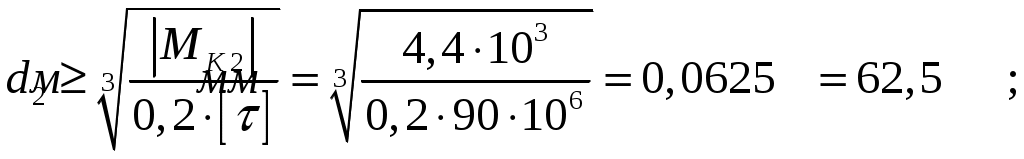 Принимаем Диаметр третьего участка равен нулю. В этом случае принимаем диаметр равный наименьшему из принятых диаметр для других участков. Принимаем Определяем углы закручивания на участках вала: 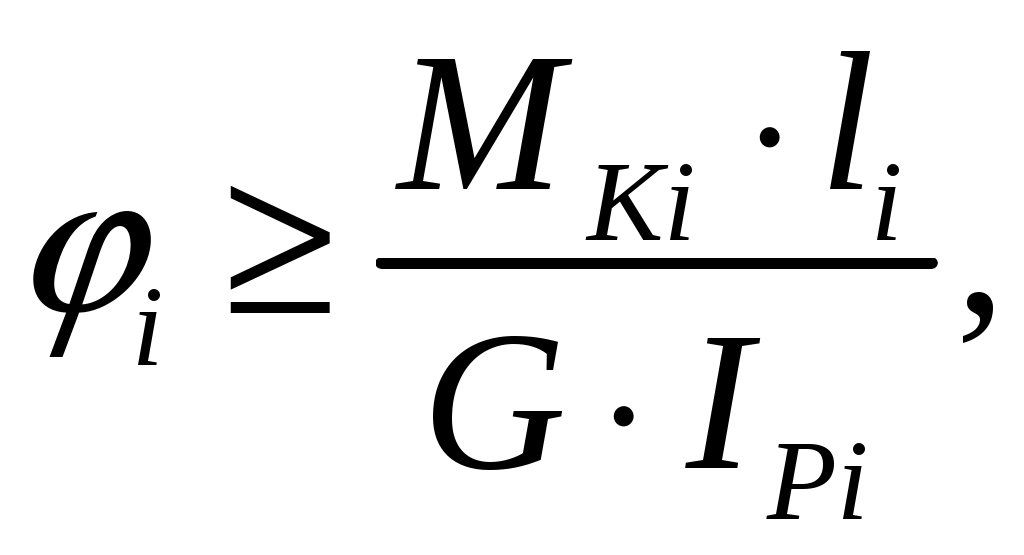 где По эпюре крутящих моментов Вычислим полярные моменты инерции сечения вала на различных участках. Определим углы закручивания участков вала: 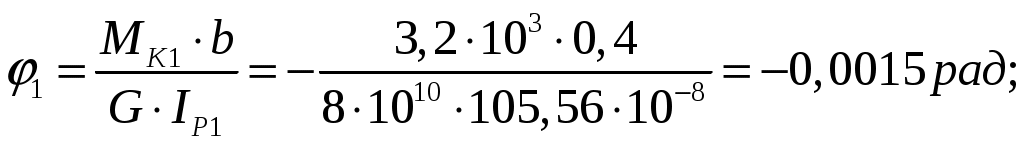 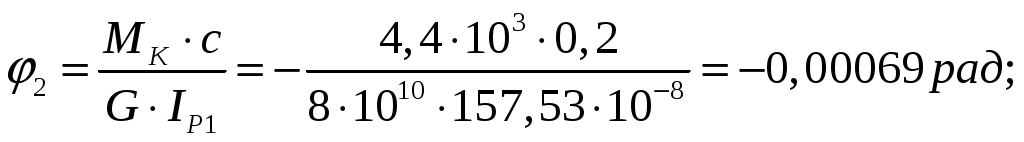 Сечения вала, совпадающие с границами участков, обозначим I, II, III, IV. Для построения эпюры углов закручивания найдем углы поворота этих участков. Будем считать левое торцовое сечение вала неподвижным, то есть По данным значениям строим эпюру углов закручивания. 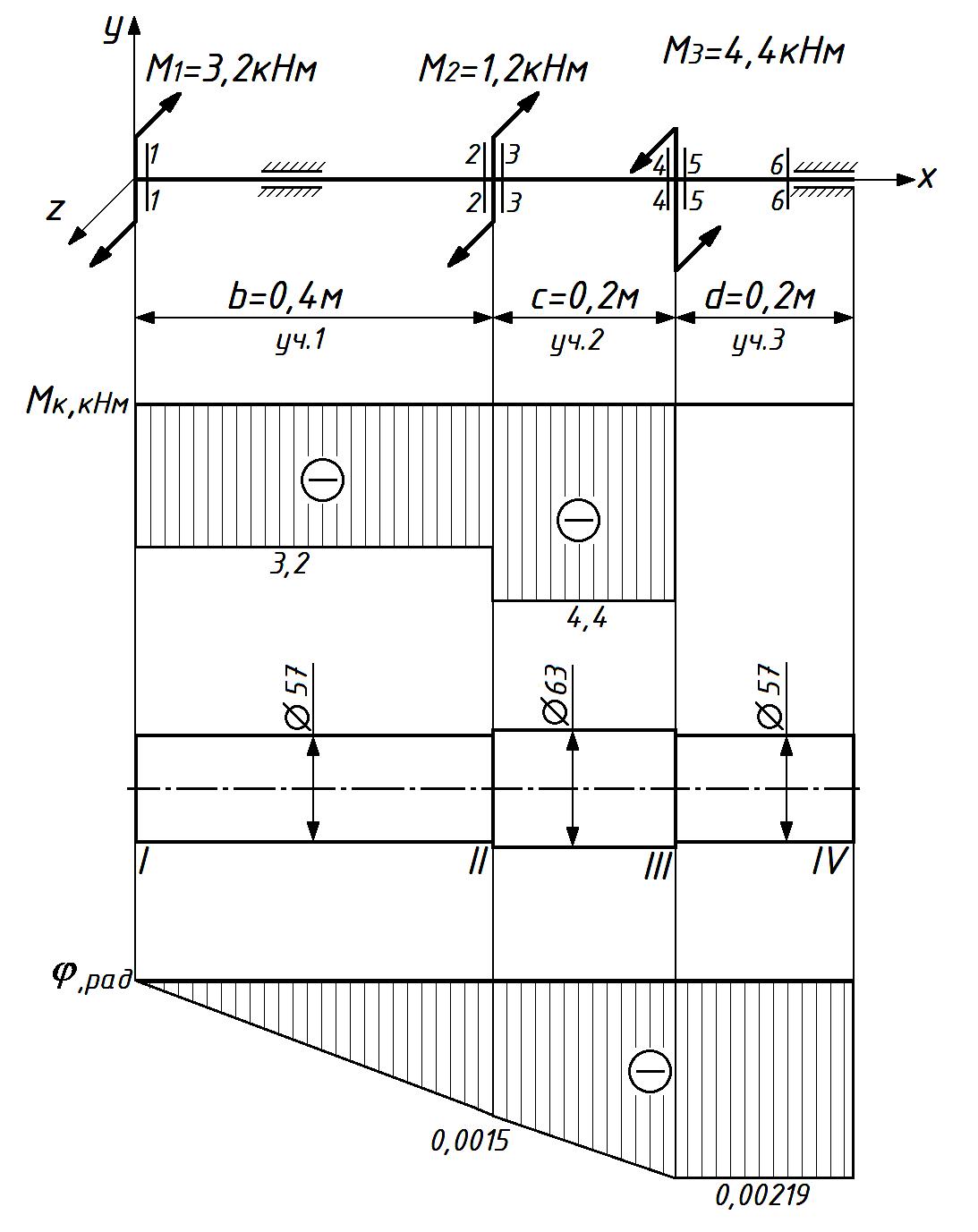 Рисунок 10 – Расчетная схема вала и эпюры крутящих моментов и углов закручивания Список использованной литературы Дарков, А.В. Сопротивление материалов. – М. : Высшая школа, 2007. – 623 с. Миролюбов И.Н. и др. Пособие по решению задач по сопротивлению материалов : учебное пособие для технических вузов. – М. : Высшая школа, 2007. – 399 с. Степин П.А. Сопротивление материалов. – М. : Высшая школа, 2008. – 303 с. Феодосьев В.И. Сопротивление материалов: Учебник для студентов высш.техн.учеб.зав. – 10-ое изд., перераб. и доп. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. – 588 с. Александров, А.В. Сопротивление материалов: учеб. Для вузов / А.В. Александров, В.Д. Потапов, Державин Б.П. – 4-ое изд. - М.: Высшая школа 2009– 560с. |
