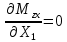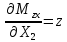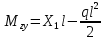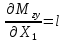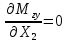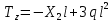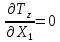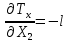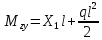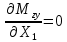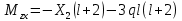сопромат. Курсовой проект по сопромату (2). Расчет статически неопределимой пространственной рамы
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
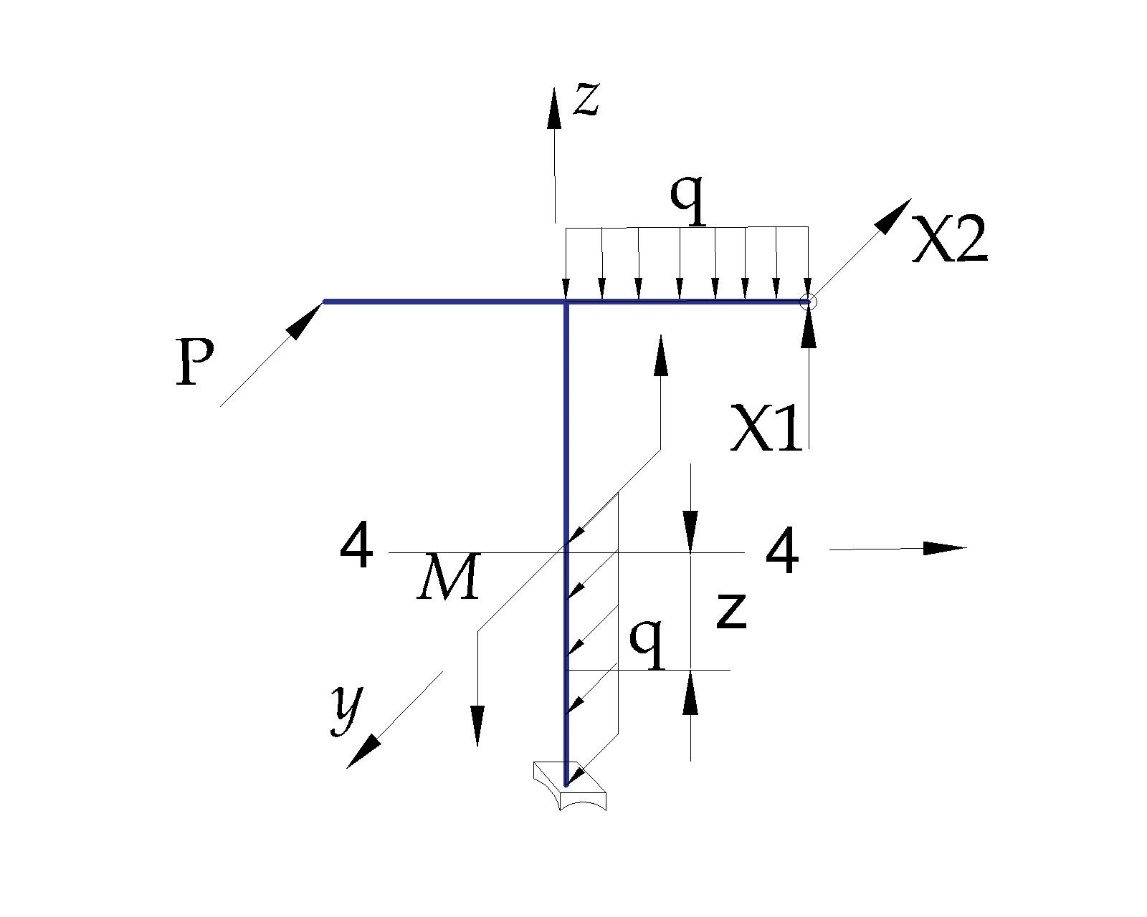
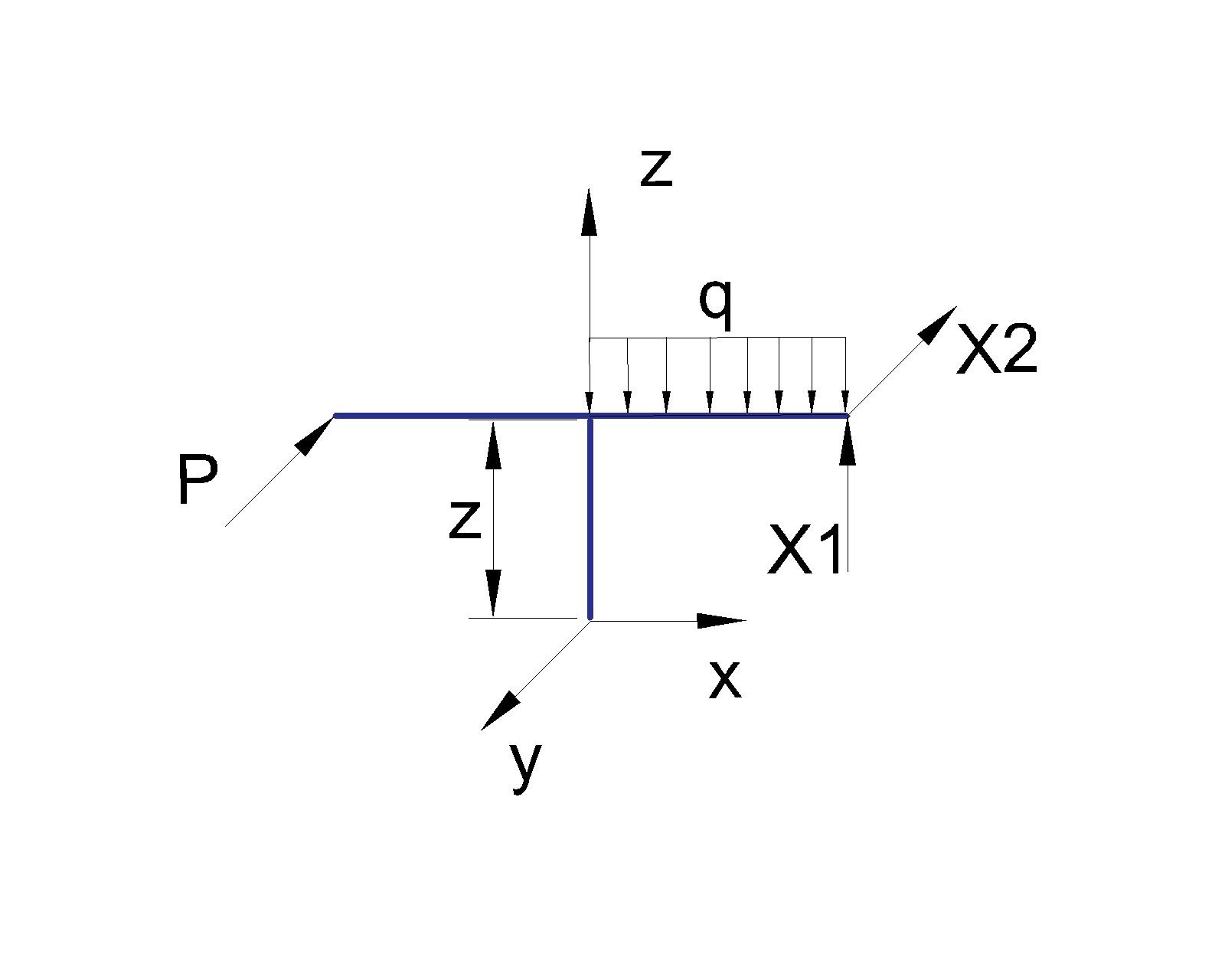
 «ТОМСКЫЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНОЙ УНИВЕРСИТЕТ» (ТГАСУ) Кафедра Строительной механики КУРСОВАЯ РАБОТА по дисциплине «Сопротивление материалов» на тему: Расчет статически неопределимой пространственной рамы. Выполнил: Студент 2 курса, гр. 0010/2 Мухторов А.Д. Проверил: Преподаватель Трепутнева П.А. Томск 2022 г. Оглавление1. Заданная система. 3 2.Решение. 3 Степень статической неопределимости пространственной рамы. 3 3. Выбор основной системы. 4 4. Выбор эквивалентной системы. 4 5. Составление системы канонических уравнений метода сил. 4 6. Вычисление коэффициентов канонических уравнений при помощи правила Верещагина. 5 7. Выполнение проверки правильности полученной системы канонических уравнений при помощи теоремы о минимуме потенциальной энергии. 7 9. Определение геометрических размеров поперечного сечения элементов рамы. Error: Reference source not found5 10. Аналитическое исследование напряженного состояния материала в двух точках опасного поперечного сечения. Error: Reference source not found6 11. Выполнение графической проверки величины главных напряжений в указанных точках опасного поперечного сечения при помощи круговых диаграмм Мора Error: Reference source not found1 12. Определение относительной деформации по направлению главных осей в указанных точках. Error: Reference source not found2 13. Построение эпюр поперечных и продольных сил…………………………………23 14. Список литературы…………………………………………………………………...24 1. Заданная система.К расчету следует принять. Внешняя нагрузка: 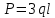 , , 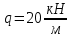 , , 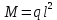 , , 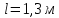 . . 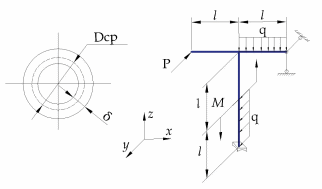  Рисунок 1. Заданная система Параметры поперечного сечения стержней рамы: 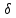 , , 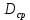 ; ; 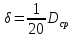 . . Механические характеристики материала для изготовления стержней: Ст.3, 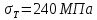 , , 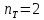 , , 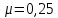 . .Решение.Степень статической неопределимости пространственной рамы.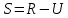 , где: , где: 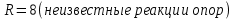 ; ; 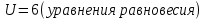 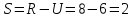 Вывод: заданная система дважды статически неопределима, так как неизвестных реакций опор восемь, а уравнений равновесия для произвольной пространственной системы сил только шесть. Она содержит две «лишние» связи. 3. Выбор основной системы.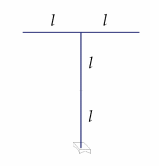  Рисунок 2. Основная система Для расчета берем основную систему, получаемую из заданной отбрасыванием лишних связей правой шарнирно - неподвижной опоры. Внешняя нагрузка к основной системе не прикладывается. Для раскрытия статической неопределимости заданной системы первоначально воспользуемся методом сил. Выберем основную систему. 4. Выбор эквивалентной системы.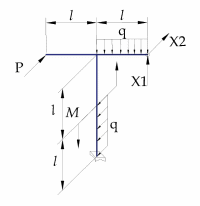  Рисунок 3. Эквивалентная система Нагружаем основную систему заданной внешней нагрузкой и неизвестными силами 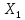 и и 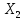 , возникающими в «лишних связях». Это и будет эквивалентная система. , возникающими в «лишних связях». Это и будет эквивалентная система.5. Составление системы канонических уравнений метода сил.Поскольку заданная система дважды статически неопределима, составим систему из двух канонических уравнений: 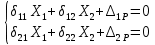 Первое и второе уравнения показывают, что суммарное линейное перемещение по направлению Х1 и по направлению Х2 равно нулю. 6. Вычисление коэффициентов канонических уравнений при помощи правила Верещагина.Для вычисления коэффициентов системы канонических уравнений, т.е. единичных и грузовых перемещений, нагружаем основную систему поочередно каждой единичной силой 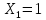 , , 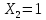 и заданной внешней нагрузкой и строим единичные и грузовые эпюры изгибающих и крутящего моментов(Рис 4,5,6,7,8). и заданной внешней нагрузкой и строим единичные и грузовые эпюры изгибающих и крутящего моментов(Рис 4,5,6,7,8). Главные единичные перемещения 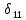 и и 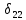 вычисляем перемножением эпюр вычисляем перемножением эпюр 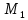 и и 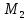 самих на себя. самих на себя.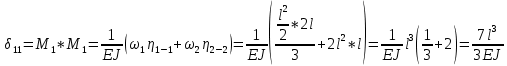 где: 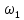 – площадь первой эпюры; – площадь первой эпюры; 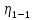 – ордината, проходящая через центр тяжести первой эпюры; – ордината, проходящая через центр тяжести первой эпюры; 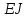 – жесткость при изгибе; – жесткость при изгибе; 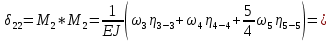 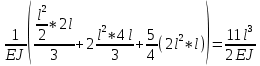 где: 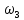 – площадь третьей эпюры; – площадь третьей эпюры; 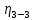 – ордината, проходящая через центр тяжести первой эпюры; – ордината, проходящая через центр тяжести первой эпюры; 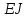 – жесткость при изгибе; – жесткость при изгибе; 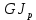 – жесткость при кручении; – жесткость при кручении; 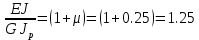 = = 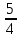 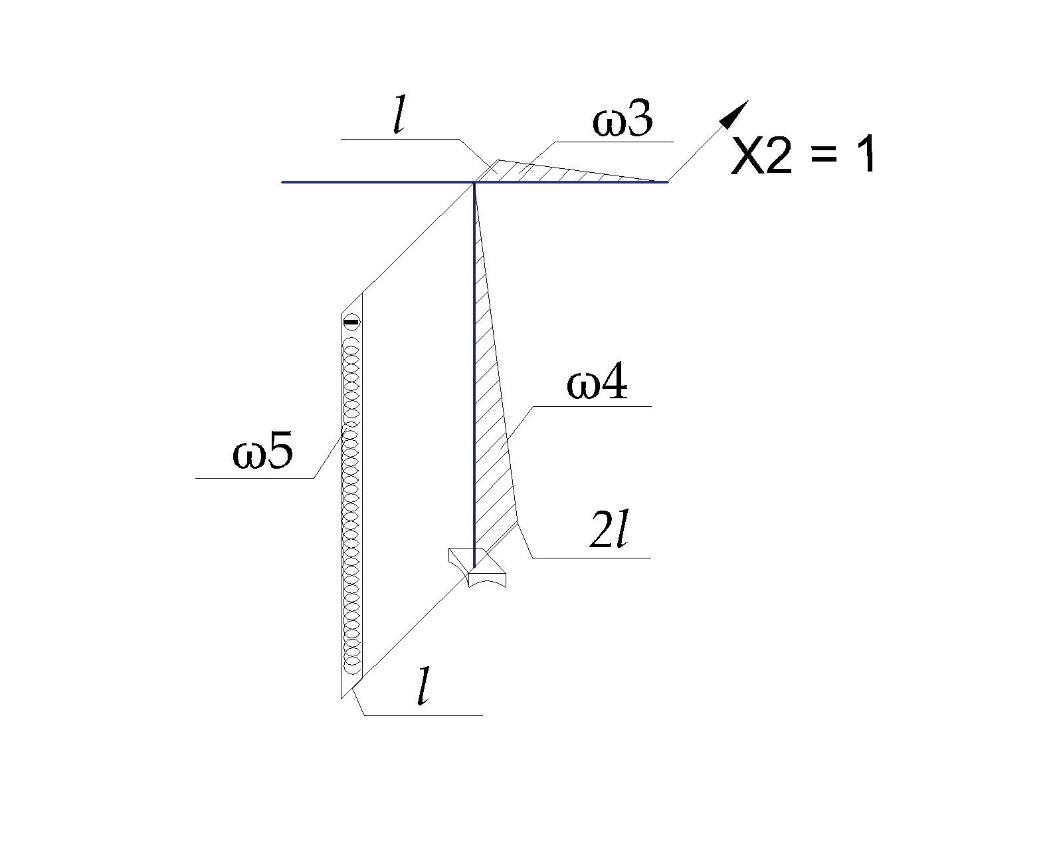 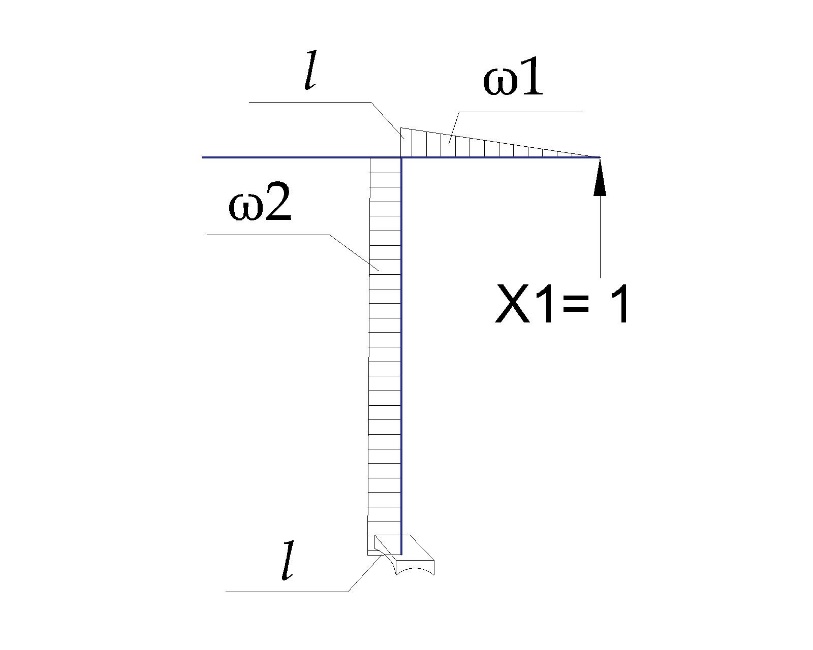   Рисунок 4. Эпюра М2 Рисунок 5. Эпюра М1 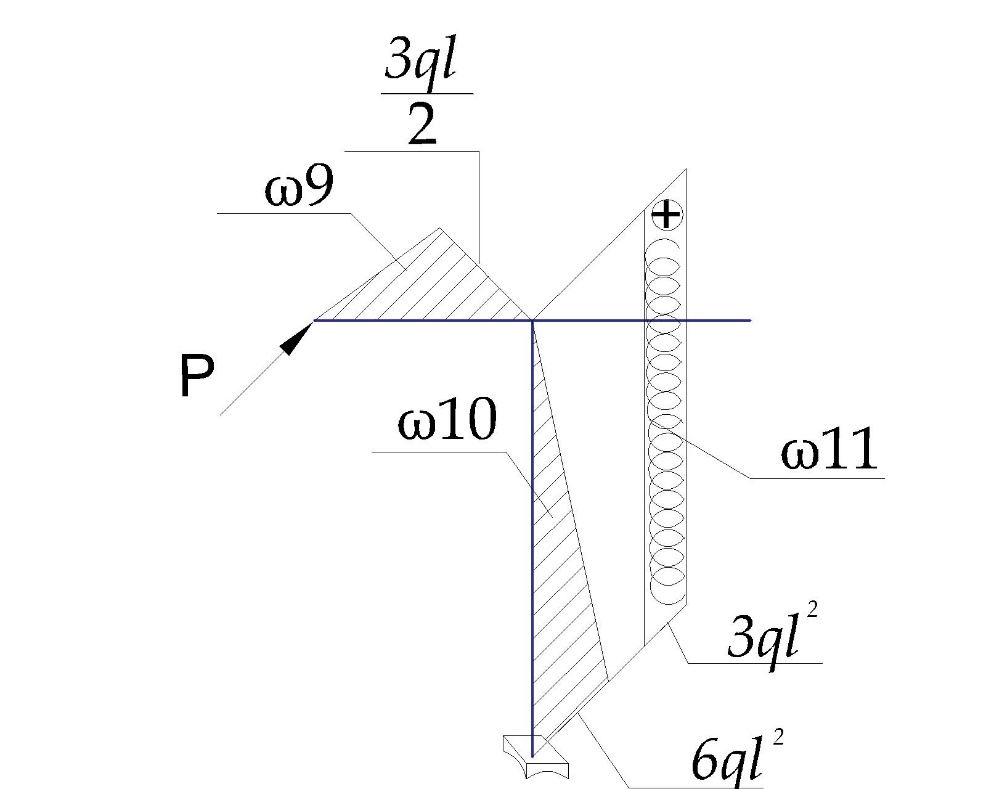  Рисунок 6. Эпюра МР  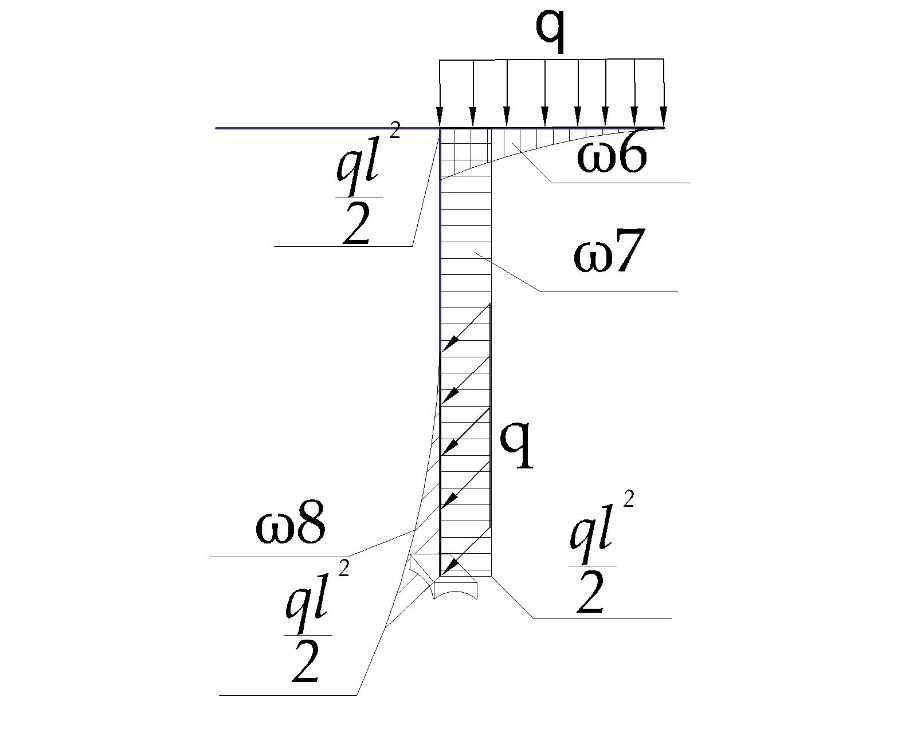 Рисунок 7. Эпюра Мq 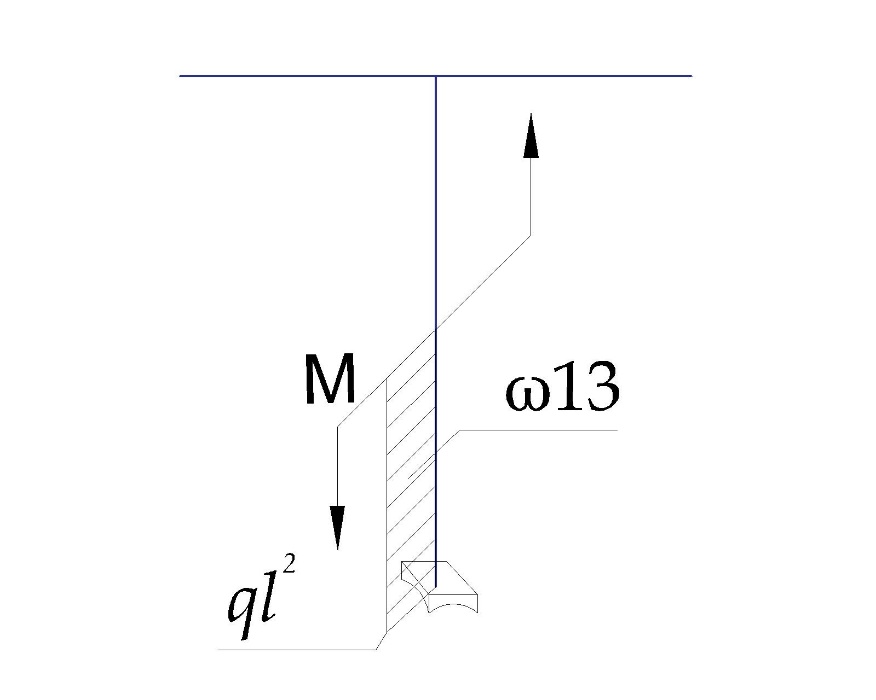  Рисунок 8. Эпюра Мm Перемножением эпюр 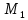 и и 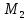 находим побочные единичные перемещения: находим побочные единичные перемещения: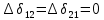 Грузовые перемещения 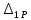 и и 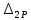 получаем путем перемножения эпюр получаем путем перемножения эпюр 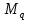 , , 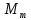 , , 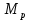 на эпюры соответственно на эпюры соответственно 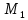 и и 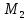 . .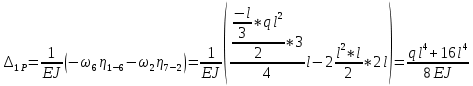 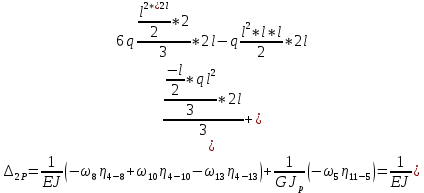 = =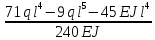 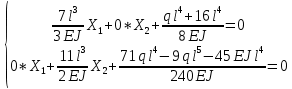 После математических преобразований будем иметь: 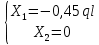 7 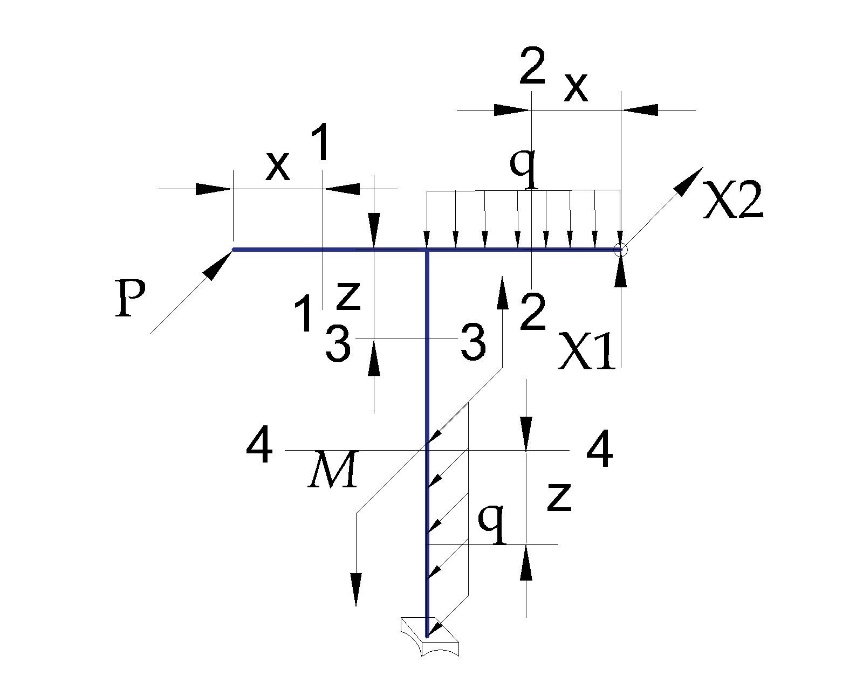 . Выполнение проверки правильности полученной системы канонических уравнений при помощи теоремы о минимуме потенциальной энергии. . Выполнение проверки правильности полученной системы канонических уравнений при помощи теоремы о минимуме потенциальной энергии. Изображаем эквивалентную систему. Записываем теорему о минимуме потенциальной энергии: 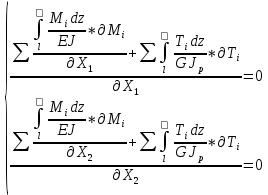  Рисунок 9. Эквивалентная система Теперь для каждого элемента рамы записываем аналитические выражения для изгибающего и крутящего моментов и определяем их частные производные по неизвестным силам 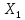 и и 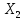 . .
Полученные результаты подставим в первое уравнение системы и проинтегрируем по всей длине каждого элементы рамы. 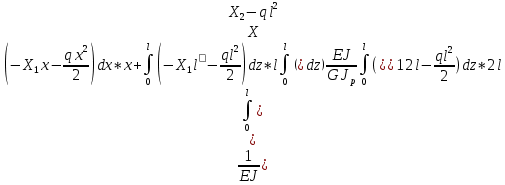 X1 = 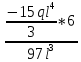 X1 = -0,45ql Далее, подставив соответствующие выражения изгибающего и крутящего моментов и их частных производных по неизвестным силам во второе уравнение системы, получим: 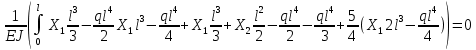 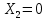 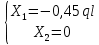 Вывод: система канонических уравнений составлена верно. 14. Список литературы 1. Феодосьев, В. И. Сопротивление материалов / В. И. Феодосьев. – М.: Наука, 1967 (1986; 1999). – 552 (512; 591) с. 2. Степин, П. А. Сопротивление материалов / П. А. Степин. – М.: Высшая школа, 1968 (1973; 1987). – 424 (328; 367) с. 3. Дарков, А. В. Сопротивление материалов / А. В. Дарков, Г. С. Шпиро. – М.: Высшая школа, 1975 (1989). – 742 (624) с. 4. Бородин, Н. А. Сопротивление материалов: учебное пособие / Н. А. Бородин. – М.: Дрофа, 2001. – 288 с. 5. Механика материалов: учебное пособие / Ю. В. Василевич [и др.]. – Минск: БНТУ, 2005. – 155 с. 6. Качурин, В. К. Сборник задач по сопротивлению материалов / В. К. Качурин. – М.: Наука, 1970. – 432 с. 7. Винокуров, Е. Ф. Справочник по сопротивлению материалов / Е. Ф. Винокуров, М. К. Балыкин, И. А. Голубев. – Минск: Наука и техника, 1988. – 464 с. | ||||||||||||||||

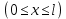
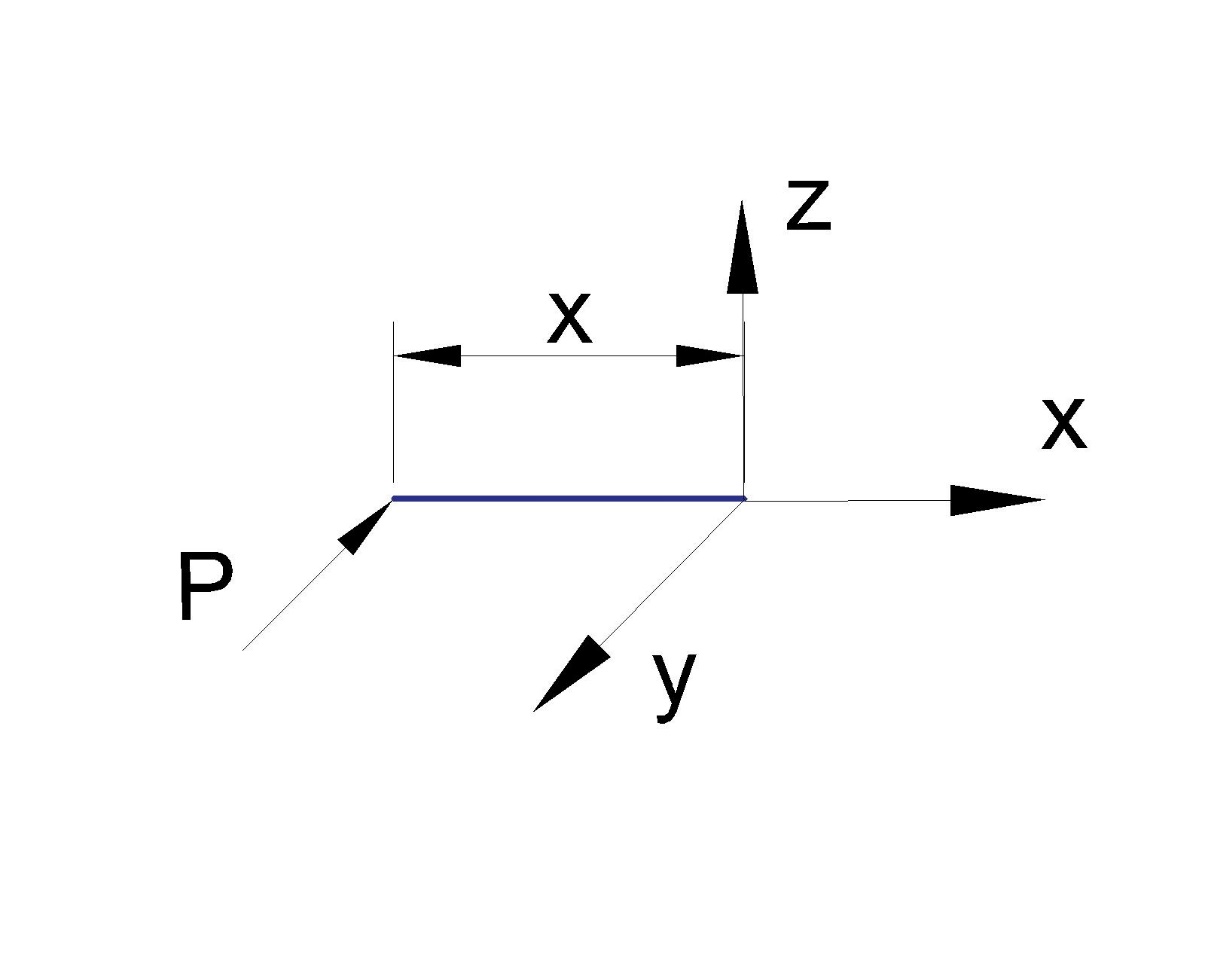
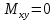
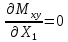
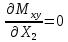
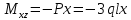
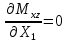
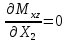
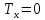
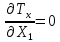
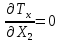
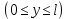
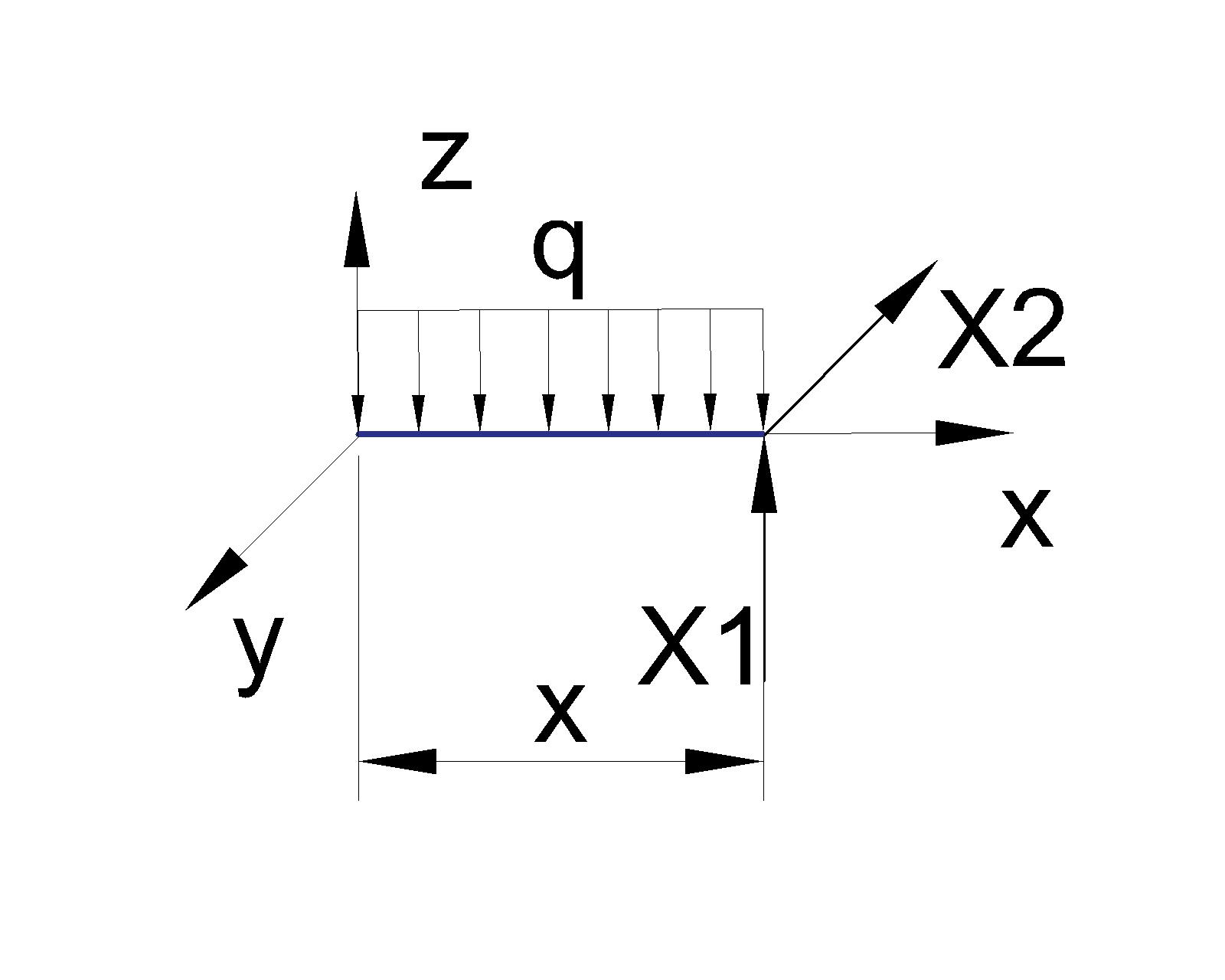
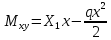
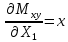
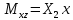
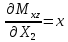
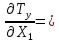 0
0 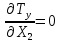
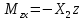 -3qlz
-3qlz