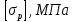Сопромат 3сем 1вар. Расчет статически неопределимой стержневой системы Условие задачи
 Скачать 66.85 Kb. Скачать 66.85 Kb.
|
|
Условие задачи Составить уравнения статики и уравнения совместности деформаций. По найденным усилиям в стержнях и заданным допускаемым напряжениям вычислить необходимые площади поперечных сечений стержней. Руководствуясь этими площадями и заданными соотношениями, подобрать окончательные размеры площадей. Определить истинный коэффициент запаса прочности в каждом стержне. Построить действительный план перемещений. Плоская статически неопределимая стержневая система нагружена в соответствии с заданной исходной схемой (рис. 1.1). Стержни изготовлены из разных материалов, нормативные коэффициенты и механические характеристики которых приведены ниже в таблице 1.1. Исходные данные Исходные данные Таблица 1.1
 Решение задачи Выбираем систему координат x, y(рис. 1.2). Рассматриваем условия равновесия твердого тела, прикладывая к нему внешнюю нагрузку P и реакции от стержней Ni(i=1, 2, 3). Так как линии действия всех сил сходятся в одной точке, то для плоской системы можем составить 2 линейно – независимых уравнения равновесия: 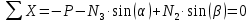 (1) (1)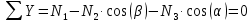 (2) (2) Имеем 3 неизвестных усилия N и 2 линейно – независимых уравнения равновесия, 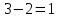 , следовательно, задача 1 раз статически неопределима. Уравнения (1) и (2) следует дополнить одним уравнением совместности деформаций. Для этого найдем удлинения всех стержней после деформации. Предположим, что под действием внешних усилий система переместилась из точки A в точку A'. Удобнее всего выразить удлинение 1 стержня через удлинения 2 и 3 стержней. , следовательно, задача 1 раз статически неопределима. Уравнения (1) и (2) следует дополнить одним уравнением совместности деформаций. Для этого найдем удлинения всех стержней после деформации. Предположим, что под действием внешних усилий система переместилась из точки A в точку A'. Удобнее всего выразить удлинение 1 стержня через удлинения 2 и 3 стержней. 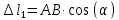 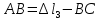 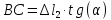 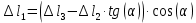 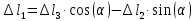 (3) (3)Уравнение (3) есть искомое уравнение совместности деформаций для рассматриваемой задачи. Далее выразим удлинения 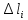 через усилия в стержнях через усилия в стержнях 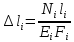 , стержень 3 сжимается, следовательно, продольная сила в нем отрицательная, учитывая этот минус, получаем: , стержень 3 сжимается, следовательно, продольная сила в нем отрицательная, учитывая этот минус, получаем: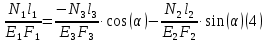 Учитывая заданное соотношение площадей (табл. 1), принимаем: 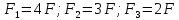 Здесь F – неизвестная площадь Аналогично следует, что: 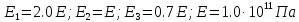 Длины стержней определяются из рис. 1: 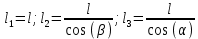 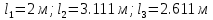 Подставляя полученные выражения в (4) и сокращая на общий множитель 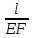 , получаем: , получаем: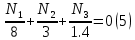 Система уравнений (1), (2), (5) позволяет определить усилия в стержнях: 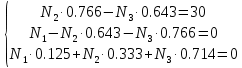 Данная система была решена в Microsoft Office Excel методом обратной матрицы. Записываем в Excel матрицу А и матрицу B. С помощью встроенной программы МОБР находим обратную матрицу, обратную А - 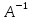 . С помощью встроенной программы МУМНОЖ находим значение столбца Х, перемножая матрицы . С помощью встроенной программы МУМНОЖ находим значение столбца Х, перемножая матрицы 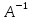 и В. и В. 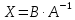 – формула нахождения корней системы. – формула нахождения корней системы.Решая систему, получаем: 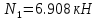 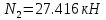 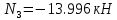 Проверка правильности решения: 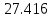 ·0.766-( ·0.766-(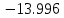 )·0.643 ≈ 30 )·0.643 ≈ 30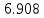 - -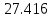 ·0.643-(- ·0.643-(-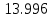 )·0.766 ≈ 0 )·0.766 ≈ 0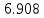 ·0.125+ ·0.125+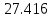 ·0.333+(- ·0.333+(-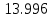 )·0.714 ≈ 0 )·0.714 ≈ 0Далее необходимо определить площади поперечных сечений стержней при расчете по допускаемым напряжениям. 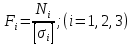 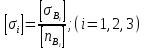 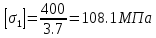 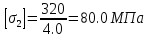 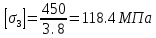 Учитывая соотношения площадей, найдем: 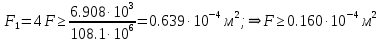 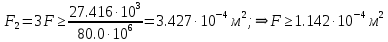 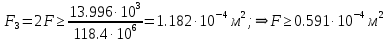 За допускаемое значение F принимаем максимальное из всех полученных 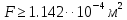 . Так как максимум реализуется для 2 стержня, то напряжение в нем будет равно допускаемому, а напряжения в других стержнях будут меньше допускаемых. . Так как максимум реализуется для 2 стержня, то напряжение в нем будет равно допускаемому, а напряжения в других стержнях будут меньше допускаемых. Найдем действительные площади стержней: 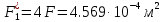 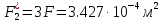 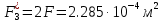 Вычислим истинные коэффициенты запаса прочности 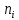 каждого стержня: каждого стержня: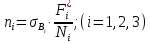 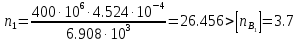 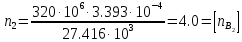 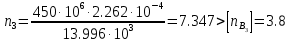 Используя найденные значения усилий, найдем удлинения стержней: 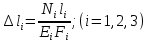 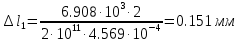 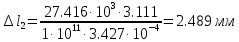 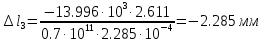 Для проверки правильности полученного решения строим действительный план перемещений (рис. 1.3). С этой целью на расчетной схеме откладываем в масштабе вычисленные перемещения 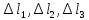 . Если вычисления были выполнены правильно, то восстановленные перпендикуляры к точкам 1, 2, 3 должны пройти через точку A'. . Если вычисления были выполнены правильно, то восстановленные перпендикуляры к точкам 1, 2, 3 должны пройти через точку A'.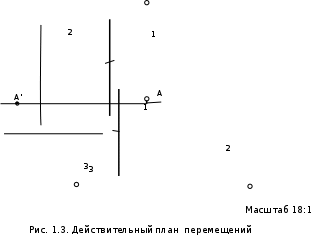 Вывод В результате решения задачи были найдены усилия в стержнях 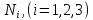 , рассчитаны площади поперечных сечений стержней, был построен план действительных перемещений стержней, все проверки сошлись, что может свидетельствовать о правильности полученных результатов. , рассчитаны площади поперечных сечений стержней, был построен план действительных перемещений стержней, все проверки сошлись, что может свидетельствовать о правильности полученных результатов. Определение допускаемой нагрузки из условия прочности балки Условие задачи Чугунная балка нагружена в соответствии с расчетной схемой. Требуется вычислить геометрические характеристики заданного сечения и определить допускаемую нагрузку 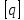 из условия прочности и рационального расположения сечения. Ниже приведены исходные данные (табл. 2.1) из условия прочности и рационального расположения сечения. Ниже приведены исходные данные (табл. 2.1)Исходные данные Исходные данные Таблица 2.1
Пусть задана расчетная схема (рис. 2.1) и построены эпюры (рис. 2.2). Заданная схема поперечного сечения балки показана на рис. 2.3. 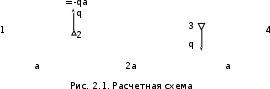 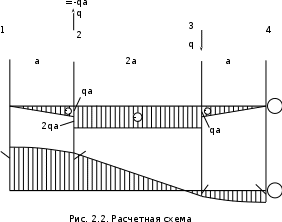  Решение задачи Разбиваем сечение на простейшие фигуры, для которых известно положение центров сечений. В данном случае это 2 прямоугольника. В данном случае удобно воспользоваться приемом «отрицательных» площадей. Полагаем, что внешний прямоугольник имеет положительную площадь, а внутренний квадрат – отрицательную. Координата центра тяжести сечения (точка C на рис. 2.4) вычисляется по формуле: 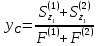 Ось  можно совместить с центром тяжести прямоугольника. При этом можно совместить с центром тяжести прямоугольника. При этом  . .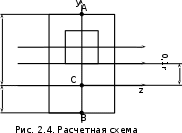 Площади и статические моменты отдельных фигур есть: 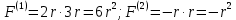 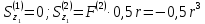 Таким образом, координата центра тяжести определится как: 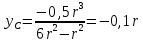 Координаты наиболее удаленных точек от оси zбудут равны: 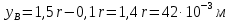 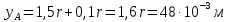 Момент инерции всего сечения относительно оси z: 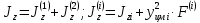 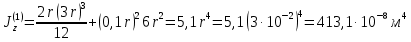 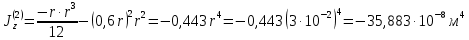 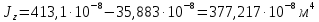 Момент инерции 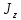 является главным центральным моментом инерции поперечного сечения балки, изображенного на рис. 2.3. является главным центральным моментом инерции поперечного сечения балки, изображенного на рис. 2.3.Наибольший изгибающий момент равен 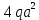 . Так как значение момента положительно, то верхние волокна сечения сжаты, а нижние растянуты. В связи с тем, что материал балки лучше работает на сжатие . Так как значение момента положительно, то верхние волокна сечения сжаты, а нижние растянуты. В связи с тем, что материал балки лучше работает на сжатие 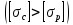 , рациональным расположением сечения будет такое, при котором наиболее удаленные от главной оси волокна (точка A на рис. 2.4) оказываются в сжатой зоне. Так же необходимо проверить сечение с максимальным значением изгибающего момента противоположного знака, это значение равно , рациональным расположением сечения будет такое, при котором наиболее удаленные от главной оси волокна (точка A на рис. 2.4) оказываются в сжатой зоне. Так же необходимо проверить сечение с максимальным значением изгибающего момента противоположного знака, это значение равно 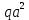 . .В растянутой зоне: 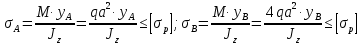 В сжатой зоне: 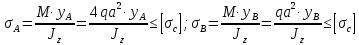 Подставляя числовые значения, определим допускаемую нагрузку: 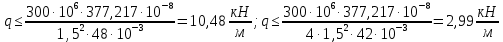 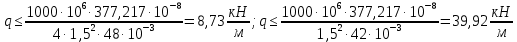 За нагрузку принимаем наименьшее значение 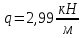 , которая была получена из расчета на растяжение. , которая была получена из расчета на растяжение.На рис. 2.5 показано рациональное расположение сечения. 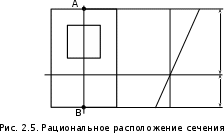 Вывод В ходе выполнения задачи были вычислены геометрические характеристики балки, рассчитана допускаемая нагрузка 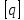 , было определено рациональное расположение сечения балки. , было определено рациональное расположение сечения балки. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||

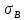
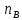 ]
]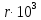 , м
, м