БДР18. Проектирование двускатной решетчатой балки бдр18
 Скачать 7.36 Mb. Скачать 7.36 Mb.
|
|
Проектирование двускатной решетчатой балки БДР18 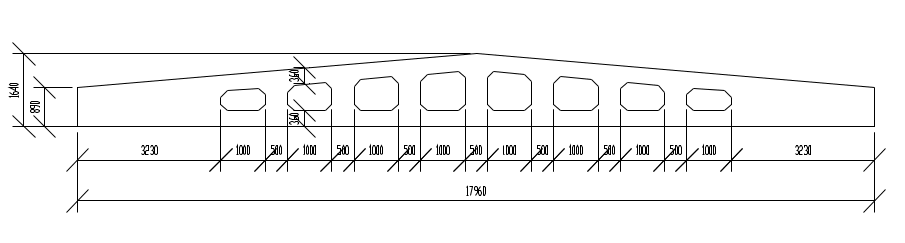 Для анализа напряженного состояния элементов решетчатой балки при помощи программного комплекса SCAD был проведен расчет усилий, возникающих в элементах конструкции балки от суммарного действия постоянной и снеговой нагрузки, как показано на рисунке 1, 2, 3 и построены эпюры усилий N, M, Q. Согласно эпюрам N, M, Q по наиболее неблагоприятным сочетаниям усилий проведем расчет прочности нормальных и наклонных сечений верхнего и нижнего поясов балки, а также ее стоек. 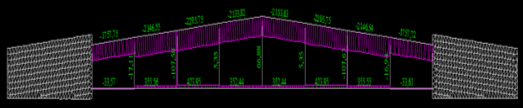 Рис. 1. Схема эпюр N (кН) в элементах балки 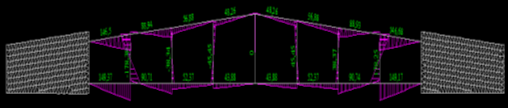 Рис. 2. Схема эпюр М (кНм) в элементах балки  Рис. 3. Схема эпюр Q (кН) в элементах балки Расчет нижнего ПН пояса: подбор арматуры. В нижнем поясе балки принимается несимметричное армирование. 1. Расчетные усилия в сечении нижнего пояса: N=423,95 кН, M=52,37кНм. Принимаем размеры поперечного сечения b=0,20 м; h=0,36м; - величина защитного слоя бетона as=as' = 0,05м. 2. По приложению 3 для указанного в задании класса ПН арматуры А600 определяем Rs=520 МПа, Es = 200 000МПа. 3. Рабочая высота сечения h0 = h-aS=0,36− 0,05 = 0,31м . 4. Эксцентриситет продольного усилия относительно центра тяжести сечения нижнего пояса: e0= 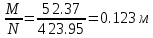 . .5.Эксцентриситет продольного усилия относительно граней сечения соответственно верхней и нижней: 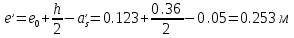 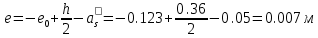 6. Kоэффициент η =1,1. 7. Площадь растянутой и менее растянутой арматуры в сечении нижнего пояса: 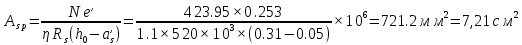 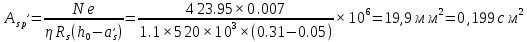 8. Принимаем нижнюю арматуру 2 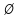 22А600 Asp =7,6 см2 , dsp = 22мм , а верхнюю 2 22А600 Asp =7,6 см2 , dsp = 22мм , а верхнюю 2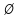 4Вр500 As′p = 0,25см2 , ds′p = 4мм. 4Вр500 As′p = 0,25см2 , ds′p = 4мм.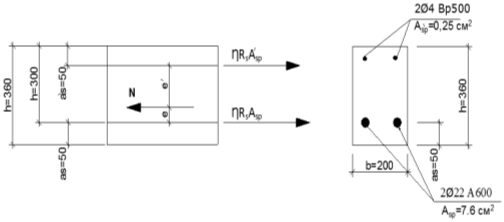 Рис. 4. К подбору продольной арматуры в нижнем растянутом поясе Расчет нижнего предварительно напрягаемого пояса образование трещин. 1. Дополнительные данные необходимые для расчета: - класс бетона В30; - условия твердения – подвергнутый тепловлажностной обработке; - способ натяжения арматуры – механический; - средний коэффициент надежности по нагрузке γfm=1,16 ; - длина растянутого пояса L =18,0м. 2. Нормативная прочность бетона при растяжении Rbt,ser=1.75МПа, модуль упругости бетона Eb=32,5 ·103 МПа, нормативная прочность арматуры: А600 - Rs,ser =600МПа, модуль упругости арматуры Es=2·105 МПа Вр 500 - Rs,ser =500МПа , модуль упругости арматуры Es=1,7·105 МПа 3. Назначаем величину предварительных напряжений: σsp = 0,9⋅ Rs,ser =0,9⋅ 600 = 540МПа . 4. Величина предварительного напряжения: σsp = σs′p = 0,9⋅540 = 486МПа . 5. Потери от релаксации арматуры Δσsp1 = 0,1·486 – 20=28,6МПа. 6. Потери от перепада температуры при тепловлажностной обработки бетона: Δσsp2 =1,25·65=81,25МПа. 7. Потери от деформации стальной формы Δσsp3 =30МПа. 8. Потери от деформации анкеров Δσsp4 = 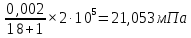 9. Первые суммарные потери в ПН арматуре: σlos,1 =28,6+81,25+30+21,053=160,903мПа. 10. Деформация усадки бетона εb,sh=25·10-5. 11. Потери от усадки бетона Δσsp5 = 25·10-5 ·2·105 =50 МПа. 12. Коэффициент ползучести при влажности воздуха 65% φb,сr=1,9 13. Коэффициент приведения арматуры к бетону: α = Es/Eb=2·105 /32,5 ·103=6,154 - А600 α/ = Es/Eb=1,7·105 /32,5 ·103=5,230 – Вр500 14. Коэффициент армирования сечения: 6 µsp= 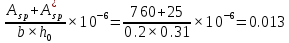 15. Усилие предварительного обжатия с учетом первых потерь: P(1) = ( 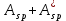 ) )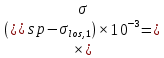 (760+25)·(486 -160,903) ·10-3=255,2кН. (760+25)·(486 -160,903) ·10-3=255,2кН.16. Приведенная площадь сечения: Ared = 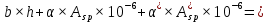 0,2·0,36+6.154·760·10-6+5.23·25·10-6=0,076м2. 0,2·0,36+6.154·760·10-6+5.23·25·10-6=0,076м2.17. Приведенный статический момент: 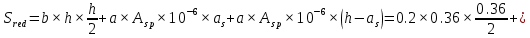 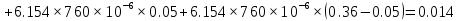 18. Центр тяжести приведенного сечения относительно наиболее растянутой грани решетчатый балка напряжение арматура 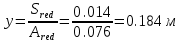 19. Момент инерции бетонного сечения: 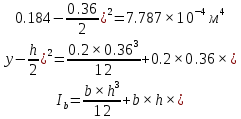 20. Момент инерции нижней и верхней арматуры: 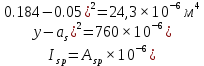 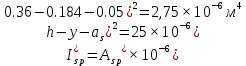 21. Приведенный момент инерции сечения нижнего пояса балки: Ired =Ib×10-4 +a×Isp×10-6 +a×Isp/ ×10-6 =7.787×10-4 + 6.154×24,3×10-6 +6.154×2,75 ×10-6 =9,45×10-4 м4 22. Расстояние от ц.т. приведенного сечения до ц.т. арматуры соответственно нижней и верхней: ysp=y-as =0.184-0.05=0.134 м. ysp/=h-y-as =0,36-0.184-0.05=0,126 м. 23. Эксцентриситет усилия обжатия с учетом первых потерь: e0p1= 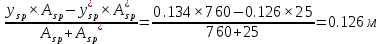 24. Напряжения в бетоне на уровне ц.т. нижней и верхней арматуры: 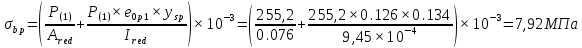 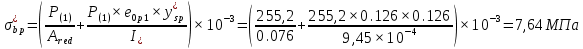 25. Потери от ползучести бетона: 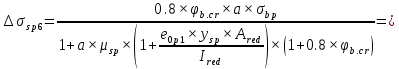 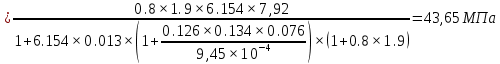 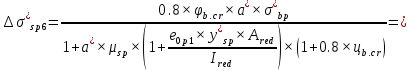 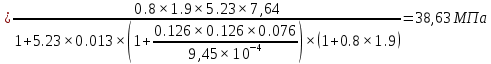 26. Так как σbp > 0 , т.е. потери от ползучести следует учитывать. 26 б. Вторые суммарные потери в верхней и нижней арматуре: 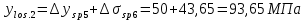 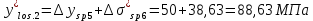 27. Значение полных потерь: 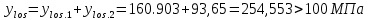  28. ПН с учетом всех потерь:   29. Коэффициент учета пластичности γ =1,3 30. Упругий момент сопротивления приведенного сечения:  31. Ядровое расстояние  32. Усилие обжатия с учетом всех потерь: P =  кН. кН.33. Эксцентриситет усилия обжатия с учетом всех потерь:  34. Момент трещиностойкости: Mcrc =  кНм кНм35. Нормативное усилие от постоянной и полной снеговой нагрузки: Ntot =  кН кН36. Эксцентриситет продольного усилия относительно ц.т. сечения: e0=0,123м. 37. Момент усилия Ntot относительно ядровой точки:  38. Так как действующий момент Mr >Mcrc, то трещины образуются и необходимо проверить их ширину раскрытия. Расчет нижнего ПН пояса на раскрытие трещин. 1. Усилие в нижнем поясе балки от постоянной нагрузки Ng=30,97кН, Mg=2,26кН. 2. Продольная сила от продолжительного действия длительных нагрузок:  3. Значение продольной силы в момент образования трещины:  4. Расстояние от ц.т. приведенного сечения до точки приложения продольной силы:  м. м.5. Расстояние от ц.т. приведенного сечения до точки приложения усилия обжатия Р:  м м6. Плечо внутренней пары сил z = b-as =0,2 − 0,05 = 0,15м . 7.1. Напряжения в растянутой арматуре от усилия Ntot :  7.2. Напряжения в растянутой арматуре от усилия Nl :  7.3. Напряжения в растянутой арматуре от усилия Ncrc :  8. Так как 394,56 МПа < 520 МПа, прочность нижней арматуры на разрыв обеспечена. 9. Поправочный коэффициент, учитывающий пластичность k = 0,9. 10. Высота растянутой зоны как для упругого материала:  11. Высота растянутой зоны с учетом пластичности:  12-13. Высота растянутой зоны сечения должна удовлетворять требованиям: yt ≥2×0.5=0.1м. y t ≤0,5×0,36= 0.18м Исходя из условий принимаем yt =0,1 м. Тогда площадь сечения растянутого бетона равна: Abt = b×yt =0,2×0,1 = 0,02 м2 . 14. Базовое расстояние между трещинами:  что больше чем 10ds =220мм. 15.1. Коэффициент совместной работы бетона и арматуры при полной нагрузке (но не менее 0,2): 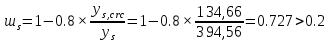 15.2. Коэффициент совместной работы бетона и арматуры при постоянной и временной длительной нагрузке: 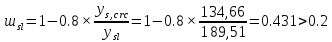 16. определяем опытные коэффициенты: 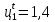 – коэф. учитывающий продолжительность действия нагрузки, – коэф. учитывающий продолжительность действия нагрузки,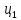 =1 - коэф. учитывающий характер нагружения для изгибаемых элементов =1 - коэф. учитывающий характер нагружения для изгибаемых элементов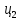 =0,5 – коэф. Учитывающий профиль продольной арматуры =0,5 – коэф. Учитывающий профиль продольной арматуры17.1. Ширина раскрытия трещин от длительного действия постоянных и временных длительных нагрузок равна: 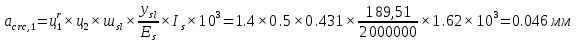 17.2. Ширина раскрытия трещин от кратковременного действия полной нагрузки: 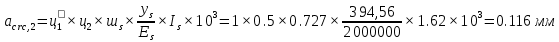 17.3. Ширина раскрытия трещин от кратковременного действия постоянных и временных длительных нагрузок: 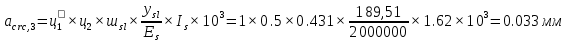 18а. Продолжительная ширина раскрытия трещин aτcrc=acrc,1=0.046 мм. 18б. Непродолжительная ширина раскрытия трещин: acrc = acrc,1 + acrc,2 + acrc,3 =0.046+0.116+0.033=0.195мм 20. Так как расчетные значение ширины раскрытия трещин acrc =0,195 не более предельных допускаемых значений, то трещиностойкость нижнего пояса обеспечена. Расчет нижнего ПН пояса на прочность по сечениям, наклонным к продольной оси. 1. По результатам статического расчета балки получено значение максимальной поперечной силы на опоре Qmax= -100.9 кН и сопутствующего значения продольной силы N =-33.57 кН. Класс конструктивной поперечной арматуры В500. 2. Влияния длительной нагрузки на прочность бетона учитывается коэффициентом γb1 = 0,9 . 3. Прочностные характеристики бетона и арматуры: при сжатии Rb=17,0 МПа, при растяжении Rbt=1,15 МПа, расчетное сопротивление хомутов растяжению Rsw= 300 МПа. 4. Прочность бетона с учетом длительности действия нагрузки: Rb= 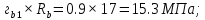 Rbt = 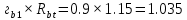 МПа. МПа.5. Коэффициент, учитывающий влияние растяжения нижнего пояса: 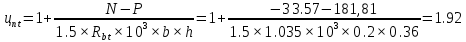 6. Изгибающий момент в наклонном сечении, воспринимаемый бетоном: 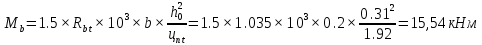 7. Так как значение поперечной силы по длине панели постоянна, длина проекции наклонного сечения c = 3×b =3×0.2=0.6 м < l1 =0,7м. Поэтому принимаем с = 0,6 м. 8. Поперечная сила, воспринимаемая бетоном: Qb =  =25,9кН =25,9кН9. Так как Qmax =100.9 кН > Qb=25,9 кН, поперечная арматура в нижнем поясе требуется. 10. Конструктивный шаг поперечных стержней (принимаем кратным 50мм):  Принимаем шаг sw = 100 мм (значение кратное 50 мм). 11. Конструктивный диаметр поперечных стержней dsw = 4мм из проволоки класса В500 12. Интенсивность поперечных стержней:  13. Так как Qb =25,9 кН < 2,5·1,035·103·0,2·0,31 = 160,42кН, то значение Qb не корректируем. 14. Определяем значение длины проекции наклонной трещины:  15. Поскольку с0 =0,45м < 2·0,31=0,62м, его значение не корректируем. 16. Несущая способность поперечных стержней в наклонном сечении: 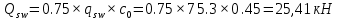 17. Так как Qmax =100,9 кН >Qb + 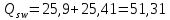 кН ,следовательно, при расчете верхнего пояса на действие поперечной силы принимаем ΔQ = +49,59 кН. кН ,следовательно, при расчете верхнего пояса на действие поперечной силы принимаем ΔQ = +49,59 кН.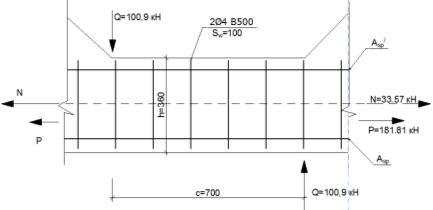 Рис. 5. К расчету сечений нижнего пояса балки Расчет верхнего пояса: подбор арматуры. 1. По результатам статического расчета определены усилия в верхнем поясе балки (рис. 1 и 2): N=2205.75 кН, M=56.88 кНм. Размеры поперечного сечения b=0,2м; h=0,36м; величина защитного слоя бетона as = a's= 0,04 м. Длина панели верхнего пояса l = 1,5 м. 2. Коэффициент влияния длительности нагрузки γb1 =0,9. 3. Для ненапрягаемой арматуры стропильной конструкции класс А400 расчетные сопротивления Rs= Rsс = 355 МПа. 4. Расчетные сопротивления бетона сжатию с учетом коэффициента условия работы: 0,9 Rb=0,9·17=15.3 МПа. 5. Величина случайного эксцентриситета: 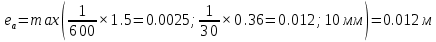 6. Так как e0=M/N=56.18/ 2205.75 =0,025м < 0,36/8 = 0,045м, расчетная длина панели верхнего пояса: l0=0.9×1.5=1.35 м 7. При классе бетона В30 и е0>ea 8. Поскольку 0.025/0,36=0.069 < 0.15 принимаем δe =0,15. 9. Поскольку 1,35/0.36=3.75<4 влияние гибкости панели верхнего пояса на прогиб не учитываем. Рабочая высота сечения: h0 = 0,36 −0,04 = 0,32м . 10. Эксцентриситет продольного усилия относительно растянутой грани сечения:  11. Граничная высота сжатой зоны:  12. Коэффициент относительной величины продольной силы:  13. Определяем относительный изгибающий момент:  14. Параметр δ = as/h0=0.04/0.32 = 0,125. aR=0.390 15. Так как αn > ξR принимаем двойное армирование и значение площади продольной арматуры As и A’s определяем по формуле: Às = 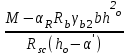 = =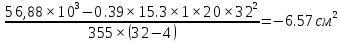 As = 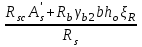 = =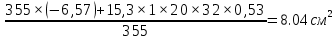 16. Поскольку по расчету сжатая продольная арматура не требуется, то сечение ее назначаем в соответствии с конструктивными требованиями. При гибкости l0/h=1.35/0.36=3.75<5, минимальный процент армирования 0,1%. Тогда получим значение площади продольной арматуры: A’s=0,001bh0=0,001×200×310=62 мм2 . Назначаем армирование сечения верхнего пояса балки: Верхняя арматура 2 Ø7 A’s=77мм2 Нижняя арматура: 2Ø25 As=982 мм2 17. При этом коэффициент продольного армировании составит: 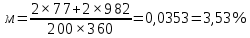 Принятое сечение продольных стержней удовлетворяет конструктивным требованиям. 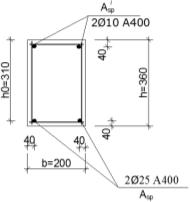 Рис. 6. Подбор продольной сжатой арматуры верхнего пояса Расчет верхнего пояса: наклонное сечение. 1. Усилия в верхнем поясе балки: Q = 98,654 кН, N=1757,75кН. 2. Максимальная поперечная сила в наклонном сечении с учетом перераспределении усилий: Qmax =Q+∆Q= 98.65+49.59= 148.24 кН 3. Параметр Nb =1.3×Rb×103×b×h=1.3×15.3×103×0.2×0.36=1432.08 кН < 1757.75 кН. 4. Коэффициент, учитывающий продольное обжатие: 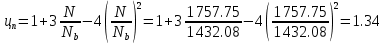 5. Момент в наклонном сечении, воспринимаемый бетоном: 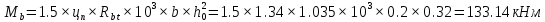 6. Длина проекции наклонного сечения c = 3⋅0,32 = 0,96м >l2=0,7м, то принимаем с = 0,7м 7. Поперечная сила, воспринимаемая бетоном: 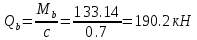 8. Так как Qmax =148.24кН < Qb =190.2 кН, прочность неармированного наклонного сечения обеспечена. Поперечную арматуру устанавливаем конструктивно. 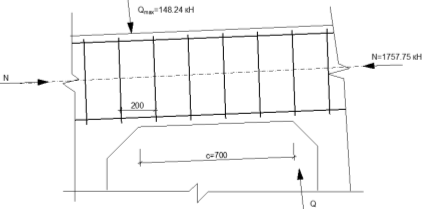 Рис. 7. К расчету верхнего пояса балки по наклонным сечениям 9. Конструктивный шаг поперечных стержней: 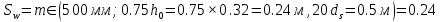 Принимаем поперечную арматуру 2Ø4 В500 с шагом sw=200мм как показано на рис. 7. Подбор продольной арматуры в стойках балки БДР. 1. Расчетные усилия в сечении сжатой стойки: N=17.11кН; M=178.38кНм. Размеры поперечного сечения b=0,2 м; h=0,5 м; величина защитного слоя бетона as=as'=0,04м. Длина панели верхнего пояса l=1,5 м 2. Расчетные сопротивления бетона и арматуры указаны выше. 3. Расчетная длина стойки: l0 =0.8×1,5=1,2м. 4. Определяем величину случайного эксцентриситета: 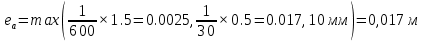 5. Эксцентриситет продольного усилия относительно центра тяжести сечения: 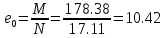 6. Рабочая высота сечения: h0 = 0,5−0,04 = 0,46м . Так как 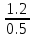 =2.4< 4, т.е. прогиб стойки не учитываем/ =2.4< 4, т.е. прогиб стойки не учитываем/7. Эксцентриситет продольного усилия относительно растянутой грани сечения: 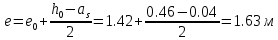 8. Предельный относительный момент при ξR = 0,53: 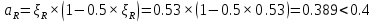 9. Определяем требуемую площадь наиболее сжатой арматуры:  Продольная арматура в сжатой зоне не требуется. 10. Относительный момент:  11. Параметр ξ =1−  0.043 0.04312. Площадь наименее сжатой арматуры:  13. Учитывая конструктивные требования, принимаем нижнюю арматуру 2Ø10 А400 с общей площадью As =157мм2 , ds =10мм , верхнюю 2Ø10А400 As/=157 мм2, ds/ =10мм. 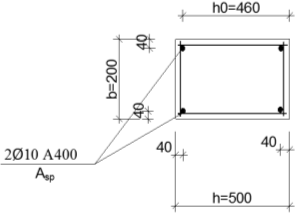 Рис. 8. К расчету прочности сечения стойки Расчет опорного узла. 1. Максимальное поперечное усилие на опоре составляет Qmax=371.52 кН; ширина и высота сечения опорной части b=0,28 м, h1=0,89 м, величина защитного слоя бетона as=as'=0,06 м (см. приложение ) 2. Длина проекции наклонного сечения: c = 2,85м . 3. Рабочая высота сечения: 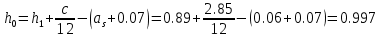 4. Параметр Np=0,7×P=0.7×181.81=127.27кН. 5. Параметр Nb =1.3 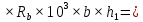 1,3×(15.3×103)×0,2×0.89=3540.42 кН > 127.27кН. 1,3×(15.3×103)×0,2×0.89=3540.42 кН > 127.27кН.6. Коэффициент, учитывающий продольное обжатие: 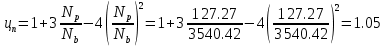 7. Момент, воспринимаемый бетонным сечением: 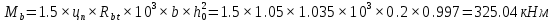 8. Поперечная сила, воспринимаемая бетонным сечением: Qb= 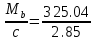 =114.05кН =114.05кН9. Так как Qb=114.05кН > 0,5·1,05·1,035·103·0,2·0,997=108.34кН, т.е. значение Qb не корректируем. 10. Так как Qb=114.05кН < 2,5·1,035·103·0,2·0,997=515.95 кН, то значение поперечной силы Qb не корректируем. 11. Поскольку с =2,85м > 2h0 = 2·0,997 = 1,99м. То принимаем с1 =1,99м. 12. Поперечная сила в таком сечении Q1 = Qmax = 371.52кН 13. Значение параметра: 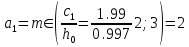 14. Параметр a01 = min(2;2) = 2 . 15. Параметр ε1= 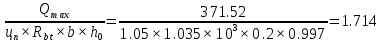 16. Предельное значение параметра: ε 1,ult= 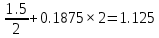 17. Так как ε1=1.714> ε 1,ult=1.125 , тогда требуемая интенсивность хомутов равна: 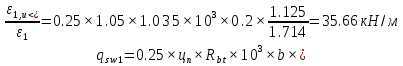 18. qsw=qsw1 = 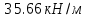 19. Конструктивный шаг поперечных стержней: 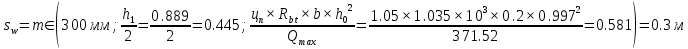 Принимаем шаг поперечных стержней sw=300 мм. 20. Требуемая площадь поперечной арматуры:  21. Принимаем поперечную арматуру 2Ø5 В500 Asw = 39 мм2 с шагом sw=300мм (рис. 9).  Рис. 9. К расчету прочности опорной части балки по наклонному сечению |
