РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ СТЕРЖНЕВОЙ СИСТЕМЫ. Сопромат 1. Расчет статически неопределимой стержневой

• Название: Расчет статически неопределимой стержневой
• Анкор: РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ СТЕРЖНЕВОЙ СИСТЕМЫ
• Дата: 08.05.2022
• Размер: 384.5 Kb.
• Имя файла: Сопромат 1.doc
• Тип: Документы; #518118

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

Санкт-Петербургский Горный Университет



Кафедра механики

Расчетная работа №1

РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ СТЕРЖНЕВОЙ

СИСТЕМЫ

По дисциплине: Сопротивление материавлов _

Выполнил: студент гр. ВД-20 _____________ Красиков М.С.
(подпись) (Ф.И.О)

Проверил: Доцент _____________ Гореликов В.Г.
(должность) (подпись) (Ф.И.О.)

Санкт-Петербург

2022
Таблица 1

Исходные данные.

			d				1	2					Материал стержней
м	м	м	м	м			кН	кН	кН/м		oC	м
2	2	2	2	3	30	30	10	20	10	1		0,001	Медь
											20		Сталь

Таблица 2

Справочные данные.

Материал стержней
	МПа	МПа	oС-1
1. Медь		100
2. Сталь		160

Задание:

Рассчитать площади поперечного сечения стержней конструкции.

Расчетная схема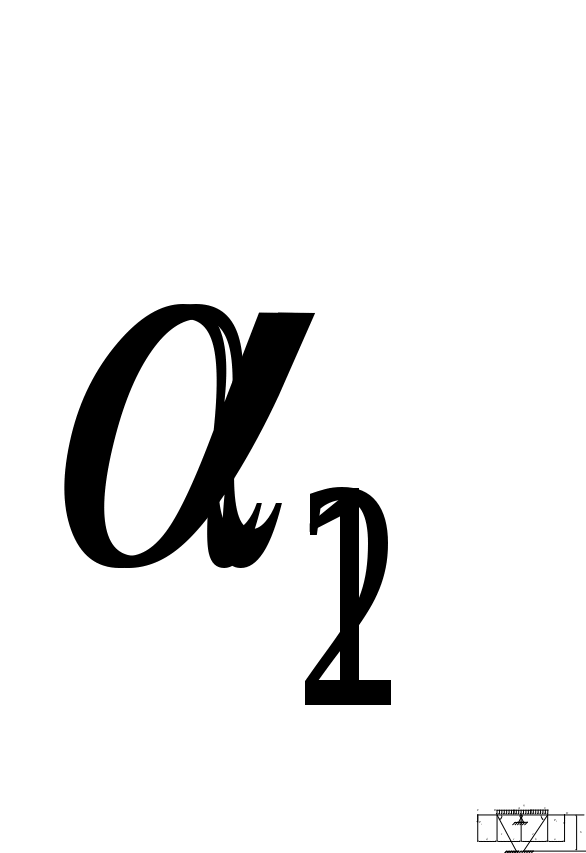




Расчет усилий от внешних сил P₁ P₂ и сосредоточенной нагрузки q.


A

B

C

F


D


Q₁


P₂






P₁

Q₂



h


1

2


b

d

c

a





R₂






R₁
;

Определим, как повернется балка.

.

.

Т.к. , значит, балка повернется вниз (по часовой стрелке).

Составим уравнения статики:

;

и
(1.1)
ли



Таким образом, степень статической неопределимости системы , т.к. имеем два неизвестных усилия и одно уравнение равновесия статики.

Д ля составления условия совместимости деформации необходимо рассмотреть схему перемещений элементов системы.



Составим условие совместности деформаций, используя подобие треугольников .


(1.2)


О
(1.3)
ткуда определим:

;

Подставив равенства (1.3) в формулу (1.2), получим условие совместности деформаций для заданной стержневой системы:


(1.4)


где - безразмерный коэффициент, учитывающий особенности геометрической конфигурации системы.

Используя закон Гука для каждого из стержней, из уравнения (1.4) получим:



Учитывая, что 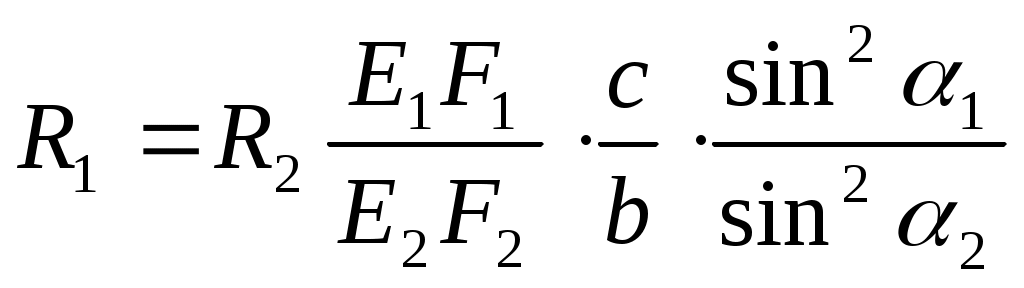и , последнее соотношение моно переписать следующим образом:


(1.5)


Далее решаем совместно систему уравнений (1.1) и (1.5):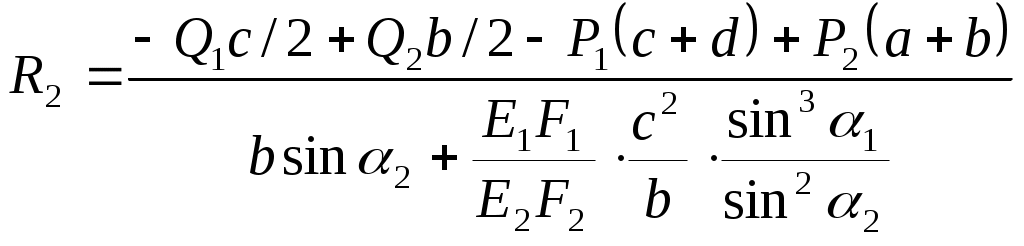









Проверка:

Погрешность

Так как второй стержень работает на сжатие, то окончательно принимаем .

II. Определение напряжений, вызванных неточностью изготовления.



У
(2.1)
равнение равновесия для рассматриваемого случая будет иметь следующий вид:



И
(2.2)
з схемы перемещений получим:

;

Составим условие совместности деформаций, используя подобие треугольников .


(2.3)


О
(2.4)
ткуда определим:

;

Подставив равенства (2.4) в формулу (2.3), получим условие совместности деформаций для заданной стержневой системы:


(2.5)


П
(2.6)
одставим выражения (2.2) в равенство (2.5), получим условие совместимости деформаций:



Используя закон Гука для каждого из стержней, из уравнения (2.6) получим:


(2.7)


Перейдем в уравнении (2.7) к новым переменным, в качестве которых выберем монтажные напряжения

;

Учитывая, что и , последнее соотношение моно переписать следующим образом:


(2.8)


Перепишем уравнение (2.1) в напряжениях:


(2.9)


Решим систему уравнений (2.8) и (2.9) относительно неизвестных напряжений: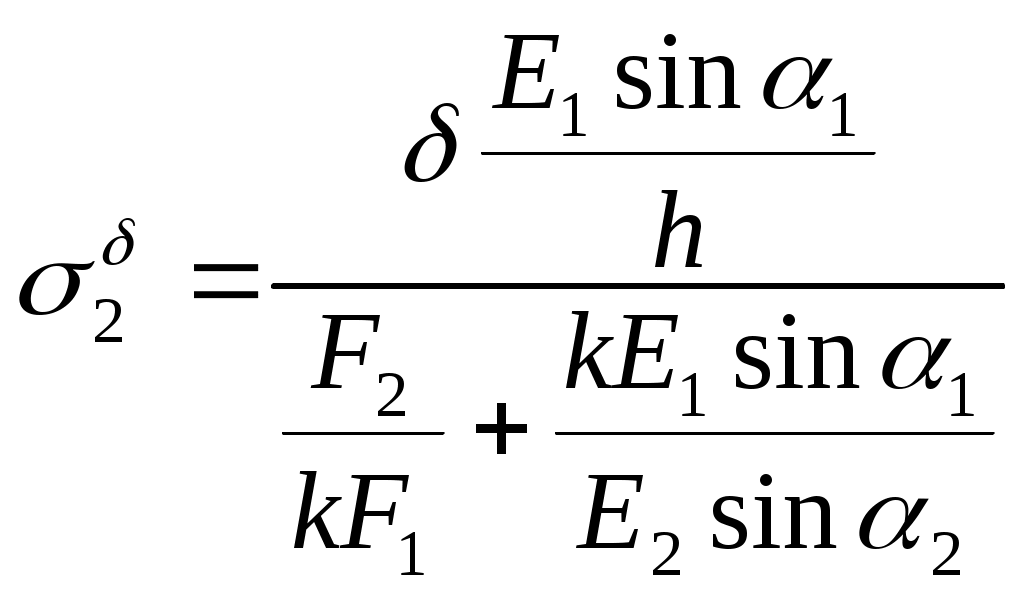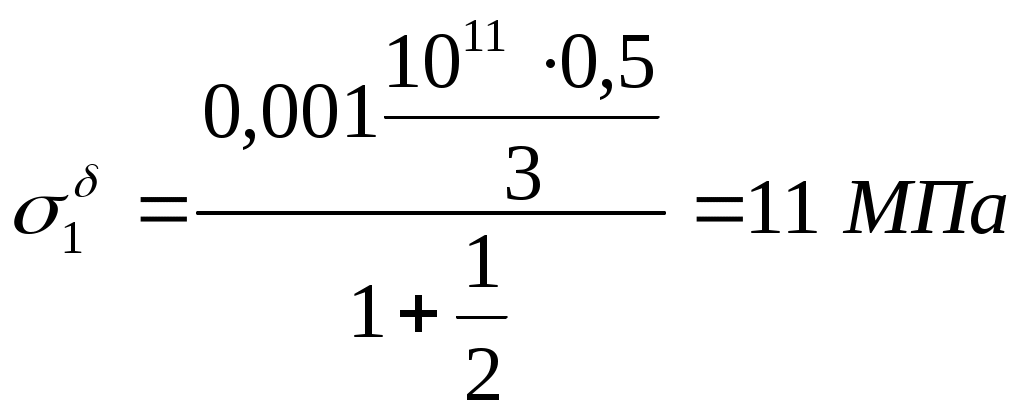











Проверка - верно

Так как оба стержня работают на сжатие, то окончательно принимаем и

3. 
   Расчет температурных напряжений (нагрев).
   

У
(3.1)
равнение равновесия для рассматриваемого случая будет иметь следующий вид:



И
(3.2)
з схемы перемещений получим:

;

где .

Составим условие совместности деформаций, используя подобие треугольников .


(3.3)


О
(3.4)
ткуда определим:

;

Подставив равенства (2.4) в формулу (2.3), получим условие совместности деформаций для заданной стержневой системы:


(3.5)


П
(3.6)
одставим выражения (3.2) в равенство (3.5), получим условие совместимости деформаций:



Используя закон Гука для каждого из стержней, из уравнения (3.6) получим:


(3.7)


Перейдем в уравнении (3.7) к новым переменным, в качестве которых выберем монтажные напряжения

;

Учитывая, что и , последнее соотношение моно переписать следующим образом:


(3.8)


Перепишем уравнение (3.1) в напряжениях:


(3.9)


Решим систему уравнений (3.8) и (3.9) относительно неизвестных напряжений: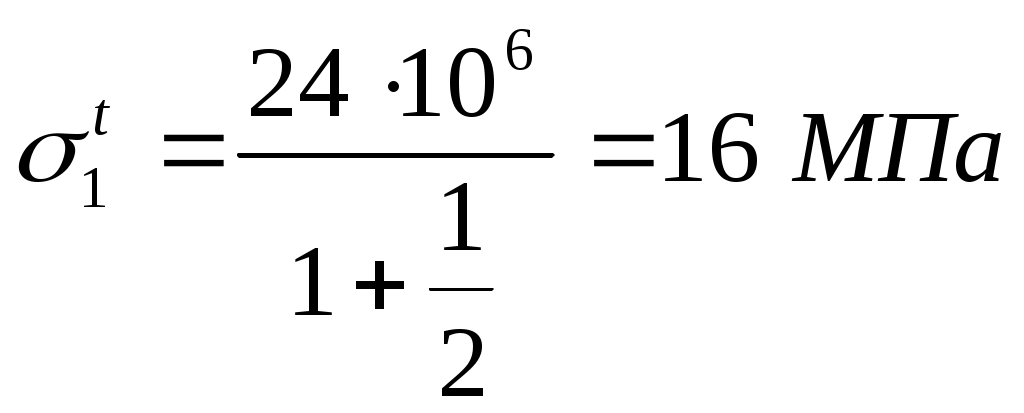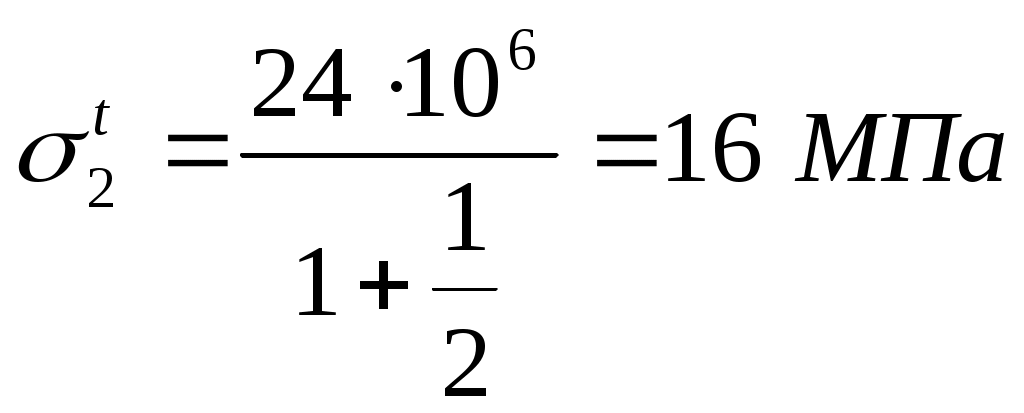











Проверка - верно

Так как оба стержня работают на сжатие, то окончательно принимаем и

3. 
   Подбор сечений элементов систем
   

Таблица 1

Внутренние усилия от сил P и q, МН	Напряжения, МПа
			допускаемые	1

У
(4.1)
словия прочности для каждого из стержней



Тогда


(4.2)






Учитывая заданное отношение , находим площади 1 и 2 стержня соответственно: ; .

Равенству (4.2) удовлетворяет только .

Следовательно, берем

Очевидно, что при этом напряжения в первом стержне будут меньше допустимых, а во втором равны.