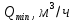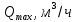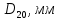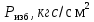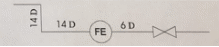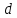Курсач. Курсчианыч. Расчет сужающего устройства расходомера переменного перепада давления
 Скачать 478.79 Kb. Скачать 478.79 Kb.
|
|
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе: и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная. С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии: - z1 и z2 - удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2; - - - удельные кинетические энергии в тех же сечениях. Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна. У 2-2 над плоскостью сравнения; - пьезометрические высоты; В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная. Уравнение Бернулли для реальной жидкости Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3). Потерянная энергия или потерянный напор обозначаются Уравнение Бернулли для реальной жидкости будет иметь вид: 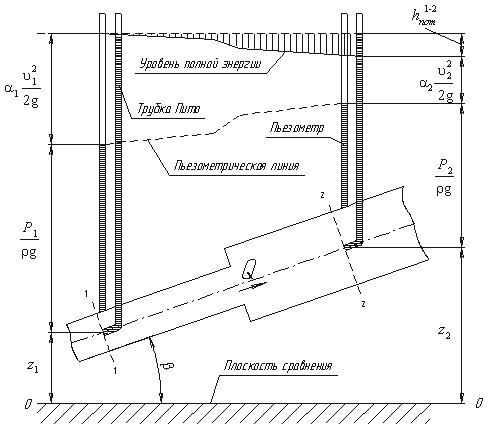 Рис.3 – Схема к выводу уравнения Бернулли для реальной жидкости Из рис.3 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2. Кроме этого, в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости (α=2 для ламинарного режима, α = 1 для турбулентного режима). Потерянная высота 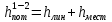 С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ1ω 1 = υ2ω2. 2 Расчетная часть Исходные данные
2.1Определение верхнего предела измерения Выбор верхнего (номинального) предела измерения расхода по шкале дифманометра – расходомера 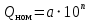 где: 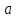 - число из нормального ряда: 1,0; 1,25; 1,6; 2,0; 2,5; 3,2; 4,0; 5,0; 6,3; 8,0 - число из нормального ряда: 1,0; 1,25; 1,6; 2,0; 2,5; 3,2; 4,0; 5,0; 6,3; 8,0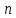 - целое положительное, отрицательное число или ноль. - целое положительное, отрицательное число или ноль.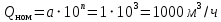 2.2 Расчет и выбор сужающих устройств Конструкция диафрагмы На рисунке показано поперечное сечение диафрагмы. Буквенные обозначения составных частей и геометрических размеров диафрагмы, приведенные на рисунке 3, использованы далее в настоящем разделе. 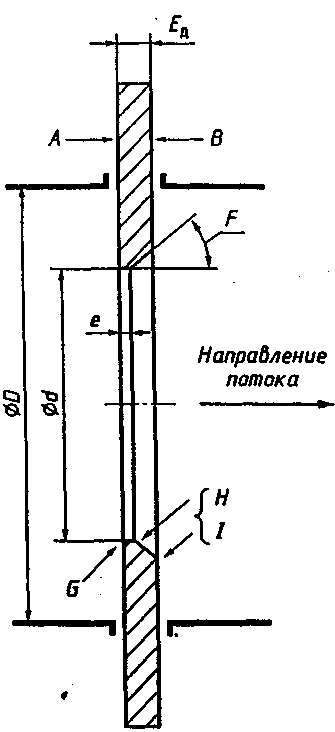 Рис. –4 Стандартная диафрагма Определим число Рейнольдса, которое характеризует отношение силы инерции к силе вязкости потока: 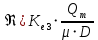 где 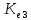 - масштабный коэффициент, значения которого приведены в таблице А.6 (ГОСТ 8.563.2 – 97). - масштабный коэффициент, значения которого приведены в таблице А.6 (ГОСТ 8.563.2 – 97).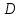 - измеряется в [м], - измеряется в [м], 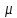 - - 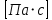 , , 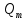 - [м3/ч]. - [м3/ч]. Для таких размерностей определим коэффициент 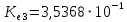 . .Динамическая вязкость воды равна 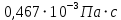 Плотность воды равна 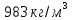 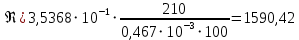 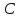 - коэффициент истечения - коэффициент истечения Коэффициент истечения определяют по уравнению Штольца: 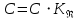 , ,где 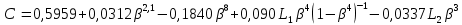 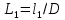 - отношение расстояния от входного торца диафрагмы до оси - отношение расстояния от входного торца диафрагмы до осиотверстия для отбора давления перед диафрагмой к диаметру ИТ; 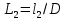 - отношение расстояния от выходного торца диафрагмы до оси отверстия для отбора давления за диафрагмой к диаметру ИТ. - отношение расстояния от выходного торца диафрагмы до оси отверстия для отбора давления за диафрагмой к диаметру ИТ.В уравнении значения 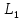 и и 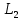 принимают равными: принимают равными:для углового отбора давления 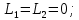 Следовательно: 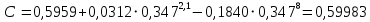 Следовательно: 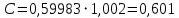 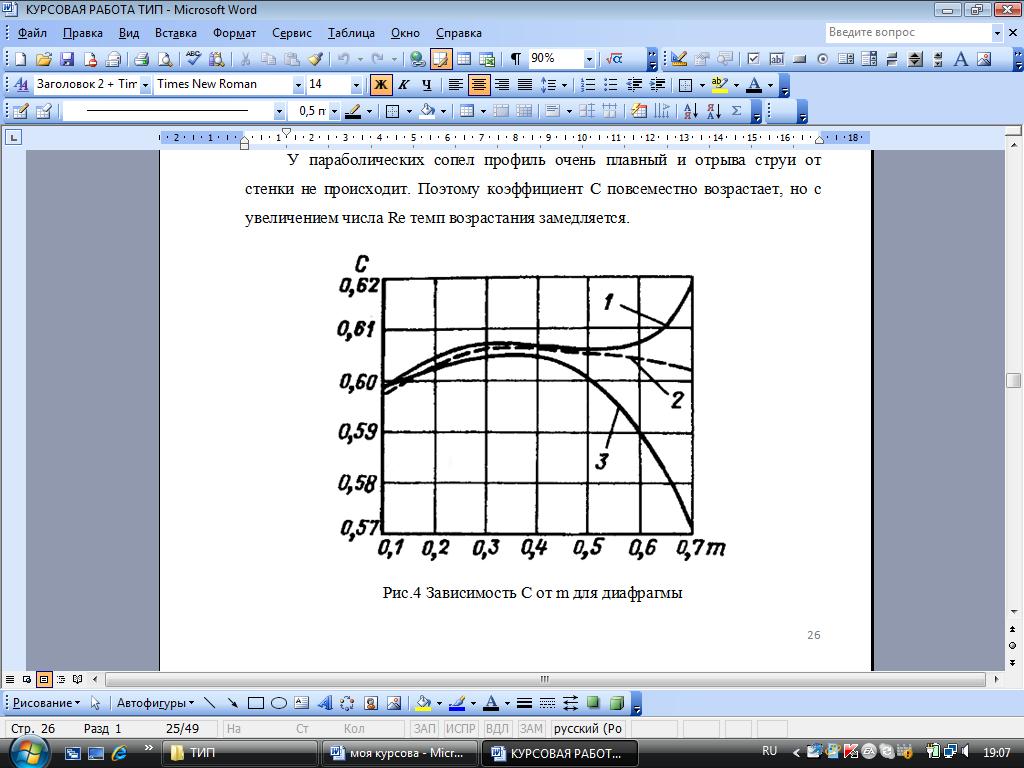 Рис. 5 – Зависимость коэффициента истечения 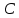 от от 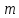 диафрагмы при отборах: 1 – радиальном, 2 – по методу суженой струи, 3 – угловом. диафрагмы при отборах: 1 – радиальном, 2 – по методу суженой струи, 3 – угловом.Относительная площадь СУ: 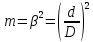 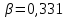 О 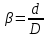 тносительный диаметр отверстия СУ: тносительный диаметр отверстия СУ:Откуда:
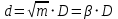 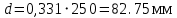 Выберем стандартную диафрагму с угловым методом отбора давления. Стандартные диафрагмы применяют при следующих условиях: - диафрагмы с угловым отбором давления: 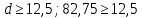 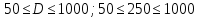 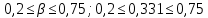 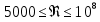 при при 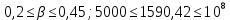 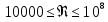 при при 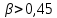 2.3 Расчет потери напора Потеря давления представляет собой разность статических давлений у стенки ИТ: - измеренного перед СУ в месте, где становится пренебрежимо малым влияние давления (приблизительно 1D), обусловленного торможением входящего потока непосредственно у диафрагмы. - измеренного за СУ в месте, где можно считать полностью законченным процесс восстановления статического давления, обусловленного расширением струи (приблизительно 6D за СУ). Потерю давления можно определить по графику: 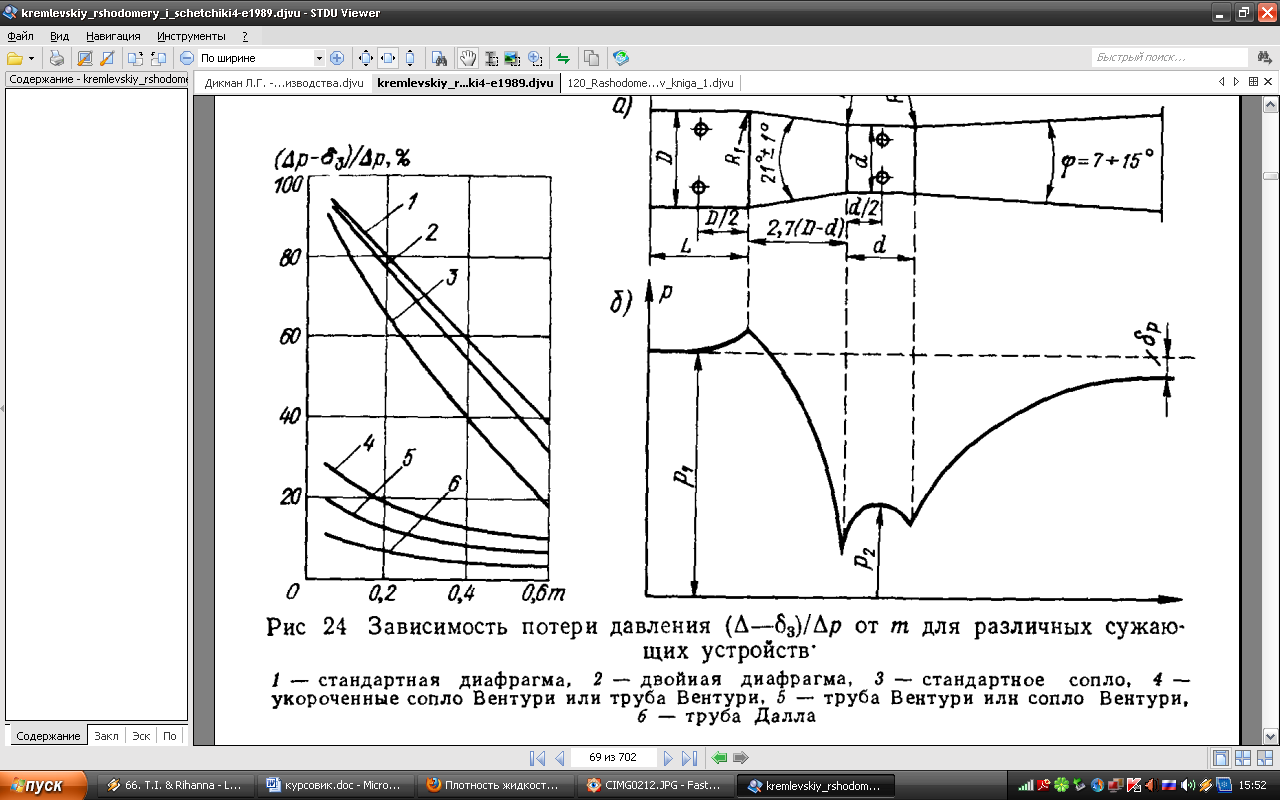 Рис. 6 – Зависимость потерь давления от m в различных сужающих устройствах: 1- диафрагма; 2 – сопло; 3- короткое сопло Вентури; 4 – длинное сопло Вентури 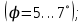 5 – длинное сопло Вентури 5 – длинное сопло Вентури 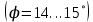 При 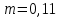 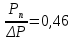 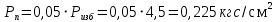 Отсюда можно определить перепад давления 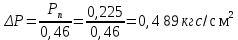 Значение 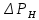 выбираем из ряда нормальных перепадов давлений по ГОСТ 18140-84: выбираем из ряда нормальных перепадов давлений по ГОСТ 18140-84: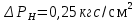 2.4 Расчет поправочного коэффициента на шероховатость 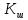 Шероховатость трубопровода при определении ее влияния на коэффициент истечения СУ оценивают по эквивалентной шероховатости 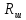 . Для расчета диафрагмы в качестве материала ИТ была выбрана сталь 12МХ. Примем внутреннюю поверхность трубопровода новая сварная. Для такого состояния поверхности значение эквивалентной шероховатости . Для расчета диафрагмы в качестве материала ИТ была выбрана сталь 12МХ. Примем внутреннюю поверхность трубопровода новая сварная. Для такого состояния поверхности значение эквивалентной шероховатости 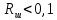 (ГОСТ 8.563.1-97 таблица Б.1). (ГОСТ 8.563.1-97 таблица Б.1).Коэффициент на шероховатость внутренней поверхности ИТ при относительной шероховатости 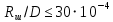 определяют по формуле определяют по формуле 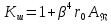 где 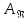 при при 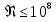 для диафрагм 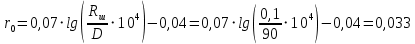 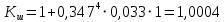 2.5 Расчет коэффициента на притупление входной кромки диафрагмы 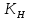 Поправочный коэффициент на притупление входной кромки при 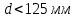 определяют по формуле определяют по формуле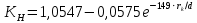 где 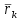 - средний за межповерочный интервал радиус закругления входной кромки диафрагмы. - средний за межповерочный интервал радиус закругления входной кромки диафрагмы.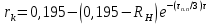 где  - межповерочный интервал, годы; - межповерочный интервал, годы;При этом следует иметь в виду, при 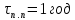 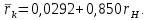 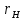 - начальное значение радиуса закругления входной кромки диафрагмы. Если экспериментальное определение начального радиуса закругления не представляется возможным, то его принимают равным 0,05мм. - начальное значение радиуса закругления входной кромки диафрагмы. Если экспериментальное определение начального радиуса закругления не представляется возможным, то его принимают равным 0,05мм.Следовательно: 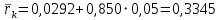 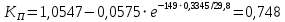 2.6 Определение действительного расхода Уравнение массового расхода в общем случае имеет вид (ГОСТ 8.563.1 – 97 пункт 5.3): 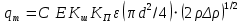 E – коэффициент скорости входа 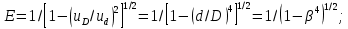 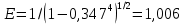 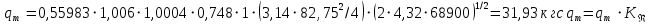 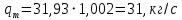 2.7 Выбор дифманометра Выбор дифманометра, работающего в комплекте с сужающим устройством, в основном сводится к определению номинального перепада давления согласно стандартной шкале перепадов. Если потеря давления в сужающем устройстве не имеет значения, перепад выбирают таким, что бы модуль был равен 0,2, так как большее уменьшение модуля (следовательно, повышения перепада давления), как правило, нецелесообразно. Если же задана допустимая потеря давления в сужающем устройстве, то принимают такое наибольшее значение номинального перепада давления дифманометра, при котором потеря давления еще остается меньше допустимой. Выберем манометр дифференциальный показывающий ДСП-160-М1. Дифференциальный манометр (дифманометры) предназначены для измерения: а) расхода жидких и газообразных сред по методу переменного перепада давления в стандартных сужающих устройствах (расходомеры); б) разности давлений жидких и газообразных сред (перепадомеры); в) уровня жидких сред, находящихся под атмосферным, вакуумметрическим или избыточным давлением (уровнемеры). Технические характеристики: Предельно допускаемые рабочие избыточные давления, кгс/см: 0,25; 0,4; 0,63; 1,0; 1,6; 2,5; 4,0; 6,3 Предельные номинальные перепады давлений, | |||||||||||||||||||||||||||||||||