Л3 - Расчет тангенса угла магнитных потерь. Расчет тангенса угла магнитных потерь
 Скачать 126.28 Kb. Скачать 126.28 Kb.
|
|
Лабораторная работа РАСЧЕТ ТАНГЕНСА УГЛА МАГНИТНЫХ ПОТЕРЬ Цель работы – изучить зависимость тангенса угла магнитных потерь катушки индуктивности с сердечником от частоты и величины приложенного напряжения. 1.1 Тангенс угла магнитных потерь При перемагничивании в переменном поле имеет место отставание по фазе магнитной индукции от напряженности магнитного поля. Происходит это в результате действия вихревых токов, препятствующих, в соответствии с законом Ленца, изменению магнитной индукции, а также из-за гистерезисных явлений и магнитного последействия. Угол отставания называют углом магнитных потерь и обозначают δм. Для характеристики динамических свойств магнитных материалов используют тангенс угла магнитных потерь tg δм. На рис. 1 представлены последовательная эквивалентная схема замещения и векторная диаграмма тороидальной катушки индуктивности с сердечником из магнитного материала, где сопротивление r1 эквивалентно всем видам потерь мощности в катушке с сердечником. 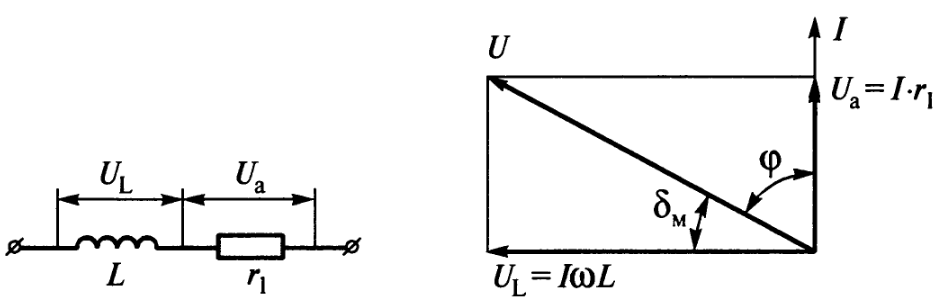 Рис. 1 – Эквивалентная схема замещения и векторная диаграмма катушки индуктивности с магнитным сердечником Если пренебречь сопротивлением обмотки катушки и ее собственной емкостью, то из векторной диаграммы получим 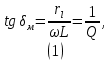 где ω – угловая частота; L – индуктивность катушки; Q – добротность катушки с испытуемым магнитным материалом. Выражение (1) показывает, что тангенс угла магнитных потерь является величиной, обратной добротности катушки. 1.2 Особенности расчёта индуктивных элементов с сердечниками Магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость. Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения 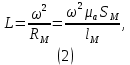 где ω – количество витков катушки, RM – сопротивление магнитной цепи, μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник, SM – площадь поперечного сечения сердечника, lM – длина средней магнитной силовой линии. Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %. Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле 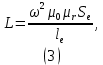 где ω – количество витков катушки, μ0 – магнитная постоянная, μ0 = 4π10-7, μr – относительная магнитная проницаемость вещества, Se – эффективная площадь поперечного сечения сердечника, le – эффективный путь магнитной линии сердечника. Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников: С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечному сечению сердечника, измеряется в мм-1; С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3. 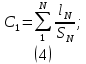 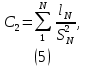 где N – количество разнородных участков сердечника, lN – длина N – го участка сердечника, SN – площадь N – го участка сердечника. Тогда величины Se и le определятся из следующих выражений 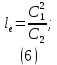 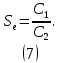 Кроме индуктивности с помощью постоянных С1 и С2 определяют эффективный объём Ve, который требуется для определения параметров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению 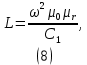 где ω – количество витков катушки, μ0 – магнитная постоянная, μ0 = 4π10-7, μr – относительная магнитная проницаемость вещества, С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечному сечению сердечника. Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое. 1.3 Расчёт катушки с тороидальным сердечником Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях. Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D1 – внешний диаметр, D2 – внутренний диаметр, h – высота сердечника (рис. 2). 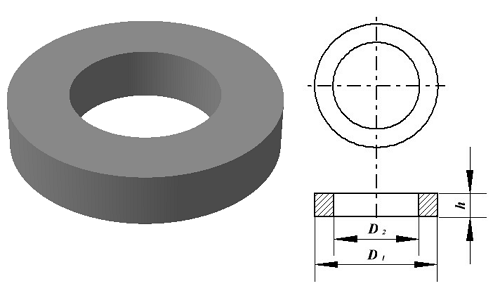 Рис.2 – Тороидальный сердечник Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют 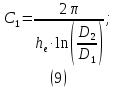 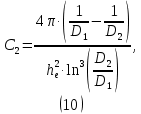 где he – эффективная высота сердечника, D1 – внешний диаметр сердечника, D2 – внутренний диаметр сердечника. Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей (рис. 3). 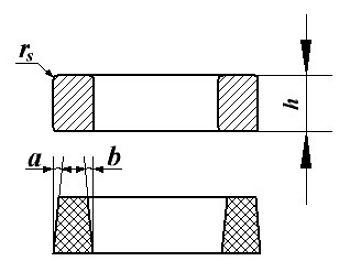 Рис. 3 – Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу) Рассмотрим несколько случаев: а) прямоугольное поперечное сечение с острыми кромками 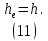 б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления rs 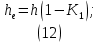 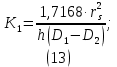 в) трапецеидальное поперечное сечение с острыми кромками 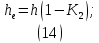 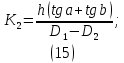 г) трапецеидальное поперечное сечение со скруглёнными кромками 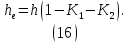 Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000. 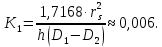 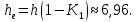 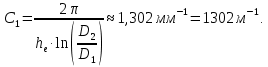 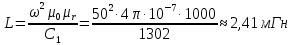 1.4 Сопротивление катушки индуктивности Сопротивление катушки индуктивности включает две составляющих: индуктивное сопротивление; сопротивление потерь. Индуктивное сопротивление (реактивное сопротивление, импеданс) зависит от частоты протекающего тока: 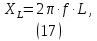 где f – частота; L – индуктивность. Сопротивление потерь включает в себя: потери в проводах (активное сопротивление катушки); потери на вихревые токи; потери в сердечнике; потери в диэлектрике. Некоторые потери вносит также распределенная емкость, которую снижают путем использования особой конфигурации обмоток, разделения ее на секции. Основную долю потерь вносит активное сопротивление. Активное сопротивление обуславливается омической характеристикой проводов обмотки. При работе на низких частотах омическое сопротивление не зависит от частоты. В мощных устройствах необходимо учитывать эффект близости, который заключается в том, что токи и образуемое ими магнитное поле вызывают вытеснение тока в проводах соседних витков. В результате снижается эффективное используемое сечение провода и растет его омическое сопротивление. Во многих случаях применения катушек индуктивности следует учитывать влияние активного сопротивления обмоток. Данный параметр может отрицательно влиять не только путем снижения добротности, но и вызывать повышенный нагрев проводников обмоток в том случае, когда устройство работает с большими токами. Пример. Рассчитать активное сопротивление однорядой круглой катушки: число витков: ω = 10; внутренний диаметр катушки Dk = 10 мм; диаметр медного провода dпр = 0,5 мм. Активное сопротивление любого проводника определяется: 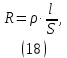 где ρ = 1,7∙10-8 Ом∙м – удельная проводимость материала (в данном случае - меди), l – длина проводника, м, S – площадь поперечного сечения проводника, м2. Определим длину проводника. Для этого рассчитаем длину витка и умножим её на число витков. При этом длина витка будет равна длине окружности: 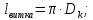 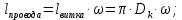 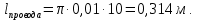 Определим площадь поперечного сечения проводника. будем условно считать, что катушка намотана проводником прямоугольного сечения. В этом случае площадь поперечного сечения проводника будет определяться: 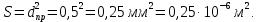 Определим сопротивление обмотки: 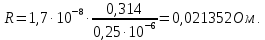 2 Практическая часть 1.1 Рассчитать индуктивность тороидальной катушки по параметрам, взятым из таблицы 1. 1.2 Рассчитать сопротивление катушки индуктивности. В качестве материала провода взять медь (ρ = 1,7∙10-8 Ом∙м). 1.3 В программе Qucs построить эквивалентную схему замещения катушки индуктивности с магнитным сердечником (рис.1). В качестве параметров индуктивности и сопротивления ввести рассчитанные значения. 1.4 Смоделировать падения напряжения на них при различной величине приложенного напряжения (от 100 В до 1000 В) и различной его частоте (от 50 Гц до 1000 Гц). 1.5 По измеренным значениям падения напряжения рассчитать тангенс угла магнитных потерь используя формулу (1). 1.6 Построить зависимость тангенса угла магнитных потерь от частоты. 1.7 Повторить расчеты 1.1 – 1.6 увеличив значение относительной магнитной проницаемость сердечника из табл. 1 на 50 %, затем на 100 %. 1.8 Повторить расчеты 1.1 – 1.6 уменьшив значение относительной магнитной проницаемость сердечника из табл. 1 на 50 %, затем на 75 %. 1.9 По полученным данным построить зависимость тангенса угла магнитных потерь при частоте 50 Гц от относительной магнитной проницаемости сердечника. 1.10 Объяснить полученные зависимости с физической точки зрения. Таблица 1 – Параметры тороидальной катушки со скруглёнными кромками, радиус скругления 0,4 мм, сечение магнитопровода прямоугольное
|
