Расчет теплопроводности магнитной жидкости. Рубачев. Расчет теплоемкости и теплопроводности магнитных жидкостей
 Скачать 61.31 Kb. Скачать 61.31 Kb.
|
|
РАСЧЕТ ТЕПЛОЕМКОСТИ И ТЕПЛОПРОВОДНОСТИ МАГНИТНЫХ ЖИДКОСТЕЙ Рубачев В.В, Яновский А.А. Ставропольский государственный аграрный университет Ставрополь, Россия CALCULATION OF HEAT AND THERMAL CONDUCTIVITY IN THE MAGNETIC FLUIDS Rubachev V.V., Yanovsky A.A. Stavropol State Agrarian University Stavropol, Russia К настоящему времени вполне апробированы технические устройства (муфты, тормоза, амортизаторы, управляемые магнитным полем), в которых магнитные жидкости используются в качестве рабочего тела [1]. Но данные механизмы работают при температуре 60-80⁰С, поэтому важно знать, как поведет себя магнитная жидкость при еще большем росте температуры [2-10]. Для этого необходимо рассчитывать значения эффективной вязкости, теплоемкости и теплопроводности магнитных жидкостей. Первоначально температурная зависимость вязкости разбавленных магнитных жидкостей принималась равной зависимости вязкости жидкой основы от температуры. Исторически этот подход был связан с первой простейшей физико-математической моделью магнитной жидкости, которая описывала течение однородного жидкого магнетика с независящей от магнитного поля вязкостью. При этом не рассматривались два существенных обстоятельства. Во-первых, в жидкой основе растворён некоторый объём поверхностно-активного вещества, «искажающего» ее переносные свойства. Во-вторых, вязкость магнитной жидкости является эффективной величиной, зависящей от ряда диссипативных механизмов, которые отсутствуют в гомогенной жидкости. Их влияние на эффективную вязкость может тоже зависеть от температуры, например вклад вращательной вязкости. В состоянии насыщения (∆η ͚) угловая скорость каждой частицы равна нулю и действующий момент сил вязкого трения деформирует слой поверхностно-активного вещества. Поэтому температурная зависимость эффективной вязкости магнитной жидкости при течении в магнитном поле может оказаться ближе к температурной зависимости вязкости ПАВ, чем при течении без поля. Вискозиметрические опыты Г.Э. Кронкалнса, М.М. Майорова, В.Е. Фертмана (1984)подтвердили высказанные выше соображения: температурная зависимость эффективной вязкости, соответствующей линейному участку кривой течения (γ>10³с¯¹), концентрированных магнитных жидкостей на углеводородных основаниях отличалась от температурной зависимости вязкости основы. Эти данные качественно согласуются с результатами К. Судоу (K.Sudou) и др. (1987), измеривших эффективную вязкость магнитной жидкости на основе воды для двух концентраций частиц магнетита, и В.Г. Гилеева, А.Л. Спириной, Е.Г Фадеевой (1987), исследовавших магнитные жидкости на основе керосина. Эффективный коэффициент вязкости магнитной жидкости на основе керосина (M ͚=24кА/м) при скорости сдвига γ=1312с¹ в интервале температур - 40-30⁰C удовлетворительно описывается формулой Андраде (H=0) ( Г.Э. Кронкалнс и др., 1984): 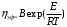 (1) (1)где B=5.9·10¯³мПа·с; E=15.8кДж/моль; R=8.31Дж/(моль·К) (R – газовая постоянная) . При измерении температурной зависимости вязкости близких по характеристикам магнитных жидкостей на основе керосина в интервале t=20-80⁰C получены значения E=17,54 кДЖ/моль, B=5,58·10-3 МПа·с (З. Гропсиан (Z. Gropsian) и др., 1985). В этом же интервале температур вязкость керосина и олеиновой кислоты описывается зависимостью (1) при 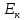 =12.74 кДж/моль, =12.74 кДж/моль, 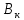 =8,45·10-3 МПа·с и =8,45·10-3 МПа·с и 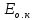 =21,95 кДж/моль, =21,95 кДж/моль, 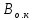 =3,84·10-3 МПа·с соответственно. =3,84·10-3 МПа·с соответственно.В упоминавшейся работе В.Г. Гилева, А.Л. Спириной и Е.Г. Фадеевой измерена также зависимость Е от напряженности магнитного поля Н, которая для магнитной жидкости с концентрацией ϕ=0,32 стремилась к насыщению в области Н>600кА/м. Анализ известных экспериментальных данных, полученных для магнитных жидкостей на углеводородных основах и обработанных в виде (1), показал сильную зависимость Е и В от величины исследованного температурного интервала. Как правило, погрешность аппроксимации температурной зависимости эффективной вязкости формулой (1) неограниченно возрастала у границ интервала. Эту тенденцию удалось исключить при аппроксимации экспериментальных данных зависимостью 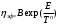 (2) (2)При этом относительная погрешность аппроксимации оказалась в несколько раз ниже, чем при аппроксимации, и не превышала 2 % в интервале Т=290-350 К. Для удобства сравнения известных результатов целесообразно формулу (1) привести к следующему виду: 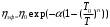 (3) (3)где ηₒ=η(Тₒ); α=lnK (K – отношение вязкостей 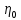 /η(T /η(T 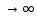 )); Tₒ - характерная температура; n - константа. )); Tₒ - характерная температура; n - константа.Из соотношений (2) и (3) следуют выражения для коэффициентов: 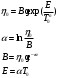 (4) (4)Для сравнения температурной зависимости вязкости магнитных жидкостей на различных основах Т. должно поддерживаться постоянным, например 293 К. Безразмерный коэффициент вязкости ῆ=η/ηₒ из формулы (3) запишется в виде 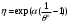 , (5) , (5)где 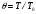 При обработке известных вискозиметрических данных с помощью соотношения (4) получены следующие границы изменения коэффициенов: К=3-20; n=1-3,5 при Тₒ 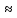 293 К. 293 К.Магнитные жидкости с умеренной концентрацией твердой фазы при отсутствии магнитного поля не проявляли неньютоновских свойств. Однако в магнитном поле наблюдается зависимость эффективной вязкости не только от температуры, но и от скорости сдвиговой деформации. Таким образом, в слабых магнитных полях оба механизма (агрегатирование и увлечение частиц вихревым потоком), определяющие зависимость 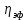 (γ), проявляются при одних и тех же скоростях сдвиговой деформации и разделить действия этих механизмов практически невозможно. С увеличением напряженности магнитного поля растут скорости сдвиговой деформации, при которых исчезает вращательная вязкость. В то же время та область γ, где на характер течения жидкости сильно влияет агрегатирование, по прежнему ограничена: γ˂10³с¹ .Поэтому результаты измерений эффективной вязкости магнитной жидкости при больших напряженностях поля (Н (γ), проявляются при одних и тех же скоростях сдвиговой деформации и разделить действия этих механизмов практически невозможно. С увеличением напряженности магнитного поля растут скорости сдвиговой деформации, при которых исчезает вращательная вязкость. В то же время та область γ, где на характер течения жидкости сильно влияет агрегатирование, по прежнему ограничена: γ˂10³с¹ .Поэтому результаты измерений эффективной вязкости магнитной жидкости при больших напряженностях поля (Н 10³ А/м) и высоких скоростях сдвиговой деформации (γ>10³с¹) позволяют найти температурную зависимость вращательной вязкости. 10³ А/м) и высоких скоростях сдвиговой деформации (γ>10³с¹) позволяют найти температурную зависимость вращательной вязкости.Наличие твердой фазы в магнитной жидкости увеличивает ее теплопроводность, так как коэффициент теплопроводности магнетита в среднем более чем на порядок превышает теплопроводность используемых жидких основ. Например, при комнатной температуре коэффициент теплопроводности магнетита 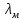 , по справочным данным, приблизительно равен 10 Вт/ (м·К), а вакуумного масла ВМ-1—0,13 Вт/ (м·К). , по справочным данным, приблизительно равен 10 Вт/ (м·К), а вакуумного масла ВМ-1—0,13 Вт/ (м·К).В настоящее время отсутствуют надежные опытные данные о влиянии магнитного поля на теплопроводность магнитных жидкостей: в большинстве экспериментов влияния полей Н 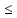 200 кА/м не обнаружено. 200 кА/м не обнаружено.Одна из первых формул для расчета теплопроводности коллоидных растворов была получена Б.М. Тареевым (1940) по аналогии с расчетом электрического поля в двухфазной системе: 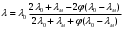 , (6) , (6)где λₒ и 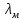 - коэффициенты теплопроводности жидкой и твердой фаз соответственно. - коэффициенты теплопроводности жидкой и твердой фаз соответственно.Обобщив известные экспериментальные данные для магнитных жидкостей на углеводородной основе в диапазоне 0,004 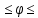 0,2 зависимостью вида 0,2 зависимостью вида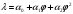 , (2.37) , (2.37)Среднее квадратичное отклонение опытных точек от этой зависимости (кривая 3) составляет 3%, а максимальное отклонение не превышает 6%. Зависимость теплопроводности магнитной жидкости от температуры определяется концентрацией дисперсной фазы, 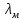 (t)которой отличается от λₒ(t) жидкой фазы. Анализ известных опытных данных показывает, что с ростом температуры наблюдается линейное падение эффективного коэффициента теплопроводности магнитных жидкостей. В связи с тем, что температурные коэффициенты жидкой и твердой фаз различны, коэффициент теплопроводности магнитной жидкости с ростом температуры все меньше отличается отличается от λₒ: от 30% при комнатной температуре до 17% при 90⁰С. (t)которой отличается от λₒ(t) жидкой фазы. Анализ известных опытных данных показывает, что с ростом температуры наблюдается линейное падение эффективного коэффициента теплопроводности магнитных жидкостей. В связи с тем, что температурные коэффициенты жидкой и твердой фаз различны, коэффициент теплопроводности магнитной жидкости с ростом температуры все меньше отличается отличается от λₒ: от 30% при комнатной температуре до 17% при 90⁰С.Обобщенная формула температурной зависимости коэффициента теплопроводности магнитной жидкости может быть представлена в виде 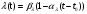 , (8) , (8)где 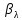 и и 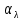 - коэффициенты, зависящие от теплопроводности жидкой фазы и магнетита, а также от его концентрации, tₒ характерная температура. - коэффициенты, зависящие от теплопроводности жидкой фазы и магнетита, а также от его концентрации, tₒ характерная температура.Коэффициенты 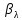 и и 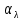 для концентрированных магнитных жидкостей можно определить линеаризацией соотношения (6), предполагая справедливость закона (7) для λₒ и для концентрированных магнитных жидкостей можно определить линеаризацией соотношения (6), предполагая справедливость закона (7) для λₒ и 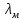 Запишем выражение в виде Запишем выражение в виде 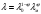 После линеаризации уравнения (7) получим: 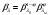 ; ;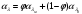 , (9) , (9)где 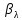 , ,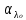 , , 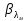 , , 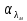 – коэффициенты, характеризующие температурную зависимость теплопроводности жидкой фазы и магнетита соответственно. – коэффициенты, характеризующие температурную зависимость теплопроводности жидкой фазы и магнетита соответственно.В связи с отсутствием справочных данных по температурной зависимости магнетита можно использовать соотношение 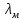 (t)=8.0(1-5.6·10¯³(t-20)), (10) (t)=8.0(1-5.6·10¯³(t-20)), (10)которое получено путем сравнения опытных данных по λ(t) и λₒ(t). Влияние процессов, происходящих в твердых частицах при переходе ферромагнитной фазы в парамагнитную, на теплоемкость магнитной жидкости может наблюдаться только при таких температурах, когда существование магнитной жидкости как физического объекта проблематично. Выполненные оценки дают основание также не учитывать влияние на теплоемкость дипольного взаимодействия частиц. Эксперименты А.Е. Венгер и др. (1984) показали, что при расчете теплоемкости магнитной жидкости в интервале температур 47-97*С можно использовать правило смешения. Температурная зависимость теплоемкости высококонцентрированной магнитной жидкости на основе трансформаторного масла (ϕ=0,26) аппроксимировалась линейной зависимостью с коэффициентом корреляции 0,997: 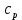 = 1,088+0,227·10-² (Т-273) где с - удельная теплоемкость, кДж/(кг·К). = 1,088+0,227·10-² (Т-273) где с - удельная теплоемкость, кДж/(кг·К).Снижение теплоемкости высококонцентрированной жидкости по сравнению с теплоемкостью основы обусловлено большим содержанием дисперсного магнетита, теплоемкость которого при исследованных температурах составляет 0,654 – 0,712 кДж/(кг·К). Измерения показали [1], что при расчете удельной теплоемкости концентрированной магнитной жидкости (ϕ  0,2) можно использовать следующее соотношение: 0,2) можно использовать следующее соотношение: 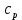 =0 ,425+0,135·10²l+0,345 =0 ,425+0,135·10²l+0,345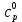 (11) (11)Отклонения от линейной зависимости 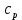 (t) в области отрицательных температур трактовались Э.М. Агабекяном и др. (1987) как фазовый переход первого рода, при котором происходит объединение магнитных частиц в кластеры с нулевым суммарным магнитным моментом. (t) в области отрицательных температур трактовались Э.М. Агабекяном и др. (1987) как фазовый переход первого рода, при котором происходит объединение магнитных частиц в кластеры с нулевым суммарным магнитным моментом.Список литературы Фертман В.Е. Магнитные жидкости: Справочное пособие. Минск: Высш. шк. 1988. 184 с. Яновский А.А. А.Я. Симоновский, Холопов В.Л. Влияние магнитного поля на процессы парообразования в кипящей магнитной жидкости // Фундаментальные исследования. 2013. № 8-2. С. 332-337. Яновский А.А. Тепло- и массоперенос при кипении магнитной жидкости на неограниченной поверхности с точечным подводом тепла / Вестник Нижегородского университета им. Н.И. Лобачевского. 2011. № 4-3. С. 1289-1290. Симоновский А.Я., Яновский А.А. Влияние однородного магнитного поля на теплообмен при кипении магнитной жидкости на неограниченной поверхности // Наука. Инновации. Технологии. 2011. № 6-1. С. 272-278. Игропуло В.С., Яновский А.А. Математическое моделирование некоторых ориентационных процессов на наноповерхностях // Обозрение прикладной и промышленной математики. 2008. т. 15. № 3. C. 484-485. Теплообмен в кипящей магнитной жидкости / Яновский А.А., Симоновский А.Я., Холопов В.Л. // В сборнике: Физико-химические и прикладные проблемы магнитных дисперсных наносиcтем V Всероссийская научная конференция с международным участием: сборник начных трудов. 2015. С. 276-282. Моделирование отрыва пузырьков пара в кипящей магнитной жидкости / Яновский А.А., Симоновский А.Я., Холопов В.Л. // В сборнике: Физико-химические и прикладные проблемы магнитных дисперсных наносиcтем V Всероссийская научная конференция с международным участием: сборник начных трудов. 2015. С. 239-246. Математическое моделирование и разработка систем охлаждения процессоров персональных компьютеров / Яновский А.А., Каныгин Я.В. // Международный студенческий научный вестник. 2015. № 3-4. С. 496-498. Перспективы развития и моделирования систем охлаждения процессоров пк с использованием магнитной жидкости в качестве охлаждающей среды / Яновский А.А., Симоновский А.Я., Хаустов П.А. // Международный студенческий научный вестник. 2015. № 3-4. С. 498-499. Математическое моделирование процесса образования пузырька пара в магнитной жидкости / Козлова В.Р., Бородина Е.С., Яновский А.А., Симоновский А.Я. // Международный студенческий научный вестник. 2016. № 3-3. С. 386-387. |
