Расчет транзисторного автогенератора с кварцевым резонатором
 Скачать 491.21 Kb. Скачать 491.21 Kb.
|
|
1.3. Особенности проектирования кварцевых автогенераторов 1.3.1. Эквивалентная схема кварцевого резонатора Стабильность частоты автогенератора в основном определяется эталонными свойствами и добротностью его колебательной системы. Эталонные свойства и добротность электрических колебательных систем (LC -контуров) обычно ограничивают относительную нестабильность частоты АГ значением порядка 10−4. В тех случаях, когда требуется более высокая стабильность частоты, в АГ применяются механические колебательные системы, из которых наиболее широкое распространение получили кварцевые резонаторы (КвР). Существование прямого и обратного пьезоэлектрического эффектов в кварце, допускающих практически полное преобразование электрической энергии в механическую и обратно, делает удобным использование КвР в качестве колебательной системы АГ. В кварцевых резонаторах может быть возбуждено несколько видов механических колебаний, а в пределах данного вида возможны колебания на основной частоте и на механических гармониках. Поэтому электрическая эквивалентная схема КвР (рис.1.2,а) может быть представлена в виде параллельного соединения емкости кварцедержателя C0 и, в общем случае, бесконечного числа LквCквRкв-контуров, резонансные частоты которых совпадают с частотами механических колебаний кварцевой пластины. Так как КвР является высокодобротной колебательной системой, при построении эквивалентной схемы, справедливой для узкого диапазона, вблизи каждой из частот гармоник можно пренебречь влиянием всех последовательных контуров, кроме одного, настроенного на эту частоту. 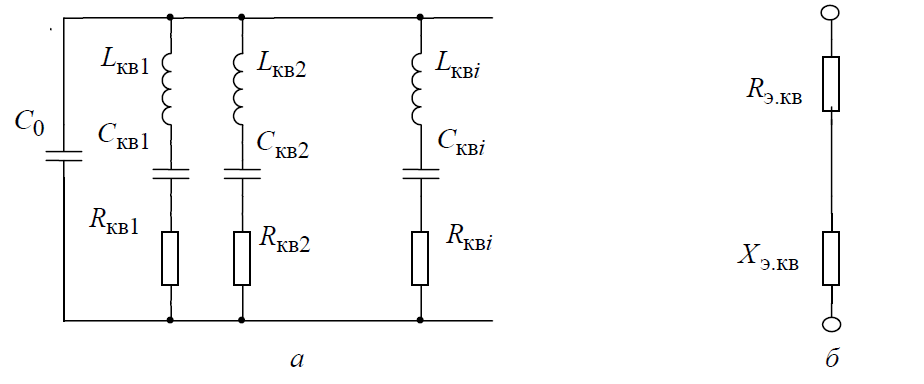 Рис. 1.2 К основным параметрам эквивалентной схемы КвР, приводимым в справочных данных, относятся: динамические индуктивность Lкв и емкость Cкв, емкость кварцедержателя C0, сопротивление потерь Rкв, добротность резонатора 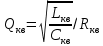 и частота последовательного резонанса в динамической ветви и частота последовательного резонанса в динамической ветви 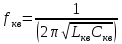 . .При анализе и проектировании кварцевых АГ кварцевый резонатор удобно представить в виде последовательного соединения резистивного Rэ.кв и реактивного Xэ.кв двухполюсников (рис.1.2,б), т. е. Zэ.кв=Rэ.кв+jXэ.кв, где 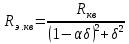 ; (1.10) ; (1.10)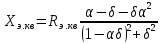 . (1.11) . (1.11)Здесь =Qкв(1–fкв2/f2)2Qкв(f–fкв)/fкв – обобщенная расстройка; =2fквRквC0. Таблица 1.2 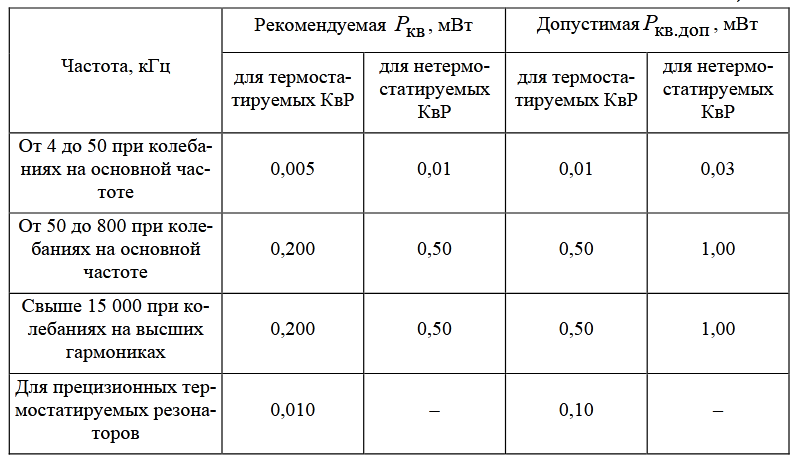 Анализ выражения (1.11) показывает, что эквивалентное сопротивление резонатора носит индуктивный характер в диапазоне относительных расстроек от δ до (1/δ−δ). За пределами этой области КвР имеет емкостный характер эквивалентного сопротивления. Крутизна фазочастотной характеристики КвР с учетом (1.10) и (1.11): 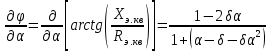 достигает максимального значения, равного 1 (∂/∂α=2Qкв/fкв) при α = 0. При α=0,76 ∂/∂α падает в 2 раза, а при α=0,95 – в 3 раза, что необходимо учитывать при выборе резонатора, исходя из заданной частоты генерируемых колебаний. Характерным свойством КвР является старение, приводящее к необратимому изменению резонансной частоты fкв. Скорость старения максимальна в начале срока эксплуатации резонатора и пропорциональна рассеиваемой в нем мощности. Поэтому КвР первоначально подвергают «тренировке», т. е. работе с повышенной мощностью рассеивания (Pкв). При дальнейшем использовании Pкв должна соответствовать значениям, указанным в табл.1.2. В табл.1.3 приведены основные параметры некоторых типов резонаторов. Таблица 1.3 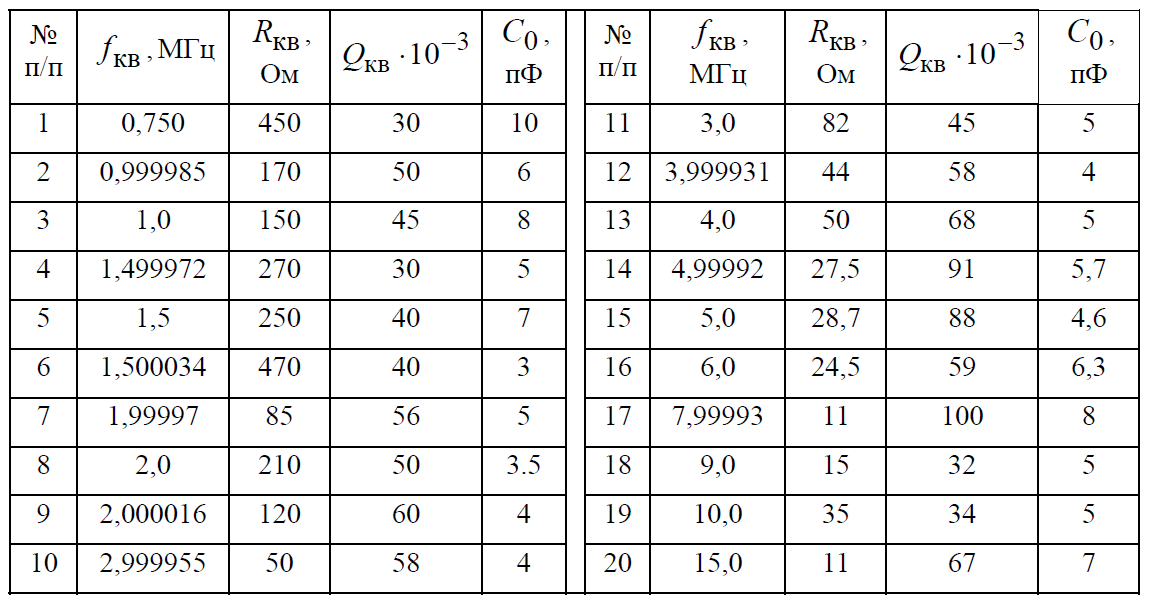 Серийно выпускаемые КвР изготавливаются на частоты от 4кГц до 100МГц в различном конструктивном исполнении: вакуумированные, герметизированные, миниатюрные и микромодульные. Допустимые относительные отклонения частоты настройки резонаторов от номинального значения в зависимости от класса резонатора лежат в пределах ±0,510−6...±5010−6. Долговременная относительная нестабильность частоты вакуумированных КвР составляет (3...5)10−6, а герметизированных – (10...30)10−6. Относительная нестабильность за сутки не превышает 10−10. До 15МГц кварцевые резонаторы возбуждаются на основной частоте, а свыше 15МГц – на гармониках. 1.3.2. Сравнительная характеристика основных схем кварцевых автогенераторов Широко используемые на практике схемы автогенераторов с кварцевой стабилизацией, несмотря на их многообразие, можно разбить на две большие группы. К первой группе схем относятся те, в которых КвР включается вместо одного из двухполюсников Z1, Z2 или Z3 в обобщенной трехточечной схеме АГ (рис.1.3). Это так называемые осцилляторные схемы. В них эквивалентное сопротивление КвР должно носить индуктивный характер, а выход резонатора из строя приводит к срыву колебаний, поскольку невозбужденный КвР имеет емкостный характер эквивалентного сопротивления. В осцилляторных схемах частота генерации fг удовлетворяет условию fкв ≤ fг ≤ fп, где fп – частота параллельного резонанса. 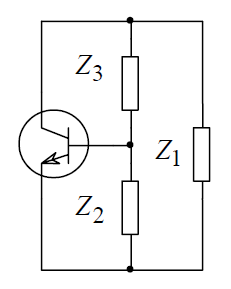 Рис. 1.3 Из осцилляторных схем наибольшее практическое применение находит схема с КвР между коллектором и базой транзистора, построенная на основе емкостной трехточечной схемы, или схемы Клаппа. Высокая стабильность частоты этих схем обусловлена как меньшим шунтированием КвР самим транзистором, так и тем, что высшие гармоники в базовом и коллекторном напряжениях ослабляются конденсаторами C1 и C2. Последнее препятствует дополнительному увеличению фазового угла средней крутизны. Oдна из возможных схем такого АГ приведена на рис.1.4. 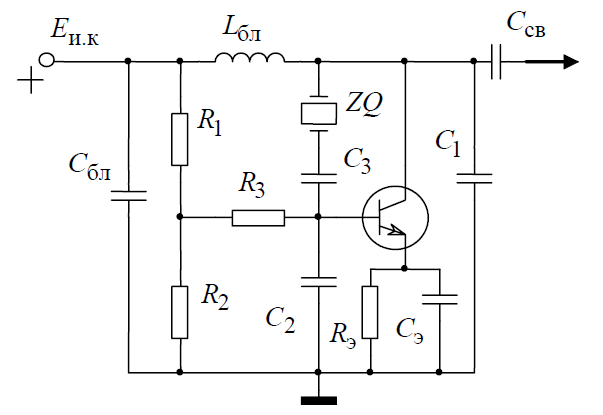 Рис. 1.4 Во вторую группу схем можно включить схемы с КвР в цепи обратной связи и схемы с КвР в контуре. Во всех этих схемах, как правило, помимо КвР имеется обычный колебательный контур, обеспечивающий выполнение условий самовозбуждения. Отличительной особенностью схем второй группы является то, что в них КвР используется как высокодобротный последовательный контур. Схемы с кварцем в цепи обратной связи могут быть получены из схемы на рис.1.3 при включении КвР в одну из ветвей, соединяющих колебательный контур с эмиттером или базой транзистора, а схемы с кварцем в контуре – включением КвР последовательно с одним из двухполюсников Z1, Z2 или Z3. В обеих схемах генерация происходит на частотах, близких к частоте fкв. И в том и в другом случае за основу берется емкостная трехточечная схема, позволяющая получить наибольшую стабильность частоты. Один из широко применяемых вариантов схемы с КвР в цепи обратной связи представлен на рис.1.5, а схемы с КвР в контуре – на рис.1.6. 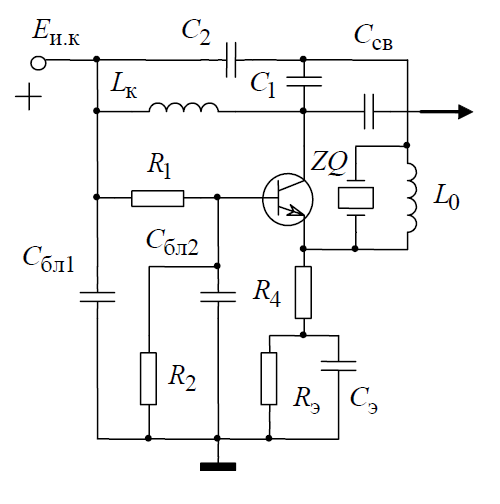 Рис. 1.5 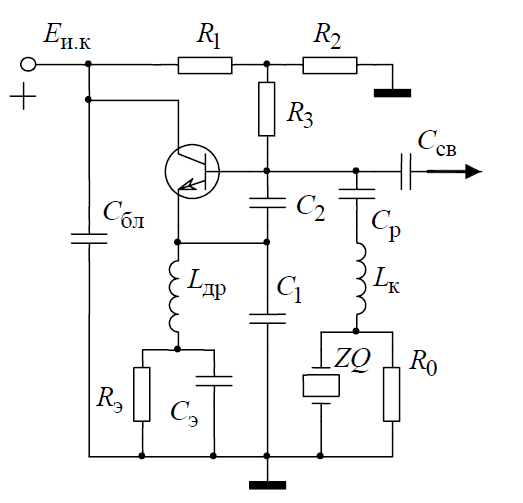 Рис. 1.6 Схема на рис.1.4 обладает наибольшей стабильностью частоты, но может быть использована только при работе на основной частоте. Кроме того, в ней, как уже указывалось, частота генерации должна быть несколько выше, чем fкв. Схемы на рис.1.5 и 1.6 могут применяться как при работе на основной частоте, так и на высших механических гармониках. Частота генерируемых колебаний должна лежать в достаточно узкой окрестности частоты fкв. В схемах второй группы принципиально возможно возбуждение колебаний нестабилизированных КвР за счет шунтирующего действия емкости кварцедержателя C0. Для подавления таких колебаний резонатор шунтируется либо резистором R0, значение которого определяется соотношением R0=1/(2πfквC0), либо катушкой индуктивности L0. Ее номинал выбирается из условия 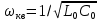 , где ωкв=2πfкв. Нестабильность частоты, обусловленная изменением параметров транзистора и колебательной системы, в АГ, выполненном по схеме на рис.1.5, ниже, чем в схеме на рис.1.6. , где ωкв=2πfкв. Нестабильность частоты, обусловленная изменением параметров транзистора и колебательной системы, в АГ, выполненном по схеме на рис.1.5, ниже, чем в схеме на рис.1.6.Выходная мощность автогенераторов, построенных по схемам на рис.1.4 и 1.6, обычно не превышает 0,1...0,5мВт, а по схеме на рис.1.5 – 1...5мВт. Нестабильность частоты, вызванная изменением температуры окружающей среды, во всех АГ обусловлена КвР и практически одинакова. 1.3.3. Расчет автогенератора с кварцевым резонатором между коллектором и базой транзистора Цель расчета – определение параметров колебательной системы АГ (емкостей конденсаторов C1, C2 и C3) в схеме на рис.1.4, режима работы транзистора и элементов цепей питания, при которых обеспечивается заданная частота генерируемых колебаний и наибольшая ее стабильность, а мощность, рассеиваемая КвР, не превышает допустимую. Исходным при расчете является комплексное уравнение стационарного режима: S1(coss+jsins)Zу =1, где S1=S1.0coss, S1.0=S011−cos)– средняя крутизна транзистора по первой гармонике; Zу =−Z1Z2/(Z1+Z2+Z3+Zэ.кв), Z1≈−jX1, Z2≈−jX2, Z3≈−jX3, которое после разделения на мнимую и вещественную составляющие дает следующую систему уравнений: Rквtgs=Xэ.кв −Xк; (1.12) S1 coss X1X2=Rэ.кв; (1.13) г=2Qкв(fг −fкв)/fкв, (1.14) где αг – обобщенная расстройка КвР; Xэ.кв=Rквαг; Xк = X1+X2+X3=1/(ωгCк) – полное сопротивление емкостной ветви контура; Cк – полная емкость контура; X1=1/(ωгC1); X2=1/(ωгC2 ); X3=1/(ωгC3). Относительное изменение частоты, вызванное изменениями параметров колебательной системы и транзистора, определяется соотношением: 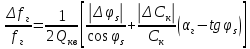 , (1.15) , (1.15)где Δsи ΔCк – абсолютные приращения sи Cк, обусловленные действием дестабилизирующих факторов. Расчет АГ начинается с выбора кварцевого резонатора. При этом необходимо руководствоваться следующими соображениями. Резонансная частота fкв должна быть несколько ниже fг, т.е. αг>0. При этом чем меньше αг, тем в меньшей степени будут влиять параметры колебательной системы на частоту генерируемых колебаний (см.(1.15)). Однако, как это следует из соотношения (1.12), малым значениям αг соответствуют большие значения Cк, при которых затрудняется выполнение условия (1.13), являющегося уравнением баланса амплитуд в АГ. Оптимальные значения αг обычно лежат в пределах 0,5…3. Если имеется несколько резонаторов с требуемой частотой, предпочтение следует отдать КвР с большей добротностью и меньшим значением Rкв. Далее, в соответствии с рекомендациями, изложенными в п.1.1, выбирается тип транзистора и режим его работы, т.е. определяются β0, S0, Sгр, s, Eк, Eб0, iкm, θ, Iк1, Iк0. Основное внимание при выборе транзистора следует обратить на возможность обеспечения малого значения фазового угла средней крутизны, во многом определяющего в соответствии с (1.15) влияние на fг параметров транзистора и Cк. Кроме того, желательно иметь возможно большие значения крутизны коллекторного тока S0 при iкm, удовлетворяющем (1.1). После выбора транзистора и КвР с помощью соотношения (1.14) определяется обобщенная расстройка αг, находится Xкв, а затем, пользуясь уравнениями баланса амплитуд (1.13) и фаз (1.12), рассчитываются Xк и X1X2. Далее по известному значению амплитуды первой гармоники коллекторного тока Iк1 определяется требуемое значение амплитуды напряжения на базе Uб1 = Iк1/S1 и, считая, что ток в контуре существенно больше базового тока транзистора, устанавливается связь между током, протекающим через кварцевый резонатор Iкв, и напряжением на базе, т.е. Uб/Iкв = X2. Для определения тока Iкв, входящего в последнее соотношение, достаточно учесть, что 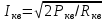 , где Pкв – мощность, рассеиваемая на КвР, значением которой следует задаться в соответствии с рекомендациями табл.1.2. , где Pкв – мощность, рассеиваемая на КвР, значением которой следует задаться в соответствии с рекомендациями табл.1.2.Таким образом, становятся известными X1X2, X2 и Xк, т.е. сопротивления всех конденсаторов, входящих в состав колебательной системы АГ. Если в результате расчета оказывается, что X1+X2>Xк (это означает, что баланс фаз в АГ реализовать не удается), следует уменьшить Pкв по сравнению с ранее выбранным. По известным значениям X1, X2, X3 и ωг определяются емкости соответствующих конденсаторов. Поскольку стандартные значения емкостей несколько отличаются от расчетных, их номиналы выбираются таким образом, чтобы получить заданное значение Cк(Xк). Точно установить частоту генерации можно с помощью подстроечного конденсатора, подключаемого параллельно наименьшей из емкостей контура. Попутно отметим, что при выборе типа конденсаторов целесообразно отдать предпочтение тем, которые имеют наименьшее значение ТКЕ. На этом расчет колебательной системы автогенератора заканчивается, после чего определяются токи и напряжения в схеме АГ, проводится энергетический расчет и вычисляются номиналы элементов цепей питания. Выбор питающих напряжений, расчет цепей питания, номиналов блокировочных и разделительных элементов производятся на основании рекомендаций, изложенных в п.1.2 (см.(1.1) – (1.9)). Пример расчета Рассчитать параметры и режим работы кварцевого АГ, работающего на частоте 3МГц. Параметры выбранного биполярного транзистора: β0=50; fт=500МГц; Sгр=0,05А/В; Eб0=0,25В; rб=60Ом; Eк.доп=12В; Iк.доп=0,05А; Pк.доп=0,15Вт. 1. В соответствии с изложенными рекомендациями задаемся iкm=0,007А, θ=80° (α1=0,472, α0=0,286) и определяем S0=0,093A/B; S1.0=0,036A/B; fs=89,6МГц; s=−1,91°; S1≈S1.0=0,036A/B; Iк1=0,0033A. 2. Выбираем кварцевый резонатор со следующими параметрами: fкв=2,99995МГц; Rкв=50Ом; Qкв=50000 и задаемся мощностью, рассеиваемой резонатором Pкв=0,0003Вт<Pкв.доп=0,0005Вт. Расчет параметров колебательной системы АГ 1. Обобщенная расстройка αг=2Qкв(fг − fкв)/fкв = 250000(3−2,99995)/3=1,67. 2. Реактивное сопротивление кварцевого резонатора на частоте генерации Xэ.кв=Rквαг=501,67 = 83,5 Ом. 3. Полное реактивное сопротивление емкостной ветви контура X к=Xк=Xэ.кв−Rквtgs=83,5+500,033=85,17Ом. 4. Произведение X1X2=Rкв/(S1 coss)=50/(0,0360,999)=1389,7Ом2. 5. Амплитуда первой гармоники тока через кварцевый резонатор: 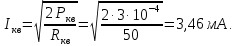 6. Амплитуда первой гармоники напряжения на базе транзистора: Uб=Iк1/S1=0,0033/0,036=0,092B. 7. Cопротивление конденсатора C2: X2=Uб/Iкв=0,092/0,00346=26,5Ом. 8. Сопротивление конденсатора C1: X1=X1X2/X2=1389,7/26,5=52,44Ом. 9. Сопротивление конденсатора C3: X3=Xк−X1–X2=85,17−52,44−26,5=6,23Ом. 10. Емкости конденсаторов колебательной системы: C1 = 1/(2πfг X1) = 1/(2π310632,4)=1012 пФ; C2 = 1/(2πfг X2)= 1/(2π310626,5)=2002 пФ; C3 = 1/(2πfг X3)= 1/(2π31066,23)=8515 пФ; Расчет режима работы транзистора 1. Амплитуда напряжения на коллекторе: 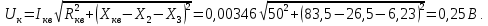 2. Постоянное напряжение на коллекторе транзистора: Eк=0,3Eк.доп =0,3⋅12=3,6В. 3. Проверка недонапряженного режима работы: Uк.гр=Eк−iкm/Sгр=3,6−0,007/0,05=3,46B. 4. Модуль эквивалентного сопротивления колебательного контура: Zэк =Uк/Iк1=0,25/0,0033=75,8Ом. 5. Мощность, потребляемая транзистором от источника коллекторного напряжения: P0=Eк iкmα0=3,460,0070,286=0,00693Вт. 6. Мощность, рассеиваемая на коллекторе транзистора: Pк=P0−Pкв=0,00693−0,0003=0,00663Вт. 7. Коэффициент полезного действия транзистора: η=Pкв/P0=0,3/6,93=0,043. 8. Постоянная составляющая тока базы: Iб0=iкmα0/β0=0,0070,286/50=0,04мA. 9. Напряжение смещения на базе: Eб=−Uб cosθ+Eб0=−0,0920,174+0,25=0,234В. Расчет элементов цепей питания 1. Индуктивность дросселя в цепи коллекторного питания: Lдр=(20…30)Zэк/ωг=2575,8/(2π3106)=100,6мкГн. Часто, с точки зрения технологичности целесообразно заменить дроссель балластным резистором Rб, сопротивление которого выбирается из аналогичного условия, т.е. Rб=(20...30)Zэк. 2. Напряжение источника коллекторного питания Eи.к=Eк+(Iк0+Iб0)Rэ, где Rэ определяется из соотношения (1.3). В том случае, когда вместо дросселя используется балластный резистор, при вычислении Eи.к необходимо учесть падение напряжения на нем. Цепи базового автосмещения рассчитываются на основе соотношений (1.6) – (1.8), а Cэ выбирается из условия Iк1/(ωгCэ)=Uб/(20...30). |
